Complete Solutions to Examples of chapter STRAIGHT LINES of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | STRAIGHT LINES |
| NEW JOYTHI PUBLICATION | Examples |
| Number Of Questions | 90 |
| Academic Year | 2023-24 |
Find the slope of the straight line through (-3, 2) and (3, 3).
View SolutionFind whether the line through (-3, 2) and (3, 3) is perpendicular or parallel or neither perpendicular nor parallel to the line through (-2, -1) and (4, 0).
View Solutioni. Find the slope of the line joining (-2,6) and (4,8).
ii. Find the value of x, if the above line is perpendicular to the line joining (8, 12) and (x, 24).
View SolutionThe vertices of `Delta ABC` are A(2,4) B(-4, 2) and C(0,0). Find the slopes of AC and AB.
View SolutionFind the angle between x-axis and the line joining (2,-1) and (4, -3).
View SolutionThe slope of a line is double of the slope of another line. Iftangent of the angle between them `(1)/(3)`, find the slopes of the lines.
View SolutionIf the angle between two lines is `(pi)/(4)` and slope of one of the lines is `(1)/(2)`, find the slope of the other line.
View SolutionFind the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points P(0, -4) and B(8, 0).
View SolutionFor what value of x, the points (x,-1), (2, 1) and (4,5) are collinear?
View SolutionIf three points `A(h ,0),\ P(a , b)a n d\ B(0, k)` lie on a line, show that: `a/h+b/k=1.`
View SolutionConsider the following population and year graph. Find the slope of the line AB and using it, find what will be the population in the year 2010?
View SolutionDraw a quadrilateral in the Cartesian plane, whose vertices are (-4,5), (0,7), (5,-5) and (-4,-2). Also, find its area.
View SolutionThe base of an equilateral triangle with side 2a lies along the y-axis such that the mid-point of the base is at the origin. Find vertices of the triangle.
View SolutionFind the distance between P(`x_(1), y_(1)`) and Q(`x_(2), y_(2)`) when :
i. PQ is parallel to the y-axis, ii. PQ is parallel to the x-axis.
View SolutionFind a point on the x-axis, which is equidistant from the points (7,6) and (3, 4).
View SolutionFind the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points P(0, -4) and B(8, 0).
View SolutionWithout using the Pythagoras theorem, show that the points (4,4), (3, 5) and (-1,-1) are the vertices of a right angled triangle.
View SolutionFind the slope of the line, which makes an angle of `30^(@)` with the positive direction of y-axis measured anticlockwise.
View SolutionWithout using distance formula, show that points `(-2, -1) , (4, 0) , (3, 3) " and " (-3, 2)` are the vertices of a parallelogram.
View Solution. Find the angle between the x-axis and the line joining the points `(3, -1) " and " (4, -2)` .
View SolutionA line passes through (`x_(1), y_(1)`) and (h, k). If slope of the line is m, show that `k-y_(1) = m(h-x_(1))`.
View SolutionFind the equation of a straight line passing through (-5,7) and parallel to the x - axis.
View SolutionFind the equation of the line which is parallel to y-axis and passing through the point (3,4).
View SolutionFind the equation of the line passing through the point (-2, 3) with slope - 4.
View SolutionFind the equation of a line through the origin which makes an angle of `45^(@)` with the positive direction of x-axis.
View SolutionConsider the line joining the points (2, - 1) and (6, – 3).
i. Find its slope.
ii. Find the equation of the perpendicular bisector.
View SolutionThe vertices of triangle ABC are A (-2, 3), B (2, -3) and C (4,5)
i. Find the slope of BC.
ii. Find the equation of the altitude of triangle ABC passing through A.
View SolutionWrite the equation of the line through the points (1,-1) and (3,5)
View SolutionFind the equation of the line intersecting x-axis at a distance of 3 units to the left of the origin with slope `-2`.
View SolutionFind the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point (2, 3).
View SolutionFind the equation of the line which passes through the point (3, 4) and whose intercepts on the axes are equal in magnitude but opposite in sign.
View SolutionFind the equation of the line through the point (3, 3) and cutting off intercepts on the axes whose sum is 12.
View SolutionFind the equation of the line which has the length of the perpendicular from origin to the line as 4 units and the perpendicular segment on the line I makes an angle of `120^(@)` with the positive direction of x-axis.
View SolutionIn the figure given below, find the equation of the line AB.
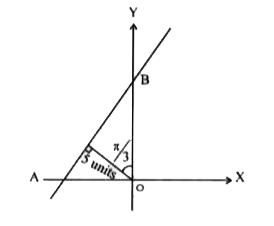
View SolutionBy using the concept of equation of a line, prove that the three points (3,0), (-2, - 2) and (8, 2) are collinear.
View SolutionIntersecting the y-axis at a distance of 2 units above the origin and making an angle of `30^(@)` with positive direction of the x-axis.
View SolutionFind the equation of line which is at Perpendicular distance from the origin is 5 units and the angle made by the perpendicular with the positive x-axis is `30^(@)`.
View SolutionFind the equation of the line passing through (-3, 5) and perpendicular to the line through the points (2,5) and (-3, 6).
View SolutionA line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1: n. Find the equation of the line.
View SolutionFind equation of the line through the point(0, 2) making an angle `(2pi)/(3)` with the positive x-axis. Also, find the equation of line parallel to it and crossing the y-axis at a distance of 2 units below the origin.
View SolutionThe perpendicular from the origin to a line meets it at the point `(-2, 9)` find the equation of the line.
View SolutionThe length L (in centimetrs) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124.942 when C = 20 and L= 125.134 when C = 110, express L in terms of C.
View SolutionThe owner of a milk store finds that, he can sell 980 litres of milk each week at Rs. `14 // "litre"` and 1220 litres of milk each week at Rs `16 // "litre"`. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs `17 // "litre"`?
View SolutionP (a, b) is the mid-point of a line segment between axes. Show that equation of the line is `(x)/(a)+(y)/(b)=2`
View SolutionPoint R (h, k) divides a line segment between the axes in the ratio 1: 2. Find equation of the line.
View SolutionConvert the equation of the line 2x – 3y +6=0 into intercept form.
View SolutionThe equation of a straight line is 3x - 4y + 10 = 0.
Find
i. slope-intercept form
ii. slope
iii. x and y intercepts.
View SolutionConsider the points A(2,3) and B (4,5)
i. Find the slope of the line passing through the points A and B.
ii. Find the equation of the line passing through A and B.
iii. Find the x-intercept of the above line.
View SolutionReduce the equation of the line `sqrt(3)x + y-8 = 0` into normal form. Find the values of p and `omega`.
View Solutioni. Find the point of intersection of the lines 2x +y-3=0, 3x-y-2=0
ii. Find the equation of the line passing through the above point of intersection and parallel to the line x + y + 1 = 0.
View SolutionFind equation of the line perpendicular to the line x - 7y + 5 = 0 and having x - intercept 3.
View SolutionConsider the straight line 3x + 4y + 8 = 0
i. What is the slope of the line which is perpendicular to the given line?
ii. If the perpendicular line passes through (2,3), form its equation,
iii. Find the foot of the perpendicular drawn from (2,3) to the given line.
View SolutionConsider the points A(-2, -3) and B(1,6).
i. Find the equation of the line passing through A and B.
ii. Find the equation of the line passing through (2, 1) and perpendicular to AB
iii. Find the foot of the above perpendicular to AB.
View SolutionConsider the points A(2, 2) and B(5,3).
i. Find the slope of the line through, the points A and B.
ii. Find the equation of the line passing through the points A and B.
iii. Find the image of the point(1, 2) in the line through A and B.
View SolutionFind the distance of the point (3,-3) from the line 3x - 4y - 26 = 0
View SolutionConsider the line 3x – 4y + 2 = 0 and the point (2, -3)
Find the distance of the point from the line.
View SolutionFind the distance between the parallel lines 3x – 4y + 5 = 0 and 3x – 4y + 7 = 0
View Solutioni Reduce the equation 3x + 4y - 12 = 0 into intercept form.
ii. Find the distance of the above line from the origin.
iii. Find the distance of the above line from the line 6x + 8y- 18 = 0.
View SolutionWhat are the points on the y-axis whose distance from the line `(x)/(3)+(y)/(4)=1` is 4 units.
View SolutionFind the distance between parallel lines
i. 15x+8y-34= 0 and 15x+8y+31=0
ii. l(x + y) + p = 0 and l(x + y) - r = 0.
View SolutionFind angles between the lines `sqrt3x + y = 1 " and " x + sqrt3y = 1`.
View SolutionTwo lines passing through the point (2, 3) intersects each other at an angle of `60^(@)`. If slope of one line is 2, find equation of the other line.
View SolutionFind the equation of the right bisector of the line segment joining the points `(3, 4) " and " (-1, 2)`.
View SolutionFind the coordinates of the foot of perpendicular from the point `(-1, 3)` to the line `3x - 4y - 16 = 0 `.
View SolutionThe perpendicular from the origin to the line y = mx + c meets it at the point `(-1, 2)`. Find the values of m and c.
View SolutionIf p and q are the lengths of perpendiculars from the origin to the lines `x cos theta - y sin theta = k cos 2 theta " and " x sec theta + y cosec theta = k `, respectively, prove that `p^(2) + 4q^(2) = k^(2)`.
View SolutionIn the triangle ABC with vertices `A (2, 3) , B (4, -1) " and " C (1, 2)`, find the equation and length of altitude from the vertex A.
View SolutionABC is a right triangle right angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB. Prove that (i) pc = ab (ii) `(1)/(p^(2)) = (1)/(a^(2)) + (1)/(b^(2))` .
View SolutionFind the value of `alpha` and p if the equation `xcosalpha+ysinalpha=p` is the normal form of the line `sqrt(3x)+y+2=0`.
View SolutionFind the equations of the lines, which cut-off intercepts on the axes whose sum and product are 1 and -6, respectively.
View SolutionWhat are the points on the y-axis whose distance from the line `(x)/(3)+(y)/(4)=1` is 4 units.
View SolutionFind perpendicular distance from the origin of the line joining the points (`cos theta, sin theta`) and (`cos phi, sin phi`).
View SolutionFind the equation of the line parallel to y-axis and drawn through the point of intersection of the lines `x - 7y + 5 = 0 " and " 3x + y = 0 `.
View SolutionFind the equation of a line drawn perpendicular to the line `x/4 + y/6 = 1` through the point , where it meets the y-axis.
View SolutionFind the area of the triangle formed by the lines `y - x = 0, x + y = 0 " and " x - k = 0 `.
View SolutionIf three lines whose equations are `y = m_(1) x + c_(1) , y = m_(2) x + c_(2) " and " m_(3) x + c_(3) ` are concurrent, then show that `m_(1) (c_(2) - c_(3)) + m_(2) (c_(3) - c_(1)) + m_(3) (c_(1) - c_(2)) = 0 `.
View SolutionFind the equation of the lines through the point (3, 2) which make an angle of `45^(@)` with the line `x - 2y = 3`.
View SolutionFind the equation of the line passing through the point of intersection of the lines 4x + 7y - 3 = 0 and 2x – 3y + 1 = 0 that has equal intercepts on the axes.
View SolutionShow that the equation of the line passing through the origin and making an angle `theta " with the line " y = mx + c " is " y/x = (m pm tan)/(1 pm m tan)`.
View SolutionIn what ratio, the line joining `(-1, 1) " and " (5, 7)` is divided by the line `x + y = 4 ?`
View SolutionFind the distance of the line `4x + 7y + 5 = 0 ` from the point `(1, 2)` along the line `2x - y = 0`.
View SolutionFind the direction in which a straight line must be drawn through the point `(-1, 2)` so that its point of intersection with the line `x + y = 4` may be at a distance of 3 units from this point.
View SolutionThe hypotenuse of a right angled triangle has its ends at the points `(1, 3) " and " (-4, 1)`. Find an equation of the legs (perpendicular sides) of the triangle.
View SolutionFind the image of the point (3,8) with respect to the line x+3y = 7 assuming the line to be a plane mirror.
View SolutionIf the lines `y = 3x + 1 " and " 2y = x + 3` are equally inclined to the line `y = mx + 4`,find the value of m.
View SolutionIf sum of the perpendicular distances of a variable point P(x, y) from the lines x+y-5= 0 and 3x - 2y +7=0 is always 10. Show that P must move on a line.
View SolutionFind equation of the line which is equidistant from parallel lines `9x + 6y - 7 = 0 " and " 3x + 2y + 6 = 0 `.
View SolutionAray of light passing through the point(1, 2) reflects on the x-axis at point A and the reflected ray passes through the point (5,3). Find the coordinates of A.
View SolutionProve that the product of the lengths of the perpendiculars drawn from the points `(sqrt(a^(2)-b^(2)), 0)` and `(-sqrt(a^(2)-b^(2)), 0)` to the line `(x)/(a)cos theta+(y)/(b)sin theta=1` is `b^(2)`
View SolutionA person standing at the junction (crossing) of two straight paths represented by the equations 2x-3y+4= 0 and 3x + 4y-5=0 wants to reach the path whose equation is 6x – 7y+8=0 in the least time. Find equation of the path that he should follow.
View Solution
Examples questions and complete solutions for chapter STRAIGHT LINES of NEW JYOTHI MATHS (TAMIL ENGLISH) of Class 12