Complete Solutions to EXAMPLES of chapter RELATIONS AND FUNCTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| NEW JOYTHI PUBLICATION | EXAMPLES |
| Number Of Questions | 91 |
| Academic Year | 2023-24 |
If `P = {4,3,2} and q={5} `, form the sets `P xx Q and Q xx P` are these two products equal ?
View Solutionif `A xx B ={(1,3)(1,5)(2,3)(2,5)(3,3)(3,5)}`
`I . ` find A and B
ii. Find `A xx A`
View SolutionLet A and B are two sets such that n(A) = 3 and n(B) =2 . If (x,1) , (y,2) and (z,1) are in `A xx B` , find A and B where x,y, z are distinct elements.
View SolutionLet `A = {1,2} ,B = {1,2 ,3,4 } ,c={5,6} and d={5,6,7,8 } ` verify that
`A xx ( B nn C ) = (A xx B ) nn (A xx C ) `
View SolutionLet `A = {1,2} ,B = {1,2 ,3 } ,c={5,6} and d={5,6,7 } ` verify that
`A xx C ` is a subset of `B xx D `
View SolutionIf `(x/3+1, y-5/3) =(7/3,1/3)` , find the values of x and y.
View SolutionIf `A ={-1,1} ,` find `A xx A xxA `
View SolutionIf `A xxB = {(a , x), (a , y), (b , x), (b , y)}`. Find A and B.
View SolutionThe cartesian product `A xx A ` has 9 elements among which are found (-1,0) and (0,1) . Find the set A and the remaining elements of `A xx A `
View SolutionLet `A={1,2,3} and B ={a,b}`
write the universal relation from A to B .
View SolutionLet `A={1,2,3} and B ={a,b}`
what is the number of non empty relations from A to B
View SolutionLet `A ={2,3},B={4,6} .` let R be relation on A defined by
`R ={(A,b),a in A,b in B , a ` divides b}
find ` A xx B ` and the number of relations from A to B .
View SolutionLet `A ={2,3},B={4,6} .` let R be relation on A defined by
`R ={(a,b),a in A,b in B , a ` divides b}
find the domain and range of R .
View SolutionLet `A= {1,2,3,4 }` and R be relation on A defined by
R ={(a,b) : a,b,`in` A,B is exactly divisible by a }
write R in the roster form .
View SolutionLet `A= {1,2,3,4,6 }` and R be relation on A defined by
R ={(a,b) : a,b,`in` A,b is exactly divisible by a }
write the domain and range of R
View SolutionLet `A={ 1,2,3,4} , B={1,4,5}` be two sets . If R is the relation `'' lt '' ` from A to B , then
Write R in roster form
View SolutionLet `A={ 1,2,3,4} , B={1,4,5}` be two sets . If R is the relation `'' lt '' ` from A to B , then
Write the domain and range of R.
View SolutionLet `A={ 1,2,3,4} , B={1,4,5}` be two sets . If R is the relation `'' lt '' ` find cartestian equation and r inverse.
View SolutionThe figure shows a relation between the sets P and Q
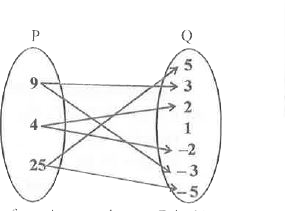
write this relative (I ) in set - builder form
(ii ) in roster form
View SolutionThe figure shows a relation between the sets P and Q
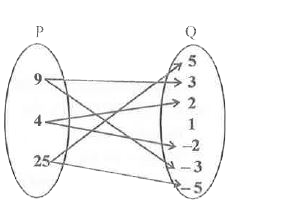
write its domain and range
View SolutionThe set A contains 3 elements and the number of relation from A to another set B is 64.
find the number of elements in B .
View SolutionLet `A ={1,2,3,…… 14 }` R is a relation on A defined by `R = {(x,y),3x -y=0 ,x,y in A }`
write R in tabular form
View SolutionLet `A ={1,2,3,…… 14 }` R is a relation on A defined by `R = {(x,y),3x -y=0 ,x,y in A }`
find the domain , and range or R .
View Solutionconsider the relation `R ={ (x,2x -1 ) |x in A }, ` where `A = { 1,-1,3 }`
write R in roster form
View Solutionconsider the relation `R ={ (x,2x -1 ) |x in A }, ` where `A = { 1,-1,3 }`
write the range of R .
View SolutionDetermine the domain and range of the relation R where `R = { (x,x ^3) : x` is a prime number less than 15 }.
View SolutionLet A ={1,2,3,4,5,6} . Define a relation R from A to A by `R = {(x,y):y =x+1}`
Depict this relation using an arrow diagram .
View SolutionLet A ={1,2,3,4,5,6} . Define a relation R from A to A by `R = {(x,y):y =x+1}`
write down the domain , and range of R .
View SolutionLet A ={ 1,2,3,4,5} and R be the relation on A defined by `R= {(a,b}: b=a^2}`
write R in roster form
View SolutionLet A ={ 1,2,3,4,5} and R be the relation on A defined by `R= {(a,b}: b=a^2}`
find the range of R.
View SolutionThe cartesian product `P xxP` has 9 elements among which are found `(-a,0) and (0,a)`
A relation from P to P is defined as R `={ (xy): x+y =0}`
How many relations are possible from P to P ?
View SolutionThe cartesian product `P xxP` has 9 elements among which are found `(-a,0) and (0,a)`
A relation from P to P is defined as R `={ (xy): x+y =0}`
How many relations are possible from P to P ?
View SolutionThe cartesian product `P xxP` has 9 elements among which are found `(-a,0) and (0,a)`
A relation from P to P is defined as R `={ (xy): x+y =0}`
How many relations are possible from P to P ?
View SolutionA ={ 1,2,3,5} and B={ 4,6,9 } . Define a relation R from A to B by R `= {( x,y) }` : the difference between x and y is odd `, x in A , y in B `} write R in roster form
View SolutionThe figure shows a relationship between the sets P and Q . Write the relation
roster form
View SolutionThe figure shows a relationship between the sets P and Q . Write the relation
in set- builder form
View SolutionThe figure shows a relationship between the sets P and Q . Write the relation
what is its domain and range ?
View SolutionWrite the relation `R={ (x,x^3) "x` is a prime number less than 10 } in roster form
View SolutionExamine each of the following relations given below and state in each case giving reasons whether it is a function ir not ?
` R={(2,1,) ,( 3,1),( 4,2)}`
View SolutionExamine each of the following relations given below and state in each case giving reasons whether it is a function ir not ?
`R={(2,2),(2,4),(3,3) ,(4,4)}`
View SolutionExamine each of the following relations given below and state in each case giving reasons whether it is a function ir not ?
`R={(1,2,(2,3),(3,4 ),(4,5) ,(5,6),(6,7)}`
View SolutionGiven `A= {3,4,5} b={2}`
the number of relation from A to B is _____
View SolutionGiven `A= {3,4,5}. determine the domain and range of relation Ria defined as ` R= {(x,y)| y=x-2}`
View SolutionGiven `A= {3,4,5} b={2}`
Represent the above relation R using an arrow diagam
View SolutionGiven `A= {3,4,5} b={2}`
the number of relation from A to B is _____
View SolutionLet N be the set of natural numbers and the relation R be defined on N such that `R={(x,y): y=2x,x,y in N }.`
what is the domain codomain and range of R ? Is this relation a functions ?
View SolutionConsider the real function f(x) =1 -2x
find f(-1) and f(2)
View SolutionConsider the real function f(x) =1 -2x
find x if f(x) =-1
View Solutionconsider the real function of `f(x ) =(x^2 +2x +3)/( x^2 -8x +12)`
find the value of x if f (x ) =1
View Solutionconsider the real function of `f(x ) =(x^2 +2x +3)/( x^2 -8x +12)`
find the domain of f .
View SolutionFind the domain of the function `f(x) = (x^2 + 3x +5 )/( x^2 -5x+4)`
View SolutionLet ` f={(1,1 ) ,(2,3),(0,-1) ,(-1,-3) }` be a function from Z to Z defined by f(x) =ax + b for some integers a , b, determine a,b.
View SolutionConsider the real function `f(x ) = ( x+2)/( x-2)`
find the domain and range of the function
View SolutionConsider the real function `f(x ) = ( x+2)/( x-2)`
prove that f(x) f(-x) +f(0) =0
View Solutionfind the domain and range of the real function `f(x) = sqrt(9 -x^2)`
View SolutionR is the set of real number . Define the function `f :R to R ` by `f (x ) =x^2 + 3 `
find f(-1) and f(2)
View SolutionR is the set of real number . Define the function `f: R to R ` by ` f (x ) =x^2 + 3 `
Draw the graph of f(x)
View SolutionDraw the graph of the function f :R `to` R defined by
` f(x) =x^3 , x in R `
find its domain and range
View SolutionThe function f is defined by
` f(x) = {{:(1-x, x lt 0) ,( 1, x=0),( x+1,x gt 0):}`
draw the graph of f(x) .
View SolutionDraw the graph of the function ` f(x ) = {{:(1+x , -1 le x le 0),( 1-x, 0 lt x le 1):}`
View SolutionFind the range of the function
` f(x) = [ 2 x ] , 1/3 le x le (8)/(3)`
View Solution`f(x) = x^2 +1 ,0 le x le 2 `
find the range of the function f.
View Solution`f(x) = x^2 +1 ,0 le x le 2 `
find the range of the function f.
View Solution`f(x) = x^2 +1 ,0 le x le 2 `
find the range of the function f.
View SolutionWrite the equations for the x-and y-axes.
View Solutionconsider the functions
` f(x) = sqrt(x-2) , g(x) = ( x+1)/( x^2 -2x +1)`
domain of f
View Solutionconsider the functions
` f(x) = sqrt(x-2) , g(x) = ( x+1)/( x^2 -2x +1)`
domain of g
View Solutionconsider the functions
` f(x) = sqrt(x-2) , g(x) = ( x+1)/( x^2 -2x +1)`
`(fg)(x)`
View Solutionconsider the functions
` f(x) = sqrt(x-2) , g(x) = ( x+1)/( x^2 -2x +1)`
`(fg)(x)`
View SolutionLet R be the set of reals . Define a function `F : R to R ` by f (x) `= 2x^2-1`
find ` ( f(-1)+f(1))/( 2) `
View SolutionLet R be the set of reals . Define a function `F : R to R ` by f (x) `= 2x^2-1`
find f(f(x))
View SolutionLet R be the set of reals . Define a function `F : R to R ` by f (x) `= 2x^2-1`
draw the graph of f (x).
View Solutionfind the domain and range of the following real functions
`f(x ) =-|X|`
View SolutionThe function 't' which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by `t(C)=(9C)/(5)+32`
Find (i) t(0) (ii) t(28) (iii) t(-10) (iv) The value of C, when t(C)=212.
View SolutionThe function 't' which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by `t(C)=(9C)/(5)+32`
Find (i) t(0) (ii) t(28) (iii) t(-10) (iv) The value of C, when t(C)=212.
View SolutionThe function 't' which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by `t(C)=(9C)/(5)+32`
Find (i) t(0) (ii) t(28) (iii) t(-10) (iv) The value of C, when t(C)=212.
View SolutionFind the range of each of the following functions
f(x) =2-3x , ` x in R , x gt 0`
View SolutionFind the range of each of the following functions
` f(x ) = x^2+2 ,` x is real number
View SolutionFind the range of each of the following functions
f (x) = x,x is real number
View SolutionThe relation f is defined by `f(x)={{:(,x^(2), 0 le x le 3),(,3x,3 le x le 10):}`
The relation g is defined by `g(x)={{:(,x^(2),0 le x le 2),(,3x,2 le x le 10):}`
Show that f is a function and g is not a function.
View SolutionIf ` f(x) = x^2 ` find ` ( f (1.1 ) - f(1) )/( (1.1-1))`
View Solutionfind the domain of the function ` f(x) = (x^2 +2x + 1)/( x^2 -8x + 12 ) `
View Solutionfind the domain and the range of the real functions f defined by ` f(x) = |x-1|`
View SolutionLet `{(x ,(x^2)/(1+x^2)):x in R}` be a function from R into R Determine the range of f .
View SolutionLet f,g :` R to R ` defined , respectively by` f(x) = x+1 , g(x) = 2x -3 `, find f+ g,f-g and` (f)/( g) `
View SolutionLet f be a subset of ` Z xx Z ` defined by f ={ (ab ,a+b) : a,b in Z }` is f a function from z to Z ? Jusity your answer
View SolutionLet R be relation from N into N defined by R `={(a,b) : a,b in N ,a=b^2 }` are the following true ? Justify your answer in each case .
`(a,a) in R ` for all ` a in N`
View SolutionLet R be relation from N into N defined by R `={(a,b) : a,b in N ,a=b^2 }` are the following true ? Justify your answer in each case for all a,b. (a,b) `in R` implies (b,a) ` in R `
View SolutionLet R be relation from N into N defined by R `={(a,b) : a,b in N ,a=b^2 }` are the following true ? Justify your answer in each case .
`(a,b) and (b,c) in R ` for all `a,b,c, in N` implies (a,c) `in ` R
View SolutionLet `A = {1,2,3,4),B={1,5,9,11,15,16} and f= {(1,5),(2,9),(3,1) ,(4,5) ,(2,11)}`
are the following true
f is a relation from A to B
View SolutionLet `A = {1,2,3,4),B={1,5,9,11,15,16} and f= {(1,5),(2,9),(3,1) ,(4,5) ,2,11)}`
are the following true
f is a function from A to B
View Solution
EXAMPLES questions and complete solutions for chapter RELATIONS AND FUNCTIONS of NEW JYOTHI MATHS (TAMIL ENGLISH) of Class 12