Complete Solutions to MCQs LEVEL - II of chapter CIRCLES AND SYSTEMS OF CIRCLES of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | CIRCLES AND SYSTEMS OF CIRCLES |
| MODERN PUBLICATION | MCQs LEVEL - II |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
The equation of the circle in the first quadrant touching each co-ordinate axis at a distance of one unit from the origin is:
View SolutionThe equation of the circle having centre (1, 2) and passing through the point of intersection of the lines: 3x+y=14 and 2x+5y=18 is :
View SolutionThe area of the circle centred at (1, 2) and passing through (4,6) is :
View SolutionEquation of a circle which passes through (3, 6) and touches the axes is:
View SolutionEquation of the circle with centre on the y-axis and pussing through the origin und the point (2, 3) is :
View SolutionThe equation of a circle with origin as centre and passing through the vertices of an equilateral triangle whose median is of length 3a is:
View SolutionThe tangent to the circle `x^2 + y^2` = 9, which is parallel to y-axis and does not lie in the third quadrant, touches the circle at the point:
View SolutionThe angle between the tangents from the origin to the circle `(x-7)^2 +(y+1)^2=25` is :
View SolutionThe circle on the chord x cos `alpha` + y sin `alpha`-p= 0 of the circle `x^2 + y^2 - 2 = 0` as diameter is:
View SolutionThe equation to the circle which intersects the circles: `x^2+y^2-6y+1=0` and `x^2+y^2-4y+1=0` orthogonally and touch the line 3x+4y+5=0 is given by :
View SolutionThe number of integral values of k for which : `x^2+y^2 +kx +(1-k)y+5=0` represents a circle whose radius cannot exceed 5, is:
View SolutionIf the centroid of an equilateral triangle is (1, 1) and its one vertex is (-1, 2), then the equation of the circumcentre is :
View SolutionA foot of the normal from the point (4, 3) to a circle is (2, 1) and a diameter of the circle has the equation 2x - y = 2. Then the circle is:
View SolutionA tangent to the circle `x^2 + y^2 = 1` through the point (0, 5) cuts the centre `x^2 + y^2 = 4` at P and Q. The tangents to the circle `x^2 + y^2 = 4` at P and Q meet at R. Then the co-ordinates of R are :
View SolutionThe abscissae of two points P and Q are the roots of the equation `x^2 + 2ax – b^2 = 0` and their ordinates are the roots of the equation `x^2 + 2a'x-b^2 = 0`. Then the radius of the circle having PQ as diameter is :
View SolutionIf the polar of a point P w.r.t. the circle `x^2+y^2=a^2` touches the circle `(x- a)^2 + y^2 = a^2`, then P lies on:
View SolutionThe locus of the poles of the line ax + by + c = 0 w.r.t. circles which touch the x-axis at the origin is:
View SolutionLength of tangent drawn from any point on the circle `x^2+y^2+2gx + 2fy +c=0` to the circle :
`x^2+y^2+2gx+2fy+c'=0` is :
View SolutionThe tangents drawn from the origin to the circle : `x^2+y^2-2gx-2fy+f^2=0` are perpendicular if:
View SolutionIf a circle of constant radius 3k passes through the origin and meets the axes in A and B, then the locus of the centroid of `triangleOAB` is :
View SolutionIf the chord of contact of tangents from a point P `(x_1,y_1)` to the circle `x^2+y^2=a^2` touches the circle `(x-a)^2+y^2 = a^2`, then the locus of `(x_1, y_1)` is :
View SolutionThe equation of a circle which has a tangent 3x + 4y = 6 and two normals given by (x - 1)(y-2) = 0 is :
View SolutionThe tangent to `x^2 + y^2= 9`, which is parallel to y-axis and does not lie in the third quadrant, touches the circle at the point :
View SolutionThe circle `x^2 + y^2 - 6x - 10y + k = 0` does not touch or intersect the x-axis and the point (1, 4) lies inside the circle, then:
View SolutionTwo tangents to the circle `x^2 + y^2 = 4` at the points A and B meet at P (- 4, 0). Then the area of the quadrilateral PAOB, O being the origin, is :
View SolutionIf the radical axis of the circles `x^2+y^2+2gx+2fy+c=0` and `2x^2+2y^2+3x+8y+2c=0` touches the circle :
`x^2+y^2+2x+2y+1=0` , then :
View SolutionThe equation of the circle having its centre on the line x +2y - 3 = 0 and passing through the points of intersection of the circles `x^2 + y^2 - 2x - 4y +1 = 0` and `x^2+y^2 -4x -2y +4=0` is :
View SolutionThe number of common tangents to the circles `x^(2) + y^(2) = 4` and `x^(2) +y^(2) - 6x - 8y -24 =0` is,
View SolutionNumber of common tangents to the circles : `x^2+y^2 -6x-14y+48=0` and `x^2+y^2-6x=0` is :
View SolutionThe locus of the centre of a circle which cuts orthogonally the circle `x^2+y^2 -20x+4=0` and which touches x = 2 is :
View SolutionCo-ordinates of radical centre of the circles : `x^2+y^2 = 9 , x^2+y^2 -2x -2y =5` and `x^2+y^2 +4x + 6y =19` are :
View SolutionThe equation of the family of circles, which same radical axis, as the circles :
`x^2+y^2`=4 and `x^2+y^2+2x+4y=6` is :
View SolutionIf one of the circles: `x^2+y^2 +2ax+c=0` and `x^2+y^2 + 2bx+c=0` lies within the other , then :
View SolutionThe radius of the smallest circle, which passes through the points of intersection of the circles : `x^2+y^2+2x-3=0` and `x^2+y^2 +3x-y=0` is :
View SolutionThe equation of the four circles are `(x pm a)^2 + (y pm a)^2 = a^2`. The radius of the smallest circle, which touches all the four circles, is:
View SolutionThe circles : `x^2+y^2 +2g_1x-a^2 =0` and `x^2+y^2 +2g_2x-a^2=0` cut each other orthogonally. Let `p_1` and `p_2` be the perpendiculars from (0, a) and (0, - a) on the common tangent of these circles. Then `p_1p_2` equals :
View SolutionIf the circle `x^2+y^2+2gx+2fy+c=0` bisects the circumference of the circle `x^2+y^2+2g'x +2f'y+c'=0` , then :
View SolutionLet AB be a chord of the circle `x^2+y^2=a^2` subtending a right angle at the centre. Then the locus of the centroid of triangle PAB as P moves on the circle is:
View SolutionLocus of centroid of the triangle whose vertices are (a cos t, a sin t),(b sin t , - b cos 1) and (1, 0), where 't' is a parameter, is :
View SolutionIf the circles `x^2 + y^2 + 2ax + cy+ a = 0` and `x^2 + y^2 - 3ax + dy - 1 = 0` intersect in two distinct points P and Q, then the line 5x + by - a = 0 passes through P and Q for :
View SolutionIf a circle passes through the point (a, b) and cuts the circle `x^2+y^2=p^2` orthogonally, then the equation of the locus of its centre is:
View SolutionIf the pair of lines `ax^2 +2 (a + b) xy + by^2 =0` lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sectors, then:
View SolutionIf the lines 3x - 4y - 7 = 0 and 2x - 3y - 5 = 0 are two diameters of a circle of area 49`pi` square units, then the equation of the circle is:
View SolutionLet 'C' be the circle with centre (0,0 ) and radius 3 units. The equation of the locus of the mid points of chords of the circle 'C' that subtend an angle of `2pi//3` at its centre is:
View SolutionLet ABCD be a quadrilateral with area 18, with side AB parallel to the side CD and AB = 2 CD. Let AD be perpendicular to AB and CD. If a circle is drawn inside the quadrilateral ABCD touching all the sides, then its radius is :
View SolutionConsider a family of circles which are passing through the point (-1, 1) and are tangent to x-axis. If (h,k) are the co-ordinates of the centre of the circle, then the set of values of k is given by the interval :
View SolutionThe point diametrically opposite to the point P (1, 0) on the circle `x^2+y^2+2x+4y-3=0` is :
View SolutionIf P and Q are the points of intersection of the circles `x^2+y^2+3x+7y+2p-5=0` and `x^2+y^2+2x+2y-p^2=0`, then there is a circle passing through P, Q and (1, 1) for :
View SolutionIf a variable circle 'C' touches the x-axis and touches the circle `x^2+(y-1)^2=1` externally, then the locus of centre of 'C' can be:
View SolutionThree coins of unit radius are placed in an equilateral triangle as shown in the following figure. The area of that equilateral triangle is :
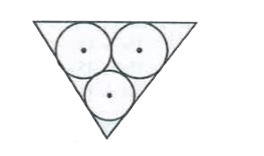
View SolutionTangents drawn from the point P (1, 8) to the circle `x^2+ y^2 - 6x - 4y - 11 = 0` touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View Solution
MCQs LEVEL - II questions and complete solutions for chapter CIRCLES AND SYSTEMS OF CIRCLES of MODERN PUBLICATION MATHS (KANNADA ENGLISH) of Class 12