Complete Solutions to प्रश्नावली of chapter दोलन of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | दोलन |
| ARIHANT HINDI | प्रश्नावली |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
x - अक्ष के अनुदिश गति करते हुए 0.1 किग्रा द्रव्यमान की स्थितिज ऊर्जा `U=5x(x-4)` जहाँ x मीटर में है , द्वारा दी जाती है , तो असत्य विकल्प है
View Solutionमध्यमान स्थिति 3 सेमी दुरी पर सरल आवर्त गति करते हुये एक कण का त्वरण `12"सेमी/से"^(2)` है। इसका आवर्तकाल है
View Solutionसरल आवर्त गति करते हुये एक कण का आवर्तकाल T सेकंड एवं आयाम a मीटर है। माध्य स्थिति से `(a)/(sqrt(2))` मीटर की दुरी पर स्थित बिंदु तक पहुंचने में इसके द्वारा लिया गया न्यूनतम समय है ?
View Solutionदो सरल आवर्त गतियाँ , समीकरण `x=asin(omegat-a)` तथा `y=b cos(omegat-a)` द्वारा प्रदर्शित की जा रही हैं। इनके बीच कलांतर होगा
View Solutionएक सिक्का किसी क्षैतिज प्लेटफॉर्म में रखा जो अपनी माध्य स्थिति O के इर्द - गिर्द क्षैतिज सरल आवर्त गति करता है। यदि सरल आवर्त गति की कोणीय आवर्ती `omega` हैं ,तो सिक्का प्लेटफॉर्म पर फिसलता नहीं है। सिक्के व् प्लेटफॉर्म के मध्य घर्षण गुणांक `mu` है। दोलन के आयाम उत्तरोतर बढ़ते जाते हैं। पहेली बार सिक्का फिसलने की स्थितिज में होगा
View Solutionएक ब्लॉक किसी क्षैतिज टेबल पर विरामावस्था में हैं। टेबल क्षैतिज ताल में a आयाम से सरल आवर्त दोलन करती है। घर्षण गुणांक `mu` है तो वह आवर्ती जिस पर ब्लॉक फिसलने की अवस्था में होगा
View Solutionसमान बल नियतांक k वाली तीन स्प्रिंगों A , B और C से m द्रव्यमान का एक कण चित्र में दिखाये अनुसार जुड़ा है। यदि कण को स्प्रिंग A के विरुद्ध हल्का सा दबा कर छोड़ा जाये तो दोलनकाल होगा

View Solutionएक वस्तु सरल आवर्त गति कर रही है। इसकी गतिज ऊर्जा KE और समय t के मध्य सही ग्राफ होगा
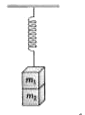
View Solution`m_1` और `m_2` दो द्रव्यमान K नियतांक वाली किसी द्रव्यमान विहीन स्प्रिंग से चित्र में दिखाए अनुसार लटके है। संतुलन की अवस्था में, निकाय को प्रभावित न करके यदि `m_1` को धीरे से हटा लिया जाए तो दोलन का आयाम होगा।
View Solutionएक कण 4 सेमी आयाम की सरल आवर्त गति कर रहा है। साम्यावस्था से कितने विस्थापन पर इसकी ऊर्जा आधी स्थितिज व् आधी गतिज होगी ?
View Solutionएक कण अपनी साम्यावस्था की स्थिति से T आवर्तकाल के दोलन प्रारम्भ करता है। `t=(T)/(12)` पर गतिज ऊर्जा व स्थितिज ऊर्जा का अनुपात होगा
View Solutionसमुन्द्र तल के सापेक्ष पर्वत पर g का मान `0.1%` कम हो जाता है। इस जगह पर सही समय ज्ञात करने के लिए सरल लोलक की लम्बाई में करनी चाहिए
View Solutionदो कण A व B क्रमशः T व `(5T)/(4)` आवर्तकालों वाली सरल आवर्त गति कर रहें हैं। दोनों साम्यावस्था से प्रारम्भ करते हैं , जिस समय कण A एक दोलन पूरा कर लेता है , उस समय उनके बीच कलांतर होगा
View Solutionएक कण x - अक्ष के अनुदिश सरल आवर्त गति कर रहा है जिसका आयाम 4 सेमी तथा आवर्तकाल 1.2 सेकंड है, तो कण द्वारा `x=+2` सेमी से `x=+4` सेमी तक जाने तथा वापस आने में लिया गया न्यून्तम समय है
View Solutionएक पीतल का घन जिसकी प्रत्येक भुजा की लम्बाई A तथा घनत्व `sigma` है , `rho` घनत्व वाले पारे में तैर रहा है। यदि घन को थोड़ा - सा ऊर्ध्वाधरतः दबाकर छोड़ दिया जाये , तो यह सरल आवर्त गति करने लगता है। इसका दोलनकाल होगा
View Solutionएक स्थिर लिफ्ट में सरल लोलक का आवर्तकाल T है। यदि लिफ्ट 5 g त्वरण से ऊपर की ओर गति करने लगे , तो इसका आवर्तकाल
View Solutionएक सरल लोलक ट्रॉली की छत से लटका हुआ है। ट्रॉली क्षैतिज सीधा में A त्वरण से गति कर रही है। सरल लोलक का आवर्तकाल `T=2pisqrt((l)/(g'))` में g ' होगा
View Solution4 न्यूटन बल आरोपित करने पर किसी स्प्रिंग की लम्बाई `alpha` है। 5 न्यूटन बल आरोपित करने पर लम्बाई `beta` है। 9 न्यूटन का बल आरोपित करने पर स्प्रिंग की लम्बाई होगी
View Solutionएक सरल लोलक के दोलन का द्रव्यमान m व् आवेश q है। आलम्बन बिंदु एक `sigma` सतह आवेश घनत्व के क्षैतिज तल पर स्थित है। साम्यावस्था में लोलक का धागा ऊर्ध्वाधर से `theta` कोण बनाता है। यदि आवर्तकाल T हो , तो
View Solutionएक सरल लोलक की लम्बाई l है और इसका अधिकतम कोणीय विस्थापन `theta` है , इसकी अधिकतम गतिज ऊर्जा होगी
View Solutionकमानी स्थिरांक k की किसी कमानी से जुड़े m द्रव्यमान के कण की प्राकतिक कोणीय आवृति `omega_(0)` है। इस दोलित्र पर कोई बाह्य बल `F(t)`, जो `cos omega t(omeg ne omega_(0))` के अनुक्रमानुपाती किया जाता है। इस दोलित्र का समय विस्थापन अनुक्रमानुपाती किया जाता है। इस दोलित्र का समय विस्थापन अनुक्रमानुपाती होगा
View Solutionद्रव्यमान m का एक छोटा गोला , l लम्बाई के धागे से सरल लोलक के रूप में लटका है। गोले पर धनात्मक आवेश q है। लोलक ऊपर की और निर्देशित एकसमान विधुत क्षेत्र में रखा है। यदि विधुत स्थैतिक बल गुरुत्वाकर्षण बल से क्षीण में रखा है , तो लोलक किस आवर्तकाल से दोलन करेगा ?

View Solutionएक बेलनाकार पिस्टन जिसका द्रव्यमान M है एक खोखले बेलन जिसका एक सिर बंद है, के भीतर गति कर सकता है। खोखले बेलन में गैस भरी हुई । यदि पिस्टन को संतुलन बिंदु से थोड़ा हटाकर छोड़ देने पर वह सरल आवर्त गति करने लगता है , तो इसका दोलनकार होगा

View Solutionएक सरल लोलक का कोणीय आयाम `theta_(0)` है। धागे में अधिकतम तनाव होगा
View Solutionएक द्रव का घनत्व गहराई के साथ इस प्रकार परिवर्तित होता है `rho=alphah`, द्रव की मुक्त सतह से `rho_(0)` घनत्व की एक गेंद को द्रव में छोड़ा जाता है , तो
View Solutionवक्तव्य I सरल आवर्त गति में त्वरण न्यूनतम होने की दशा में वेग अधिकतम होगा।
वक्तव्य II सरल आवर्त गति में विस्थापन और वेग की कला एक दूसरे से `(pi)/(2)` से अलग होती है।
View Solutionवक्तव्य I दोलन करते हुये सरल लोलक के दोलनों का आयाम धीरे - धीरे समय के साथ घटता है।
वक्तव्य II समय के साथ पेण्डुलम की आवृत्ति घटती है।
View Solutionवक्तव्य I दोलनों का आयाम कभी भी अनन्त नहीं हो सकता।
वक्तव्य II किसी दोलित्र की ऊर्जा में लगातार हानि होती है।
View Solutionवक्तव्य I अनुनाद प्रणोदित दोलन की एक विशेष अवस्था है , जिसमें दोलन की वास्तविक आवृत्ति बाह्य आवर्ती बल के आरोपित आवृत्ति के तुल्य होती है एवं प्रणोदित दोलन का आयाम अधिकतम होता है।
वक्तव्य II किसी वस्तु के प्रणोदित दोलनों का आयाम बाह्य आवृत्ति बल के आरोपित आवृत्ति बढ़ने के साथ बढ़ता है।
View Solutionएक प्लेटफॉर्म ऊर्ध्वाधर दिशा में 5 सेमी आयाम व् `(10)/(pi)` आर्स्टेड / से दर से सरल आवर्त गति कर रहा है। गति के निम्नतम बिंदु पर प्लेटफॉर्म पर एक ब्लॉक रख दिया जाता है। (दिया है `g=10"मी /से"^(2))`
किस स्थिति में ब्लॉक का प्लेटफॉर्म से सम्पर्क टूट जायेगा ?
View Solutionएक प्लेटफॉर्म ऊर्ध्वाधर दिशा में 5 सेमी आयाम व् `(10)/(pi)` आर्स्टेड / से दर से सरल आवर्त गति कर रहा है। गति के निम्नतम बिंदु पर प्लेटफॉर्म पर एक ब्लॉक रख दिया जाता है। (दिया है `g=10` मी /से `""^(2))`
सही कथन को चिन्हित कीजिये
View Solutionएक प्लेटफॉर्म ऊर्ध्वाधर दिशा में 5 सेमी आयाम व् `(10)/(pi)` आर्स्टेड / से दर से सरल आवर्त गति कर रहा है। गति के निम्नतम बिंदु पर प्लेटफॉर्म पर एक ब्लॉक रख दिया जाता है। (दिया है `g=10"मी /से"^(2))`
किस स्थिति में ब्लॉक का प्लेटफॉर्म से सम्पर्क टूट जायेगा ?
View Solutionएक कण सरल रेखा में सरल आवर्त गति करता है। A व् B दो बिंदु है जहाँ कण का वेग शून्य हैं। कण किसी बिंदु X से `(AXltBX)1.2` सेकंड व् 3.6 सेकंड के उत्तरोत्तर समयान्तराल पर `4` मी/से की चाल से गुज़रता है।
दोलन के आयाम हैं
View Solutionएक कण सरल रेखा में सरल आवर्त गति करता है। A व् B दो बिंदु है जहाँ कण का वेग शून्य हैं। कण किसी बिंदु X से `(AXltBX)1.2` सेकंड व् 3.6 सेकंड के उत्तरोत्तर समयान्तराल पर `4 "मी/से"` की चाल से गुज़रता है।
कण का अधिकतम वेग होगा
View Solutionएक कण सरल रेखा में सरल आवर्त गति करता है। A व् B दो बिंदु है जहाँ कण का वेग शून्य हैं। कण किसी बिंदु X से `(AXltBX)1.2` सेकंड व् 3.6 सेकंड के उत्तरोत्तर समयान्तराल पर `4` मी/से की चाल से गुज़रता है।
अनुपात `(AX)/(BX)` का मान है
View Solutionफलन `x=Asin^(2)omegat+Bcos^(2)omegat+Csinomegatcosomegat` सरल आवर्त गति नहीं प्रदर्शित करता है।
View Solutionसरल आवर्त गति करते हुये किसी कण का विस्थापन समीकरण `y=4cos^(2)((t)/(2))sin(1000t)` द्वारा प्रदर्शित होता है। यह व्यंजक कितनी स्वतंत्र आवर्त गतियों के आध्यारोपणो का परिणाम कहा जा सकता है ?
View Solution
प्रश्नावली questions and complete solutions for chapter दोलन of ARIHANT PHYSICS (HINDI) of Class 12