Complete Solutions to EXERCISE - 01 (सही विकल्प चुनिए (केवल एक सही उत्तर है ) of chapter METHODS OF DIFFERENTIATION of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | METHODS OF DIFFERENTIATION |
| ALLEN HINDI | EXERCISE - 01 (सही विकल्प चुनिए (केवल एक सही उत्तर है ) |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
यदि `y=(secx-tanx)/(sec x + tanx)` तो `(dy)/(dx)` बराबर है
View Solutionयदि `y=(1+x^2+x^4)/(1+x+x^2)` तथा `(dy)/(dx) = ax+b` हो , तो a तथा b के मान होंगे -
View Solutionनिम्न में से `y=(d)/(dx) (xlnx)` का आरेख हो सकता है -
View Solutionमाना `f(x) = x + 3 ln(x-2) ` तथा `g(x) = x + 5 ln (x-1)` , तब असमिका `f'(x) lt g'(x)` को संतुष्ट करने वाले का मानों का समुच्चय है -
View Solutionx के सापेक्ष `(x^((l+m)/(m-n)))^(1/(n-l)).(x^((m+n)/(n-l)))^(1/(l-m)).(x^((n+l)/(l-m)))^(1/(m-n))` का अवकलन गुणांक है
View Solutionयदि `y=1/(1+x^(n-m)+x^(p-m))+1/(1+x^(m-n)+x^(p-n))+1/(x^(m-p)+x^(n-p))` हो, तो `e^(mnp)` पर `(dy)/(dx)` बराबर है -
View Solutionयदि `cos^(-1)""((x^2-y^2)/(x^2+y^2))=loga` तो `(dy)/(dx) = 0 `
View Solutionयदि `f(x)=Pi_(n=1)^(100)(x-n)^(n(101-n))` तो `f(101)/(f'(101))=`
View Solutionयदि `f(x) = (|x|)^(|sinx|)` , तो `f'(-pi/4)` का मान है -
View Solutionयदि `y=(x)/(a+) (x)/(b+) (x)/(a+)x/(b+)x/(a+)x/(b+)........oo` तो `(dy)/(dx)=`
View Solutionयदि `y = x^(x^2)` तो `(dy)/(dx)= `
View Solutionयदि `x^(m).y^(n)=(x+y)^(m+n)` तो `(dy)/(dx)` है -
View Solutionयदि `xsqrt((1+y))+ysqrt((1+x))=0` तो `(dy)/(dx)` बराबर है -
View Solutionयदि `x^(2)e^(y)+2xye^(x)+13=0` तो `(dy)/(dx)` बराबर है -
View Solutionयदि `x=e^(y+e^(y+....."to"oo)),xgt0` तो `(dy)/(dx)` है -
View Solutionयदि `x = theta - 1/(theta)` तथा ` y = theta +1/(theta)` , तो `(dy)/(dx)` बराबर है -
View Solution`sin^(-1)""(x/(sqrt(1+x^2)))` का `cos^(-1)""((1-x^2)/(1+x^2)), (x gt0)` के सापेक्ष अवकलज होगा -
View Solutionमाना f का प्रतिलोम फलन g तथा f'(x) `= (x^(10))/((1+x^2))` है , यदि `g (2) = a` हो ,तो g'(2) बराबर है -
View Solutionमाना f(x) = sinx, g(x) `=x^2` तथा `h(x) = log_(e)x` एवं `F(x) = h [g(f(x))]` हो , तो `(d^2F)/(dx^2)` बराबर है -
View Solutionयदि `f(x)=sqrt(x^2+1),g(x)=(x+1)/(x^2+1)` तथा `h(x) = 2x - 3 `, तो ` f'(h'(g'(x))` =
View Solutionयदि f तथा g फलन है, जिनके आरेख दर्शाए गए हैं, माना `u(x) = f (g(x)), w(x) = g(g(x))` हो, तो u'(1) +w'(1) का मान होगा
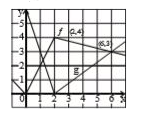
View Solution`f'(x) =g(x)` तथा `g'(x) =-f(x), AAx` तथा f(5) = 2 = f'(5) तब `f^(2)(10)+g^2(10)` का मान है -
View Solutionयदि `f(x) = x^(n)` तो `f(1)-(f'(1))/(1!)+(f''(1))/(2!)-(f'''(1))/(3!)+......+((-1)^(n)f^('''''''''....("n times"))(1))/(n!)` का मान होगा
View Solutionफलन `y=f(x)` का द्वितीय क्रम का अवकलज `f ''(x) = 6(x-1)` है। यदि इसका आरेख बिन्दु `(2,1)` से गुजरता हो तथा ग्राफ से इस बिन्दु पर स्पर्श रेखा `y =3x-5` हो, तब फलन, होगा-
View Solutionयदि `f(x)=x+(x^2)/(1!)+x^3/(2!)....(x^n)/((n-1)!)` है, तो `f (0) + f'(0) + f''(0) + ...... + f^(''''....n)` ..... बार (0) बराबर होगा -
View Solutionमाना `f(x)=|(cosx,x,1),(2sinx,x^2,2x),(tanx,x,1)|` हो , तो `{:("Limit"),(x rarr0):}(f'(x))/(x)=`
View Solutionयदि (0,6) पर f अवकलनीय है तथा f'(4) =5 हो, तो `Lim_(xrarr2)(f(4)-f(x^2))/(2-x)=`
View Solutionयदि `f(4) = g(4) = 2` `f'(4) = 9`, `g'(4) = 6` हो, तो `{:("Limit"),(x rarr4):} (sqrt(f(x))-sqrt(g(x)))/(sqrtx-2)` बराबर है -
View Solution
EXERCISE - 01 (सही विकल्प चुनिए (केवल एक सही उत्तर है ) questions and complete solutions for chapter METHODS OF DIFFERENTIATION of ALLEN HINDI of Class 12
All Exercises from ALLEN HINDI Class 12 MATHS METHODS OF DIFFERENTIATION
- Do yourself
- EXERCISE - 01 (सही विकल्प चुनिए (केवल एक सही उत्तर है )
- EXERCISE - 01 (सही विकल्पों को चुनिए (एक या एक से अधिक सही उत्तर है)
- EXERCISE - 02 (सही विकल्पों को चुनिए (एक या एक से अधिक सही उत्तर हैं)
- EXERCISE - 03 (MISCELLANEOUS TYPE QUESTIONS ) (सत्य / असत्य)
- EXERCISE - 03 (MISCELLANEOUS TYPE QUESTIONS ) (स्तम्भ सुमेलन)
- EXERCISE - 03 (MISCELLANEOUS TYPE QUESTIONS )(कथन एवं कारण )
- EXERCISE - 04 [A]
- EXERCISE - 04 [B]
- EXERCISE - 05 [A]
- EXERCISE - 05 [B]
- उदाहरण