Complete Solutions to Exercise-3 of chapter DIFFERENTIABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | DIFFERENTIABILITY |
| ALLEN HINDI | Exercise-3 |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
`[tan^(2)x], x=0` पर संतत तथा अवकलनीय है । (जबकि [.] महत्तम पूर्णांक को निरूपित करता है)
View Solution`e^(-|x|), x = 0` पर अवकलनीय है।
View Solutionयदि f(x) हर जगह अवकलनीय है, तब `|f(x)|^(2)` हर जगह अवकलनीय है।
View Solutionयदि किसी फलन की x=a पर स्पर्श रेखा है तब वक्र x=a पर अवकलनीय होगा।
View Solutionयदि f(x) तथा g(x) दोनों किसी बिंदु पर असंतत है, तब उस बिंदु पर उनका संयुक्त फलन अवकलनीय हो सकता है
View Solution
View Solution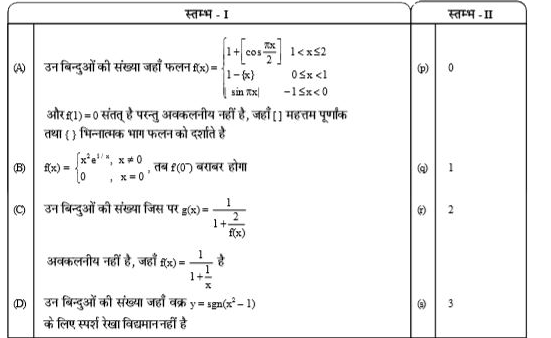
View Solutionमाना `f(x)= ax^(2) + bx + c, a, b, c in R` तथा `a ne 0` है।
कथन-I : यदि f(x) =0 के दो भिन्न धनात्मक वास्तविक हल है ऋ तो बिन्दुओ की संख्या जहाँ `y= |f(-|x|)|` अवकलनीय नहीं होगा, 1 होगी।
क्योकि
कथन -II `y= f (|x|)` का आरेख y-अक्ष के सापेक्ष सम्मित होगा।
View Solutionकथन-I `|x^(3)|, x = 0` पर अवकलनीय है।
क्योकि
कथन-II यदि f(x) x= a पर अवकलनीय है, तो |f(x)| भी x=a पर अवकलनीय है।
View Solutionकथन-I : `f(x) = |x|.sin x, x= 0` पर अवकलनीय है।
क्योकि
कथन-II यदि f(x) x= a पर अवकलनीय नहीं है तथा g(x), x=a अवकलनीय है, तो f(x).g(x), x= a पर अवकलनीय होगा।
View Solutionमाना `f(x)= cos (sin^(-1)x)`, जो कि `(-1, 1)` में अवकलनीय है।
कथन-I : `f(x), [-1, 1]` में परिबद्ध फलन है।
क्योकि
कथन-II : यदि एक फलन (a,b) में अवकलनीय हो, तो वह [a,b] में परिबद्ध होगा।
View Solution`f(x)= {(2+(x-1)^(2),"यदि ",x lt 1),(2,"यदि ",x in [1"," 3]),(2-(x-3)^(2),"यदि ",x gt 3):}`
`g(x)= {:(2+ sqrt-x,"यदि ",xlt 0),(x+2,"यदि ",x in [0, 4]),(3x-6,"यदि ",x in (4 ","oo)):}`
`h(x)= {(4+ ae^(x),"यदि ",x lt0),(x+2,"यदि ",x in [0, 3]),(b^(2)-7b+ 18- (3)/(x),"यदि ",x gt 3):}`
`k(x)= sqrt(1+x sqrt(1 + (x+1) sqrt1 + (x+2) (x+4))), x gt 0`
उपरोक्त जानकारी के आधार पर, निम्न प्रश्नो के उत्तर दीजिये-
निम्न में से कौन अपने प्रान्त के प्रत्येक बिंदु पर संतत है -
View Solution`f(x)= {(2+(x-1)^(2),"यदि ",x lt 1),(2,"यदि ",x in [1"," 3]),(2-(x-3)^(2),"यदि ",x gt 3):}`
`g(x)= {:(2+ sqrt-x,"यदि ",xlt 0),(x+2,"यदि ",x in [0, 4]),(3x-6,"यदि ",x in (4 ","oo)):}`
`h(x)= {(4+ ae^(x),"यदि ",x lt0),(x+2,"यदि ",x in [0, 3]),(b^(2)-7b+ 18- (3)/(x),"यदि ",x gt 3):}`
`k(x)= sqrt(1+x sqrt(1 + (x+1) sqrt1 + (x+2) (x+4))), x gt 0`
उपरोक्त जानकारी के आधार पर, निम्न प्रश्नो के उत्तर दीजिये-
(a,b) का मान जिसके लिए h(x), सभी `x in R` के लिए संतत है, होगा
View Solution`f(x)= {(2+(x-1)^(2),"यदि ",x lt 1),(2,"यदि ",x in [1"," 3]),(2-(x-3)^(2),"यदि ",x gt 3):}`
`g(x)= {:(2+ sqrt-x,"यदि ",xlt 0),(x+2,"यदि ",x in [0, 4]),(3x-6,"यदि ",x in (4 ","oo)):}`
`h(x)= {(4+ ae^(x),"यदि ",x lt0),(x+2,"यदि ",x in [0, 3]),(b^(2)-7b+ 18- (3)/(x),"यदि ",x gt 3):}`
`k(x)= sqrt(1+x sqrt(1 + (x+1) sqrt1 + (x+2) (x+4))), x gt 0`
उपरोक्त जानकारी के आधार पर, निम्न प्रश्नो के उत्तर दीजिये-
निम्न में से कौनसा फलन अपने प्रान्त के केवल दो बिन्दुओ पर अवकलनीय नहीं है-
View Solutionमाना f' एक फलन है जो कि हर जगह अवकलनीय है तथा उसके निम्न गुणधर्म है:
(i) `f(x) gt 0` (ii) `f'(0)= -1` (iii) `f(-x)= (1)/(f(x)) " &" f(x + h)= f(x).f(h)`
मानक परिणाम : `int (f'(x))/(f(x)) dx= ln |f(x)| + c`
उपरोक्त जानकारी के आधार पर, निम्न प्रश्नो के उत्तर दीजिये:
f(x) का परिसर है-
View Solutionमाना f' एक फलन है जो कि हर जगह अवकलनीय है तथा उसके निम्न गुणधर्म है:
(i) `f(x) gt 0` (ii) `f'(0)= -1` (iii) `f(-x)= (1)/(f(x)) " &" f(x + h)= f(x).f(h)`
मानक परिणाम : `int (f'(x))/(f(x)) dx= ln |f(x)| + c`
उपरोक्त जानकारी के आधार पर, निम्न प्रश्नो के उत्तर दीजिये:
फलन `Delta = f(|x|)` का परिसर है-
View Solutionमाना f' एक फलन है जो कि हर जगह अवकलनीय है तथा उसके निम्न गुणधर्म है:
(i) `f(x) gt 0` (ii) `f'(0)= -1` (iii) `f(-x)= (1)/(f(x)) " &" f(x + h)= f(x).f(h)`
मानक परिणाम : `int (f'(x))/(f(x)) dx= ln |f(x)| + c`
उपरोक्त जानकारी के आधार पर, निम्न प्रश्नो के उत्तर दीजिये:
फलन y= f(x) है-
View Solutionमाना f' एक फलन है जो कि हर जगह अवकलनीय है तथा उसके निम्न गुणधर्म है:
(i) `f(x) gt 0` (ii) `f'(0)= -1` (iii) `f(-x)= (1)/(f(x)) " &" f(x + h)= f(x).f(h)`
मानक परिणाम : `int (f'(x))/(f(x)) dx= ln |f(x)| + c`
उपरोक्त जानकारी के आधार पर, निम्न प्रश्नो के उत्तर दीजिये:
यदि h(x) = f'(x) तब h(x) निम्न से दिया जायेगा-
View Solution
Exercise-3 questions and complete solutions for chapter DIFFERENTIABILITY of ALLEN HINDI of Class 12