Complete Solutions to EXERCISE-04 [A] (CONCEPTUAL SUBJECTIVE EXERCISE) of chapter MAXIMA-MINIMA of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MAXIMA-MINIMA |
| ALLEN HINDI | EXERCISE-04 [A] (CONCEPTUAL SUBJECTIVE EXERCISE) |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
निम्न फलनों के स्थानीयउच्चिष्ठ/ निम्नष्ठ बिन्दु ज्ञात कीजिए :
(a) `f(x)=2x^(3)-21x^(3)+36x-20 " " (b) f(x)=-(x-1)^(3)(x+1)^(2)`
(c) `f(x)=x lnx " " (d) y={:(3x^(2)+4x+4),(x^(2)+x+1):}`
View Solutionमाना `f(x)={{:(-x^(3)+((b^(3)-b^(2)+b-1))/((b^(2)+3b+2))",",0 le x lt1),(2x-3",", 1 le x le3):}` है। b के सभी संभव वास्तविक मान ज्ञात कीजिए ताकि f(x) का न्यूनतम मान x=1 पर हो।
View Solutionएक घनीय बहुपद f(x), x =-2 पर लुप्त होता है तथा इसका सापक्षिक निम्निष्ठ/उच्चिष्ठ x =-1 तथा x = 1/3 पर है। यदि `overset(1) underset(-1) int f(x) dx=(14)/(3)` तो (f(x)) ज्ञात कीजिए |
View Solutionनिम्न फलनों के निर्पेक्ष उच्चिष्ठ निम्निष्ठ मान ज्ञात कीजिए :
(a) `f(x)=4x-(x^(2))/(2),x in [-2,(9)/(2)] " " (b) f(x)=3x^(4)-8x^(3)+12x^(2)-48x+25, x in [0,3]`
(c) `f(x)=sin x+(1)/(2) cos 2x, x in [0,(pi)/(2)]`
View Solutionमाना x तथा y दो वास्तविक चर इस प्रकार है कि `xgt 0` तथा `xy = 1` है। x + y का निम्निष्ठ मान ज्ञात कीजिए।
View Solutionएक आयतीय पृष्ठ का क्षेत्रफल 18m^(2) है। ऊपर व नीचे के हाशिये(margin) की चौड़ाई 75 सेमी तथा पार्श्व (let &right margin) की चौड़ाई 50 सेमी है। पृष्ठ की विमा क्या होने चाहिए ताकि छपे हुए भाग(printed space) का क्षेत्रफल महत्तम हो?
View Solutionयदि `y=(ax+b)/((x-1)(x-4))` का (2.-1) पर वर्तन बिन्दु (turnin g pt.) है, तब a तथा b ज्ञात कीजिए तथा दर्शाइये कि इस बिन्दु पर मान अधिकतम होगा।
View Solutionएक बाग त्रिज्यखण्ड के आकार में है, जिसकी त्रिज्या तथा केन्द्रीय कोण है। यदि क्षेत्रफल नियत तथा परिमाप न्यूनतम है, तब त्रिज्या तथा केन्द्रीय कोण ज्ञात कीजिए।
View Solutionअधिकतम क्षेत्रफल के आयत की विमा क्या होगी,जो कि त्रिभुज जिसका आधार 36 ft. तथा शीर्षलम्ब 12 11. है, में बनाया जा सकता है? यह माने कि आयत की एक भुजा, त्रिभुज के आधार पर स्थित है।
View Solutionप्रदर्शित कीजिये कि दिये गये कुल पृष्ठीय क्षेत्रफल एवं अधिकतम आयतन के लम्ब वृत्तीय शंकु का अर्द्ध शीर्ष कोण `sin^(-1) ""(1)/(3)` है।
View Solutionवक्र `y = ( 6)/( x^(2) + 3)` कि सभी स्पर्श रेखाओं के लिये अधिकतम एवं न्यूनतम प्रवणता वाली स्पर्श रेखाओं के समीकरण ज्ञात कीजिये।
View Solutionमाना कि फलन f(x), निम्न प्रतिबधों को संतुष्ट करता है
(i) `f(0)=2,f(1)=1`
यदि फलन f(x) का मान `x=(5)/(2)` पर न्यूनतम है।
(ii) x के सभी मानों के लिए `f'(x)=|{:(2ax,2ax-1,2ax+b+1),(b,b+1,-1),(2(ax+b),2ax+2b+1,(2ax+b)):}|`
जहाँ a, b अचर है। तो a, b तथा फलन f(x) ज्ञात कीजिए|
View Solutionमाना फलन `F(x)=overset(pi) underset(-1)int dt, x in R` है। ज्ञात कीजिए :
(a) Fx तथा y अन्तःखण्ड, यदि विद्यमान हो
(b) अवकलजF (x) तथा F"(x)
(c) वह अन्तराल जिस पर F वर्धमान तथा वह अन्तराल जहाँF ओसमान हो।
(d) सापेक्ष उच्चिष्ठ तथा निम्निष्ठ बिन्दु
(e) नति परिवर्तन बिन्दु
View Solutionअनुच्छेद : (प्र. 14 से 16)
यदि एक संतत् फलन `f` जो वास्तविक रेखा `R` पर परिभाषित है, `R` में धनात्मक तथा ऋणात्मक मान लेता है, तब समीकरण `f(x) = 0` का एक मूल R मे होगा। उदाहरण के लिए, यदि यह ज्ञात है की `R` के कुछ बिन्दुओं पर संतत् फलन `f` धनात्मक है तथा इसका न्यूनतम मान ऋणात्मक है, तब समीकरण `f(x) = 0` का एक मूल R में होगा।
माना `f(x) = ke^(x)` सभी वास्तविक `x` के लिए, जहाँ `k` एक वास्तविक अचर है।
`k gt 0` के लिए, k के सभी मानों का समुच्चय जिसके लिए `ke^(x) - x=0` के दो भिन्ना मूल होंगे, है-
View Solutionएक वृत्त `x^(2)+y^(2)=1` x-अक्ष को P तथा Q पर काटता है। दूसरा वृत्त जिसका केन्द्र Q पर है तथा चर त्रिज्या प्रथम वृत्त को x-अक्ष के ऊपर R पर तथा रेखा खण्ड PQ को S पर प्रतिच्छेद करती है। त्रिभुजQSR का अधिकतम क्षेत्रफल ज्ञात कीजिए।
View Solutionफलन `f(x) = int_(1)^(x) [2(t-1) ( t-2)^(3) + 3( t-1)^(2) ( t-2)^(2) ] dt` के लिये उच्चिष्ठ एवं निम्निष्ठ को जांचिये
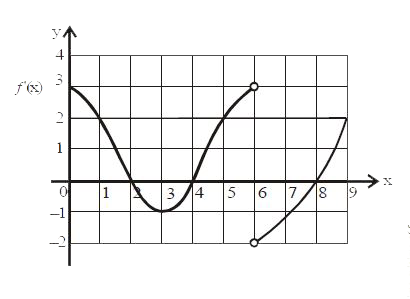
View Solutionसंतत् फलन के अवकलज का आरेख दर्शाया गया है तथा `f(0)=0` है। यदि
(i) f अन्तराल `[a,b)uu(c,d) uu(e,f]` में एकदिष्ट वर्धमान तथा `(p,q) uu(r,s)` में ओसमान है
(ii) का स्थानीय निम्निष्ठ `x=x_(1)` तथा `x = x_(2)` पर है
(iii) `f.(l,m) uu(n,t]` में उर्ध्वमुखी है
(iv) का नतिपरिवर्तन बिन्दु x=k है
(v) y= (x) के क्रान्तिक बिन्दुओं की संख्या 'w है।
तो `(a+b+c+d+e)+(p+q+r+s)+(l+m+n)+(x_(1)+x_(2))+(k+w)` का मान ज्ञात कीजिए |
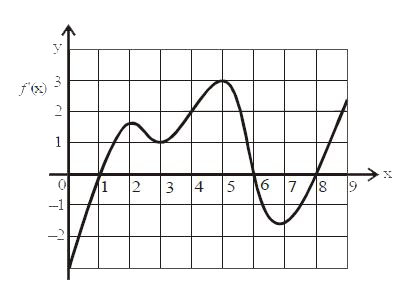
View Solutionसंतत् फलन के अवकलज का आरेख दर्शाया गया है तथा F (0) = 0 है :
(i) किस अन्तराल में वर्धमान या ओसमान होगा?
(ii) x के किन मानों पर स्थानीय उच्चिष्ठ या निम्निष्ठ होगा?
(iii) किस अन्तराल में उर्ध्वमुखी या अधोमुखी होगा?
(iv) नति परिवर्तन बिन्दुओं के निर्देशांक ज्ञात कीजिए।
(v) f(0)=0 को मानते हुए का आरेख खींचिए
View Solutionएक p परिमाप की खिड़की जिसका आधार एक चाप है एक आयत व एक अर्द्धवृत्ताकार भाग से बनी हुई है। अर्द्धवृत्ताकार भाग में रंगीन शीशा लगा है जबकि आयताकार भाग में पारदर्शी शीशा लगा है। पारदर्शी शीशा, रंगीन शीशा की अपेक्षा तीन गुना प्रकाश प्रति वर्ग मीटर पहुंचाता है। आयत की भुजाओं का अनुपात क्या होना चाहिए ताकि खिड़की अधिकतम प्रकाश पहुँचा सके?
View Solutionवक्र `ax^(2)+2bxy+ay^(2)=c,c gt b gt a gt 0` पर स्थित उन बिन्दुओं को ज्ञात कीजिए जिनकी मूल बिन्दु से दूरी न्यूनतम है।
View Solution
EXERCISE-04 [A] (CONCEPTUAL SUBJECTIVE EXERCISE) questions and complete solutions for chapter MAXIMA-MINIMA of ALLEN HINDI of Class 12
All Exercises from ALLEN HINDI Class 12 MATHS MAXIMA-MINIMA
- DO YOURSELF -1
- DO YOURSELF -2
- DO YOURSELF -3
- DO YOURSELF -4
- DO YOURSELF -5
- DO YOURSELF -6
- DO YOURSELF -7
- EXERCISE-01 (CHECK YOUR GRAPS)
- EXERCISE-01 (CHECK YOUR GRAPS) (सही विकल्पों को चुनिए (एक या एक से अधिक सही उत्तर हैं))
- EXERCISE-02 (BRAIN TEASERS) (सही विकल्पों को चुनिए (एक या एक से अधिक सही उत्तर हैं))
- EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) (कथन एवं कारण)
- EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) (गद्यांश आधारित प्रश्न) गद्यांश-I
- EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) (स्तम्भ सुमेलन)
- EXERCISE-04 [A] (CONCEPTUAL SUBJECTIVE EXERCISE)
- EXERCISE-04 [B] (BRAIN STORMING SUBJECTIVE EXERCISE)
- EXERCISE-05 [A] JEE-[MAIN] (PREVIOUS YEAR QUESTIONS)
- EXERCISE-05 [B] JEE-[ADVANCED] (PREVIOUS YEAR QUESTIONS)
- उदाहरण