Complete Solutions to Exercise - 05 B of chapter DEFINITE INTEGRATION of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | DEFINITE INTEGRATION |
| ALLEN HINDI | Exercise - 05 B |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
सिद्ध कीजिए कि `int_(e^(-1))^(e^(2))|(log_(e)x)/(x)|dx=(5)/(2)`
View Solutionयदि `g(x) = int_(0)^(x) f(t)dt` जबकि `1/2 le f(t) le 1 , t in [0,1]` तथा `0 le f(t) le 1/2 , t in [1,2]` के लिये, तब g(2)
View Solutionयदि `f(x)={{:(e^(cosx).sinx","|x|lt2),(2", "अन्यथा "):}` तब सिद्ध कीजिये कि `int_(-2)^(3)f(x)dx=2`
View Solution`xgt0` के लिए, माना `f(x)=int_(1)^(x)(lnt)/(1+t)dt` फलन `f(x)+f(1//x)` को ज्ञात कीजिए और दिखाइए कि `f(e)+f(1//e)=1//2` यहाँ `lnt=log_(e)t`
View Solution`int_(-pi/2)^(pi/2)(x^2cosx)/(1+e^(x))dx` का मान है
View Solutionमाना कि `f ,(0, +oo) to R` और `F(x) =underset(0)overset(x)intf (t) dt. ` यदि ` F(x^(2)) =x^(2)(1+x),` तो `f(4)=`
View Solutionमना कि `f(x) =underset(1)overset(x)intsqrt(2-t ^(2))dt, ` तो समीकरण `x^(2)-f' (x) =0` के वास्तविक मूल है
View Solutionमाना फलन f इस प्रकार है कि `f(-x)=-f(x),AAx inR` तथा `int_(0)^(1)f(x)dx=5`, तब `int_(-1)^(0)f(t)dt` का मान है
View Solutionसमाकलन `int_(-1/2)^(1/2)[[x]+ln((1+x)/(1-x))]dx` बराबर है
View Solutionयदि `I(m,n)=int_(0)^(1)t^(m)(1+t)^(n)dt,` तो `I(m+1,n-1)` के पदों में I(m,n) का व्यंजक है
View Solutionयदि फलन `f,f(x)=int_(x^(2))^(x^(2)+1)e^(-t^(2))dt` द्वारा परिभाषित है निम्न अंतराल में वर्धमान है
View Solutionयदि f एक सम फलन है, तो सिद्ध कीजिए कि
`int_(0)^(pi//2)f(cos2x)cosxdx=sqrt2int_(0)^(pi//4)f(sin2x)cosxdx`
View Solutionसमाकल `int_(0)^(1)sqrt((1-x)/(1+x))dx` का मान है
View Solutionयदि f(x) अवकलनीय है और `int_(0)^(t^(2))xf(x)dx=(2)/(5)t^(5)` तो `f((4)/(25))` बराबर है
View Solutionयदि `y(x)=int_(pi^(2)//16)^(x^(2))(cosx.cossqrt(theta))/(1+sin^(2)sqrt(theta))d theta` हो तो `x=pi` पर `(dy)/(dx)` ज्ञात कीजिए।
View Solutionहल कीजिए
`int_(-pi//3)^(pi//3)(pi+4x^(3))/(2-cos(|x|+(pi)/(3)))dx`
View Solutionयदि `int_(sinx)^(1)(t^(2)f(t))dt=(1-sinx)` हो, तो `f((1)/(sqrt(3)))` का मान है -
View Solution`int_(-2)^(0)[x^(3)+3x^(2)+3x+3+(x+1)cos(x+1)]dx` का मान है
View Solution`intx^2cosx dx` को हल कीजिए-
View Solution10 से 12 नीचे दिए गए गद्यांश को ध्यानपूर्वक पढ़िए एवं पूछे गए प्रश्नो के उत्तर दीजिए :
यदि निश्चित समाकल निम्न सूत्र के द्वारा परिभाषित हो, `int_(a)^(b)f(x)dx=(b-a)/(2)(f(a)+f(b))`, तथा `c in (a,b)` के लिए अधिक यथार्थ मान ज्ञात करने के लिए `F(c )=(c-a)/(2)(f(a)+f(c ))+(b-c)/(2)(f(b)+f(c ))` का प्रयोग कीजिए तथा जब `c=(a+b)/(2)` तो `int_(a)^(b)f(x)dx=(b-a)/(4)(f(a)+f(b)+2f(c))`
`int_(0)^(pi//2)sinx dx` का मान होगा -
View Solution10 से 12 नीचे दिए गए गद्यांश को ध्यानपूर्वक पढ़िए एवं पूछे गए प्रश्नो के उत्तर दीजिए :
यदि निश्चित समाकल निम्न सूत्र के द्वारा परिभाषित हो, `int_(a)^(b)f(x)dx=(b-a)/(2)(f(a)+f(b))`, तथा `c in (a,b)` के लिए अधिक यथार्थ मान ज्ञात करने के लिए `F(c )=(c-a)/(2)(f(a)+f(c ))+(b-c)/(2)(f(b)+f(c ))` का प्रयोग कीजिए तथा जब `c=(a+b)/(2)` तो `int_(a)^(b)f(x)dx=(b-a)/(4)(f(a)+f(b)+2f(c))`
प्रत्येक `x in (a,b)` के लिए `f'(x)lt0` तथा बिन्दु c इस प्रकार है कि `altcltb` तथा (c,f(c)) वक्र पर स्थित वह बिन्दु है जिसके लिए F(c) उच्चतम हो तो f'(c) का मान होगा -
View Solution10 से 12 नीचे दिए गए गद्यांश को ध्यानपूर्वक पढ़िए एवं पूछे गए प्रश्नो के उत्तर दीजिए :
यदि निश्चित समाकल निम्न सूत्र के द्वारा परिभाषित हो, `int_(a)^(b)f(x)dx=(b-a)/(2)(f(a)+f(b))`, तथा `c in (a,b)` के लिए अधिक यथार्थ मान ज्ञात करने के लिए `F(c )=(c-a)/(2)(f(a)+f(c ))+(b-c)/(2)(f(b)+f(c ))` का प्रयोग कीजिए तथा जब `c=(a+b)/(2)` तो `int_(a)^(b)f(x)dx=(b-a)/(4)(f(a)+f(b)+2f(c))`
यदि f(x) एक बहुपद है तथा यदि प्रत्येक a लिए `lim_(t toa)(int_(a)^(t)f(x)dx-((t-a)/(2))(f(t)+f(a)))/((t-a)^(3))=0 `तो f(x) की अधिकतम घात होगी -
View Solution`(5050int_(0)^(1)(1-x^(50))^(100)dx)/(int_(0)^(1)(1-x^(50))^(101)dx)` का मान ज्ञात कीजिए।
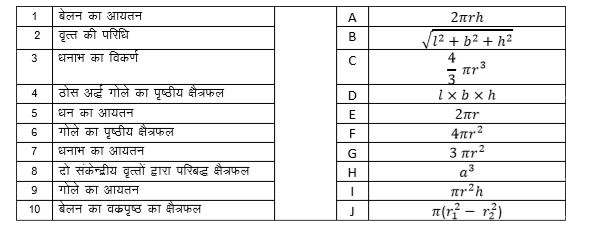
View Solutionसुमेलित कीजिए
View Solution`lim_(xto pi//4)(underset(2)overset(sec^(x)x)intf(t)dt)/(x ^(2)-(pi^(2))/(16))=`
View Solutionस्तम्भ -I में दिए गए समाकलों को स्तम्भ - II में दिए गए मानो से सुलमित कीजिए :

View Solutionमाना `S_(n)= sum_(k=1)^(n)(n)/(n^(2)+kn+k^(2)) ` एवं `T_(n) = sum_(k=0)^(n) (n)/(n^(2)+kn+k^2)` , n = 1, ,2, 3 ....... के लिए , तब
View Solutionमाना f, अन्तराल [0, 1] पर परिभाषित एक अऋणात्मक (non-negative) फलन है। यदि `int_(x)^(0)sqrt(1-{f'(t)}^(2))dt=int_(0)^(x)f(t)dt,0lexlt1` तथा f(0) = 0, तब
View Solutionयदि `I_(n) = int_(-pi)^(pi) (sinnx)/((1+pi^(x))sinx)dx` , n = 0 , 1, 2 ..........., तब
View Solutionमाना `f : R rarr R` एक सतत फलन है जो `f(x)=int_(0)^(x)f(t)` को संतुष्ट करता है | तब `f(log_(e)5)` का मान है
View Solution`underset(xrarr0)(lim)(1)/(x^(3))int_(0)^(x)(log(1+t))/(t^(4)+4)dt` का मान निम्न है-
View Solution`int_(0)^(1)(x^(4)(1-x)^(4))/((1+x^(2)))dx` का मान निम्न है-
View Solutionदिया है कि किसी वास्तविक संख्या x के लिए [x], अधिकतम पूर्णांक को दर्शाता है यदि अन्तराल `[-10,10]` पर वास्तविक मानो वाला फलन f निम्न प्रकार से परिभाषित है `f(x)={:{(x-[x]",","यदि [x] विषम है,"),(1+[x]-x","," यदि [x] सम है "):}` तो `(pi^(2))/(10)int_(-10)^(10)f(x)cospixdx` का मान है
View Solutionमाना कि अंतराल (-1,1) पर वास्तविक मानों वाला फलन f इस प्रकार परिभाषित है कि प्रत्येक `x epsilon (-1,1)` के लिए `e^(-x)f(x)=2+int_(0)^(x)sqrt(t^(4)+1)dt` तथा माना `f^(-1)` फलन f का प्रतिलोम है। तब `(f^(-1))’(2)` का मान निम्न है
View Solution`int_(sqrtlog2)^(sqrt(log3))(xsinx^(2))/(sinx^(2)+sin(log6-x^(2)))dx` का मान है
View Solutionयदि `y=e^(-x^(2)),y=0,x=0` और `x=1` द्वारा परिबद्ध क्षेत्र का क्षेत्रफल S है तो
View Solution`int_(-pi//2)^(pi//2) (x^(2)+log (pi+x)/(pi-x)) cos x dx` का मान ज्ञात कीजिए
View Solution`aepsilon R` (सभी वास्तविक संख्याओं का समुच्चय) `a!=-1` के लिए `lim_(nto oo)((1^(a)+2^(a)+…….+n^(a)))/((n+1)^(a-1)[(na+1)+(na+2)+……….+(na+n)])=1/60` तब `a=`
View Solution
Exercise - 05 B questions and complete solutions for chapter DEFINITE INTEGRATION of ALLEN HINDI of Class 12
All Exercises from ALLEN HINDI Class 12 MATHS DEFINITE INTEGRATION
- Do yourself - 1
- Do yourself - 2
- Do yourself - 3
- Do yourself - 4
- Do yourself - 5
- Do yourself - 6
- Do yourself - 7
- Do yourself - 8
- Exercise - 01 ( सही विकल्प चुनिए केवल एक सही उत्तर है)
- Exercise - 01 (सही विकल्पों के चुनिए एक या एक से अधिक सही उत्तर है)
- Exercise - 02 (सही विकल्पों को चुनिए एक या एक से अधिक सही उत्तर है)
- Exercise - 03 (कथन एवं कारण)
- Exercise - 03 (गद्यांश आधारित प्रश्न) गद्यांश 1
- Exercise - 03 (गद्यांश आधारित प्रश्न) गद्यांश 2
- Exercise - 03 (गद्यांश आधारित प्रश्न) गद्यांश 3
- Exercise - 03 (सत्य / असत्य)
- Exercise - 03 (स्तम्भ सुमेलन)
- Exercise - 04 A
- Exercise - 04 B
- Exercise - 05 A
- Exercise - 05 B
- उदाहरण