Complete Solutions to EXERCISE -3 MISCELLANEOUS TYPE QUESTIONS of chapter COMPLEX NUMBER of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | COMPLEX NUMBER |
| ALLEN HINDI | EXERCISE -3 MISCELLANEOUS TYPE QUESTIONS |
| Number Of Questions | 9 |
| Academic Year | 2023-24 |
निम्न प्रश्न में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है।स्तम्भ-I (Column-I) के वक्तव्यों को A,B,C तथा D नामित किया गया है जबकि स्तम्भ-II (Column-II) के वक्तव्यों को p,q,r तथा s नामित किया गया है। स्तम्भ-I (Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Column-II) के एक या एक से अधिक वक्तव्य (वक्तव्यों) से सही सुमेल करता है।
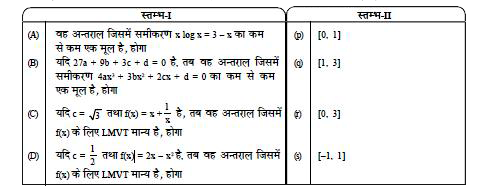
View Solutionकथन-I `|z-4-5i|=4` तथा `Arg(z-3-4i)=(pi)/4` को एक साथ संतुष्ट करने वाली केवल दो ही सम्मिश्र संख्यायों हैं। क्योंकि
कथन-II एक रेखा, वृत्त को अधिक से अधिक दो बिंदुओं पर काटती है।
View Solutionमाना `z_(1),z_(2),z_(3),|(z+2)/(z-1)|=2` को संतुष्ट करते है तथा `z_(0)=2` है। जब भी आवश्यक हो न्यूनतम धनात्मक कोणांक लें
वक्तव्य 1: `2arg((z_(1)-z_(3))/(z_(2)-z_(3)))=arg((z_(1)-z_(0))/(z_(2)-z_(0)))`
और
वक्तव्य -2 `z_(1),z_(2),z_(3),|z-z_(0)|=2` को संतुष्ट करते है।
View Solutionकथन I: यदि `z=i+2i^(2)+3i^(3)+…………+32i^(32)` हो तो `z,barz,-z` व `-barz` आर्गण्ड तल में वर्ग के शीर्ष है।
क्योंकि
कथन –II `z,barz,-z,-barz` आर्गण्ड तल पर मूल बिंदु से समान दूरी पर स्थित है।
View Solutionकथन-I यदि `z_(1)=9+5i` तथा `z_(2)=3+5i` तथा यदि `arg((z-z_(1))/(z-z_(2)))=(pi)/4` हो तो `|z-6-8i|=3sqrt(2)` होगा।
क्योंकि
कथन-II यदि z उस वृत्त पर स्थित है जिसके व्यास `z_(1)` तथा `z_(2)` हो तो `arg((z-z_(1))/(z-z_(2)))=(pi)/4` होगा।
View Solutionवक्तव्य 1 माना `z_(1),z_(2),z_(3)` तीन सम्मिश्र संख्यायें इस प्रकार है कि `|3z_(1)+1|=|3z_(2)+1|=|3z_(3)+1|` तथा `1+z_(1)+z_(2)+z_(3)=0` हो तो `z_(1),z_(2),z_(3)` सम्मिश्र तल में समबाहु त्रिभुज के शीर्षों को निरूपित करेंगे।
और
वक्तव्य 2: `z_(1),z_(2),z_(3)` समबाहु त्रिभुज के शीषो्रं को निरूपित करेंगें यदि `z_(1)^(2)+z_(2)^(2)+z_(3)^(2)=z_(1)z_(2)+z_(2)z_(3)+z_(3)z_(1)` हो।
View Solutionमाना z कोई एक सम्मिश्र संख्या है। `z^(n)-1` रूप के व्यंजक को गुण्नख्ण्डित करने के लिए, हम समीकरण `z^(n)=1` को लेंगें। इस समीकरण को डी-मॉयवर प्रमेय के प्रयोग से हल करेंगें। माना `1,alpha_(1),alpha_(2),……..alpha_(n-1)` इस समीकरण के मूल कै तो `z^(n)-1=(z-1)(z-alpha_(1))(z-alpha_(2))………….(z-alpha_(n-1))` होगा। व्यंजक `z^(n)-k^(n)` के गुणनखण्ड करने केलिए इस विधि को व्यापक किया जा सकता है।
उदाहरणः `z^(7)+1=prod_(m=0)^(6)(z-CiS((2mpi)/7+(pi)/7))`
इसको पुनः निम्न से सरलीकृत किया जा सकता है।
`z^(7)+1=(z+1)(z^(2)-2z"cos"(pi)/7+1)(z^(2)-2z"cos"(3pi)/7+1)(z^(2)-2z"cos"(5pi)/7+1)`………(i)
यह विभाजक गुणनखण्ड त्रिकोणमितीय सर्वसमिकाओं को सि8 करने में महत्वपूर्ण है। उदाहरण यदि समीकरण (i) में हम z=i रखे तो समीकरण (i) निम्न परिवर्तित होगी:
`(1-i)=(i+1)(-2i"cos"(pi)/7)(-2i"cos"(3pi)/7)(-2i"cos"(5pi)/7)`
अर्थात `"cos"(pi)/7"cos"(3pi)/7"cos"(5pi)/7=-18`
यदि व्यंजक `z^(5)-32` को रेखीय व द्विघात गुणनखण्डों में वास्वतिक गुणांकों के साथ लिखा जा सकता हो जैसे `(z^(5)-32)=(z-2)(z^(2)-pz+4)(z^(2)-qz+4)` जहां `pgtq` हो तो `p^(2)-2q` का मान होगा:
View Solutionमाना z कोई एक सम्मिश्र संख्या है। `z^(n)-1` रूप के व्यंजक को गुण्नख्ण्डित करने के लिए, हम समीकरण `z^(n)=1` को लेंगें। इस समीकरण को डी-मॉयवर प्रमेय के प्रयोग से हल करेंगें। माना `1,alpha_(1),alpha_(2),……..alpha_(n-1)` इस समीकरण के मूल कै तो `z^(n)-1=(z-1)(z-alpha_(1))(z-alpha_(2))………….(z-alpha_(n-1))` होगा। व्यंजक `z^(n)-k^(n)` के गुणनखण्ड करने केलिए इस विधि को व्यापक किया जा सकता है।
उदाहरणः `z^(7)+1=prod_(m=0)^(6)(z-CiS((2mpi)/7+(pi)/7))`
इसको पुनः निम्न से सरलीकृत किया जा सकता है।
`z^(7)+1=(z+1)(z^(2)-2z"cos"(pi)/7+1)(z^(2)-2z"cos"(3pi)/7+1)(z^(2)-2z"cos"(5pi)/7+1)`………(i)
यह विभाजक गुणनखण्ड त्रिकोणमितीय सर्वसमिकाओं को सि8 करने में महत्वपूर्ण है। उदाहरण यदि समीकरण (i) में हम z=i रखे तो समीकरण (i) निम्न परिवर्तित होगी:
`(1-i)=(i+1)(-2i"cos"(pi)/7)(-2i"cos"(3pi)/7)(-2i"cos"(5pi)/7)`
अर्थात `"cos"(pi)/7"cos"(3pi)/7"cos"(5pi)/7=-18`
`z^(5)+1` के लिए गुणनखण्ड का प्रयोग करके `4"sin"(pi)/10"cos"(pi)/5` का मान होगा
View Solutionमाना z कोई एक सम्मिश्र संख्या है। `z^(n)-1` रूप के व्यंजक को गुण्नख्ण्डित करने के लिए, हम समीकरण `z^(n)=1` को लेंगें। इस समीकरण को डी-मॉयवर प्रमेय के प्रयोग से हल करेंगें। माना `1,alpha_(1),alpha_(2),……..alpha_(n-1)` इस समीकरण के मूल कै तो `z^(n)-1=(z-1)(z-alpha_(1))(z-alpha_(2))………….(z-alpha_(n-1))` होगा। व्यंजक `z^(n)-k^(n)` के गुणनखण्ड करने केलिए इस विधि को व्यापक किया जा सकता है।
उदाहरणः `z^(7)+1=prod_(m=0)^(6)(z-CiS((2mpi)/7+(pi)/7))`
इसको पुनः निम्न से सरलीकृत किया जा सकता है।
`z^(7)+1=(z+1)(z^(2)-2z"cos"(pi)/7+1)(z^(2)-2z"cos"(3pi)/7+1)(z^(2)-2z"cos"(5pi)/7+1)`………(i)
यह विभाजक गुणनखण्ड त्रिकोणमितीय सर्वसमिकाओं को सि8 करने में महत्वपूर्ण है। उदाहरण यदि समीकरण (i) में हम z=i रखे तो समीकरण (i) निम्न परिवर्तित होगी:
`(1-i)=(i+1)(-2i"cos"(pi)/7)(-2i"cos"(3pi)/7)(-2i"cos"(5pi)/7)`
अर्थात `"cos"(pi)/7"cos"(3pi)/7"cos"(5pi)/7=-18`
यदि व्यंजक `z^(5)-32` को रेखीय व द्विघात गुणनखण्डों में वास्वतिक गुणांकों के साथ लिखा जा सकता हो जैसे `(z^(5)-32)=(z-2)(z^(2)-pz+4)(z^(2)-qz+4)` जहां `pgtq` हो तो `p^(2)-2q` का मान होगा:
View Solution
EXERCISE -3 MISCELLANEOUS TYPE QUESTIONS questions and complete solutions for chapter COMPLEX NUMBER of ALLEN HINDI of Class 12
All Exercises from ALLEN HINDI Class 12 MATHS COMPLEX NUMBER
- DO YOURSELF 1
- DO YOURSELF 2
- DO YOURSELF 3
- DO YOURSELF 4
- DO YOURSELF 5
- DO YOURSELF 6
- DO YOURSELF 7
- DO YOURSELF 8
- DO YOURSELF 9
- EXERCISE -01 (सही विकल्प चुनिए)
- EXERCISE -02 (सही विकल्प चुनिए)
- EXERCISE -3 MISCELLANEOUS TYPE QUESTIONS
- EXERCISE -5 (A) JEE (MAIN) : PREVIOUS YEAR QUESTIONS
- EXERCISE 4 (A) CONCEPTUAL SUBJECTIVE EXERCISE
- EXERCISE 4 (B) Brain storming subjective exercise
- EXERCISE 5 (B) JEE (ADVANCED) : PREVIOUS YEAR QUESTIONS
- उदाहरण
- विविध उदाहरण