Complete Solutions to Do yourself of chapter VECTORS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | VECTORS |
| ALLEN HINDI | Do yourself |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
यदि `vec(a)=2hati+mu hatj-7hatk` तथा `vec(b)=lambda hati+sqrt(3)hati-7hatk` दो समान सदिश हो, तो `lambda^(2)+mu^(2)` का मान ज्ञात कीजिए |
View Solutionयदि `vec(a),vec(b)` दो सदिश हो, तो निम्न में से कौनसा कथन सत्य होगा
View Solutionयदि सदिश ` veca, vec b ,vec c ` किसी त्रिभुज की भुजाओं द्वारा एक क्रम में प्रदर्शित हो, तो सिद्ध कीजिए की ` vec a + vec b + vec c =vec 0`
View Solutionयदि `vec(PO) + vec(OQ) = vec(QO) + vec(OR)`, तो दिखाइए कि P Q, R संरेखी हैं।
View Solutionकिसी दो सदिश `vec(a)` तथा `vec(b)` के लिए सिद्ध कीजिए कि
(a) `|vec(a)+vec(b)|le |vec(a)|+|vec(b)|`
(b) `|vec(a)-vec(b)|le|vec(a)|+|vec(b)|`
( c ) `|vec(a)+vec(b)|ge |vec(a)|-|vec(b)|`
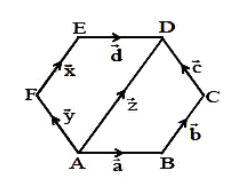
View Solutionदिये गये चित्र में (शीर्ष A, B, C, D, E, F सभी स्थिर है) कौन से सदिश:
View Solutionयदि `vec(a)=2hati-3hatj+4hatk` तथा `vec(b)=8hati-12hatj+16hatk` इस प्रकार है कि `vec(a)=lambda vec(b)` हो, तो `lambda` का मान ज्ञात कीजिए |
View Solutionयदि `3vec(a)+2vec(b)=5vec(c)` तथा `8vec(a)-7vec(b)=4vec(c)` हो, तो निम्न में से कौनसा कथन सत्य होगा
View Solutionउस बिन्दु के स्थिति सदिश ज्ञात कीजिए जो बिन्दु `2vec(a)-3vec(b)` तथा `3vec(a)-2vec(b)` को जोड़ने वाली रेखा को 2 : 3 अनुपात में अन्त: तथा बाह्य विभाजित करता है |
View SolutionABCD समान्तर चतुर्भुज है तथा P इसके विकर्ण का प्रतिच्छेद बिन्दु है | यदि O मूल बिन्दु है, तो प्रदर्शित कीजिए कि `vec(OA)+vec(OB)+vec(OC)+vec(OD)=4vec(OP)` होगा |
View Solution`3hati-6hatj+2hatk` की दिशा में इकाई सदिश ज्ञात कीजिए |
View Solutionबिन्दु P, Q, R के स्थिति सदिश क्रमश: `hati+2hatj+3hatk,-2hati+3hatj+5hatk` तथा `7hati-hatk` है | सिद्ध कीजिए कि P, Q तथा R समरेखीय है |
View Solutionदो सदिश `vec(a)` तथा `vec(b)` जिनके परिमाण क्रमश: 2 तथा 1 है तथा `vec(a).vec(b)=sqrt(3)` है, के मध्य कोण ज्ञात कीजिए |
View Solution`(vec(a)+3vec(b)).(2vec(a)-vec(b))` का मान ज्ञात कीजिए, यदि `vec(a)=hati+hatj+2hatk,vec(b)=3hati+2hatj-hatk` हो |
View Solutionसदिशों `2hati+4hatj-5hatk` तथा `lambda hati+2hatj+3hatk` के योग के अनुदिश इकाई सदिश का सदिश `hati+hatj+hatk` के साथ अदिश गुणनफल 1 है, तो `lambda` ज्ञात कीजिए |
View Solutionसदिश `vec(a)=4hati-2hatj+hatk` का सदिश `vec(b)=3hati+6hatj+2hatk` पर प्रक्षेप ज्ञात कीजिए | `vec(a)` का `vec(b)` के अनुदिश तथा `vec(b)` के लम्बवत घटक ज्ञात कीजिए |
View Solutionसदिशों `vec(a)=hati+2hatj-2hatk` तथा `vec(b)=-3hati+6hatj+2hatk` के मध्य कोण अर्द्धक ज्ञात कीजिए |
View Solution`vec(p)=-hati+hatj` तथा `vec(Q)=-hatj+hatk` को रखने वाले समतल में सदिश `vec(r)` इस प्रकार ज्ञात कीजिए कि `vec(r),vec(p)` के लम्बवत हो तथा `vec(r).vec(q)=-2` हो |
View Solutionयदि `vec(a)xxvec(b)=vec(c)xxvec(d)" तथा "vec(a)xxvec(c)=vec(b)xxvec(d)`, तो दिखाएँ कि `(vec(a)-vec(d)),(vec(b)-vec(c))` के समान्तर है, यह दिया है कि `vec(a)ne vec(d)" तथा "vec(b)ne vec(c)`.
View Solution`vec(a)xx vec(b)` ज्ञात कीजिए, यदि `vec(a)=2hati+hatk` तथा `vec(b)=hati+hatj+hatk` हो |
View Solutionकिन्हीं दो सदिश `vec(u)` तथा `vec(v)` के लिए, निम्न सिद्ध कीजिए
(a) `(vec(u).vec(v))^(2)+|vec(u)xx vec(v)|^(2)=|vec(u)|^(2)|vec(v)|^(2)`
(b)` (1+|vec(u)|^(2))(1+|vec(v)|^(2))=(1-vec(u).vec(v))^(2)+|vec(u)+vec(v)+(vec(u)xx vec(v))|^(2)`
View Solutionनिम्न रेखाओं के मध्य न्यूनतम दूरी ज्ञात कीजिए
`vec(r_(1))=(hati+2hatj+3hatk)+lambda(2hati+3hatj+4hatk)` तथा `vec(r_(2))=(2hati+4hatj+5hatk)+mu(3hati+4hatj+5hatk)`
View Solutionयदि `vec(a),vec(b),vec(c)` तीन असमतलीय परस्पर लम्बवत इकाई सदिश है, तो `[vec(a),vec(b),vec(c)]` ज्ञात कीजिए |
View Solutionयदि सदिश `vec(r),vec(a)+vec(b)+vec(c)` के लम्बवत है, जहाँ `[vec(a)vec(b)vec(c)]=z` तथा `vec(r)=l(vec(b)xx vec(c))+m(vec(c)xx vec(a))+m(vec(a)xx vec(b))` हो, तो `l+m+n` का मान ज्ञात कीजिए |
View Solutionसमान्तर षट्फलक का आयतन ज्ञात कीजिए जिसकी आसन्न कोरे `vec(a)=2hati-3hatj+4hatk,vec(b)=hati+2hatj-hatk` तथा `vec(c)=3hati-hatj+2hatk` है |
View Solutionज्ञात कीजिए कि सदिश `vec(a)=2hati+3hatj+2hatk, vec(b)=hati-hatj+2hatk` तथा `vec(c)=3hati+2hatj-4hatk` दक्षिणावर्त पेंच निकाय या वामावर्त पेंच निकय बनाते है |
View Solutionतीन सदिशों `vec(u),vec(v),vec(w)` के लिए निम्न में से कौनसा व्यंजक अन्य तीन के समान नहीं है
View Solutionयदि `vec(a)=2hati-4hatj+7hatk,vec(b)=3hati+5hatj-9hatk` तथा `vec(c)=hati+hatj+hatk` हो, तो `[vec(a)vec(b)vec(c)]` तथा `vec(a)xx(vec(b)xx vec(c))` का मान ज्ञात कीजिए |
View Solutionयदि `vec(p)=(vec(b)xx vec(c))/([vec(b)vec(c)vec(a)]),vec(q)=(vec(c)xx vec(a))/([vec(c)vec(a)vec(b)]),vec(r)=(vec(a)xx vec(b))/([vec(a)vec(b)vec(c)])` हो, तो `(vec(a)+vec(b)).vec(p)+(vec(b)+vec(c)).vec(q)+(vec(c)+vec(a)).vec(r)` का मान ज्ञात कीजिए |
View Solutionसदिशों का समुच्चय ज्ञात कीजिए जो समुच्चय `2hati+3hatj-hatk,hati-hatj-2hatk` तथा `-hati+2hatj+2hatk` के व्युत्क्रम है | अत: सिद्ध कीजिए कि `vec(a).vec(a)'+vec(b).vec(b)'+vec(c).vec(c)'=3` होगा |
View Solutionयदि `vec(a),vec(b)` तथा `vec(c)` अशून्य, असमतलीय सदिश है, तो जाँच कीजिए कि सदिश `vec(r_(1))=2vec(a)-3vec(b)+vec(c),vec(r_(2))=3vec(a)-5vec(b)+2vec(c)` तथा `vec(r_(3))=4vec(a)-5vec(b)+vec(c)` रेखीय स्वंतत्र या आश्रित है |
View Solutionएक कण पर कार्यरत बल `vec(F)=4hati+hatj-3hatk` उसे बिन्दु `hati+2hatj-3hatk` से बिन्दु `5hati+3hatj-4hatk` पर विस्थापित करता है, तो बल `vec(F)` द्वारा किया गया कार्य ज्ञात कीजिए |
View Solution
Do yourself questions and complete solutions for chapter VECTORS of ALLEN HINDI of Class 12