Complete Solutions to PROBLEM of chapter NUCLEI of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | NUCLEI |
| AAKASH SERIES | PROBLEM |
| Number Of Questions | 42 |
| Academic Year | 2023-24 |
Compare the radii of the nuclei of mass numbers 27 and 64.
View SolutionHow many electrons, protons and neutrons are there in 12g of `._6C^12` and in 14g of `._6C^14` ? (Take Avogadro number `N=6xx10^23` )
View SolutionCalculate the mass defect, binding energy and binding energy per nucleon of an alpha particle ? (An `alpha`- particle is nothing but helium nucleus. Hence its symbol is `._2He^4`. It contains 2 protons, 2 neutrons with a mass number 4. Mass of hydrogen atom `m_H`= 1.007825 u, Mass of neutron `m_n` = 1.008665 u, Atomic number of helium Z = 2, Mass number of helium A = 4, Mass of helium atom `m_n` = 4.00260 u.)
View SolutionCalculate the binding energy of an `alpha`-particle. Given that mass of proton = 1.0073 u, mass of neutron = 1.0087 u, and mass of `alpha`- particle = 4.0015 u.
View SolutionFind the average binding energy per nucleon of `._7N^14` and `._8O^16`. Their atomic masses are 14.008 u and 16.000 u. The mass of `._1H^1`atom is 1.007825 u and the mass of neutron is 1.008665 u. Which is more stable?
View SolutionThe binding energies per nucleon for deuteron `(._1H^2)` and helium `(._2He^4)` are 1.1 MeV and 7.0 MeV respectively. Calculate the energy released, when two deuterons fuse to form a helium nucleus.
View SolutionFind the Q value of the reaction `H^1+Li^7 to He^4 + He^4`. Determine whether the reaction is exothermic or endothermic? The atomic mass of `H^1, He^4` and `Li^7` are 1.007825 u, 4.002603 u and 7.016004 u respectively.
View SolutionCalculate the average energy required to extract a nucleon from the nucleus of an `alpha ` - particle ,proton and neutron are 4.00150 a.m.u 1.00728 a.m.u and 1.00867 amu respectively .
View SolutionFind the energy required to split `._(8)^(16)O` nucleus into four `alpha` - particles. The mass of an `alpha`- particle is 4.002603u and that of oxygen is 15.994915u.
View SolutionThe kinetic energy of `alpha` - particles emitted in the decay of `""_(88)Ra^(226)` into `""_(86)Rn^(222)` is measured to be 4.78 MeV. What is the total disintegration energy or the 'Q - value of this process ?
View SolutionHow many `alpha and beta ` - particles are emitted when uranium nucleus `(""_(92)^(238)U)` decay to `""_(82)^(214)Pb` ?
View SolutionNeon -23 decays in the following way `""_(10)^(23)Nerarr""_(11)^(23)Ne+""_(-1)e^0+barv.` Find the minimum and maximum kinetic energy that the beta particle `(""_(-1)e^(0))` can have . The atomic masses of `""^(23)Ne and ""^(23)Na ` are 22.9945 u and 22.9898 u, respectively.
View SolutionA radioactive sample has an activity of `4xx10^7` Ci. Express its activity in .becqueral. and .rutherford..
View SolutionFind the probability that a certain radioactive atom would get disintegrated in a time equal to the mean life of the radioactive sample.
View Solutionhe radioactivity of given sample of whisky due to tritium (Half life=12 yrs) was found to be only 3.125% of that measured in a recently purchased bottle marked "10 years old". By how many years ago the sample must have been prepared?
View SolutionThe half life of a substance is 20 minutes. E The time interval between 33% decay and 67% decay.
View SolutionFind the number of half lives elapsed, before which, 93.75% of a radioactive sample has decayed.
View SolutionCalculate the number of half lives elapsed, the end of which, the activity of a radioactive sample decrease by 90%.
View SolutionEstimate the number of mean lives elapsed, when the number of atoms in a radioactive sample decrease to 5% of the original value.
View SolutionThe mean lives of a radioactive substance are 1620 year and 405 year for `alpha`-emission and `beta`-emission respectively. Find the time during which three - forth of a sample will decay if it is decayed both by `alpha` -emission and `beta`-emission simultaneously.
View SolutionA radioactive isotope X has a half life of 3 second Initially a given sample of this isotope contains 8000 atoms. Calculate (a) its decay constant , (b) the time `t_1` when 1000 atoms of the isotope X remain in the sample , and (c) the number of decay per second in the sample at `t =t_1`.
View Solutionn alpha particles per second are emitted from N atoms of a radioactive element. Then find the half life of radioactive element ?
View SolutionFour vessels A,B,C and D contain respectively 20g atom (`T_(1//2)` = 5h) 2g atom (`T_(1//2)`=1h) 5g atom (`T_(1//2)` = 2h) and 10g atom (`T_(1//2)` = 3h) of different radio nuclides in the 12 beginning, the maximum activity would be exhibited by the vessel is
View SolutionAt time t = 0 , number of nuclei of a radioactive substance is 100. At t = 1 s this number becomes 90. Find the number of nuclei at t = 2s.
View SolutionThe activity of a sample of radioactive material is `A_1` at time `t_1 and A_2` at time `t_(2)(t_2 gt t_1)` . Obtain an expression for its mean life.
View SolutionThe half- life of `.^238U` for `alpha`-decay is `4.5xx10^19` years. How many disintegrations per second occur in 1g of `.^238U` ? (Avogadro.s number = `6.023 xx 10^23 "mol"^(-1)` )
View SolutionA radioactive substance has `6.0 xx 10^18` active nuclei initially. What time is required for the active nuclei o the same substance to become `1.0 xx 10^18` if its half-life is 40 s.
View SolutionTwo radioactive substances X and Y initially contain equal number of atoms. Their half-lives are 1 hour and 2 hours respectively. Calculate the ratio of their rates of disintegration after four hours.
View SolutionA radioactive sample can decay by two different processes. The half-life for the first process is `T_1` and that for the second process is `T_2` Find the effective half - life T of the radioactive sample.
View SolutionThe count rate from `100 "cm"^2` of a radioactive liquid is c. Some of this liquid is now discarded. The count rate of the remaining liquid is found to be c/10 after three half-lives. Find the volume of the remaining liquid, in `"cm"^3` ?
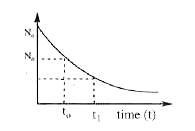
View SolutionGraph shows the variation of the number of radioactive atoms left undecayed with time. Find the time corresponding to `N=N_0//3` ?
View SolutionThe activity of a certain radioactive sample is plotted against time in graph. If the initial slope of the curve is m, then find the slope of the curve at point P ?
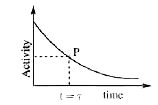
View SolutionA nuclear power reactor generates electric power of 100 MW. How many number of fissions occur per second if nuclear fuel used in the reactor is uranium ?
View SolutionHow much `.^235U` is consumed in a day in an atomic power house operating at 400 MW, provided the whole of mass `.^235U` is converted into energy?
View SolutionIf the speed of light were 2/3 of its present value, what would be fractional decrease in the energy released in a given atomic explosion
View SolutionCalculate the energy released by the fission 1 g of `.^235U` in joule, given that the energy released per fission is 200 MeV. (Avogadro.s number =`6.023xx10^23` )
View SolutionCalculate the energy released by fission from 2g of `._(92)^(235)U` in kWh. Given that the energy released per fission is 200 MeV.
View SolutionA reactor is developing nuclear energy at a rate of 32,000 kilowatt. How many kg of `U^235` undergo fission per second? How many kg of `U^235` would be used up in 1000 hour of operation? Assume an average energy of 200 MeV released per fission? Take Avogadro.s number as `6 xx 10^23` and 1 MeV =`1.6xx10^(-13)` joule
View SolutionIn the process of nuclear fission of 1 gram uranium, the mass lost is 0.92 milligram. The efficiency of power house run by it is 10%. To obtain 400 megawatt power from the power house, how much uranium will be required per hour? `(c=3xx10^8 "ms"^(-1))`
View Solution(a) Are the equations of nuclear reactions balanced in the sense a chemical reaction?
(b) If both the number of protons and the number of neutrons are conserved in each nuclear reaction, in what way is mass converted into energy (or vice-versa) in a nuclear reaction?
View SolutionAn electron-positron pair is produced when a `gamma`-ray photon of energy 2.36MeV passes close to a heavy nucleus. Find the kinetic energy carried by each particle produced, as well as the total energy with each.
View SolutionA gamma ray photon of energy 1896 MeV annihilates to produce a proton-antiproton pair. If the rest mass of each of the particles involved be 1.007276 a.m.u approximately, find how much K.E these will carry?
View Solution
PROBLEM questions and complete solutions for chapter NUCLEI of JEE (MAIN AND ADVANCED) PHYSICS of Class 12