Complete Solutions to EXAMPLES of chapter CURRENT ELECTRICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CURRENT ELECTRICITY |
| AAKASH SERIES | EXAMPLES |
| Number Of Questions | 66 |
| Academic Year | 2023-24 |
The number of electrons striking the screen of CRT is `7.5xx10^(15)` in 10 s. Calculate the electric current.
View SolutionIn a hydrogen atom, electron moves in an orbit of radius `5 xx 10^(-11)` m with a speed of `2.2xx10^6` m/s . Calculate the equivalent current.
View SolutionA rectangular block has dimensions 5 cm `xx ` 5 cm `xx 10 cm ` . Calculate the resistance measured between (a) two square ends and (b) the opposite rectanglar ends specific resistance of the material is `3.5xx10^(-5)` `Omega` m
View SolutionTwo wires of same material have their lengths in the ratio 2:3 and radii 8:9 . Equal value of p.d is applied between their ends (separately). Calculate the ratio of current through those two
View SolutionTwo wires of equal diameters of resistivities `p_1 and p_2` and length` x_1` and `x_2` respectively are joined in series. The equivalent resistivity of the combination is
View SolutionA long round conductor of cross- sectional area S is made of material whose resistivity depends only on distance r from the axis of the conductor as `rho = (alpha)/(r^2)` , where `alpha` is a constant. Find (a) the resistance per unit length of such a conductor .
(b) the electric field strength in the conductor due to which a current i flows through it .
View SolutionA wire of silver has a resistance of 1 ohm. Specific resistance of constantan is 30 times the specific resistance of silver. Find the resistance of a constantan wire whose length is one third length of the silver wire and radius half the radius of the silver wire.
View SolutionA currrent of 5A is passing through a metallic wire of cross sectional area `14xx 10^(-6) m^2` . If the density of the charge carries in the wire is `5 xx 10^(26)//m^3`, find the drift speed of the electrons (charge carries).
View SolutionPotential difference of 100 V is applied to the ends of a copper wire one metre long. Calculate the average drift velocity at `27^@ C` . Assume that there is one conduction electron per atom. The density of copper is `9.0xx10^3 kg//m^3` , Atomic mass of copper id 63.5 g. Avogadro's number `=6.0xx10^(23)` per gram- mole. Conductivity of copper is `5.81xx10^(7) Omega^(-1)` . Boltzmann constant `=1.38xx10^(-23) JK^(-1)` .
View SolutionThe temperature coefficient of resistance of a wire is `0.00125^@ C^(-1)` w.r.t temperature at 300 K at which the resistance of the wire is one ohm. Find the temperature at which the resistance of the wire will be 2 ohm.
View SolutionA wire has a resistance of `2.5 Omega ` at `100^@` C. Temperature coefficient of resistance of the material `alpha = 3.6 xx 10^(-3) K^(-1) ` at `25^@` C. Find its resistance at `25^@ C`.
View SolutionThe temperature coefficient of resistance of platinum is `alpha=3.92xx10^(-3)K^(-1)` at `0^(@)C`. Find the temperature at which the increase in the resistance of platinum wire is `10%` of its value of `0^(@)C`.
View SolutionThe temperature coefficient of resistivity of material is 0.0004/k. When the temperature of the material is increased by `50^(@)C`, its resistivity increases by `2xx10^(-8)` ohm-m. The initial resistivity of the material in olm-m is
View SolutionA total of `6.0xx10^(16)` electrons pass through any cross - section of a conducting wire per second. Find the current.
View SolutionCalculate the drift speed of electrons when 1A of current flows in a copper wire of cross section 2 `"min"^2` . The number of free electrons in `1 cm^3` of copper is `8.5 xx 10^(22)`.
View SolutionTwo wires A and B of same mass and material are taken. Diameter of wire A is half of wire B. If resistance of wire A is `24Omega` find the resistance of wire B.
View SolutionTwo electric bulbs have their resistances in the ratio 2:3 . They are connected (a) first in series and then (b) in parallel across the same voltage . Find the ratio of powers consumed by each of the two bubls in the two combinations.
View SolutionTwo electric lamps of 40 W each are connected in parallel across the mains supply. Find the total power consumed by the two bulbs together.
View SolutionThree equal resistors connected in series across a source of e.m.f. together dissipate 10 W power. Find the power dissipated if the same resistors are connected in parallel.
View SolutionTwo heater coils separately take 10 minutes and 5 minutes to boil a certain amount of water. Find the time taken by both the coils connected in series to boil the same amount of water .
View SolutionTen 50 W bulbs are operated on an average for 10 hours a day. Find the energy consumed in kWH in one month of 30 days.
View SolutionAn electric bulb is rated 220 V and 100 W. When it is operated on 110 V, the power consumed will be –
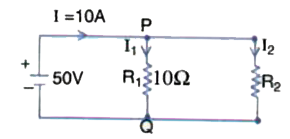
View SolutionFor a circuit shown in Fig. find the value of resistance `R_2` and current `I_2` flowing through `R_2`
View SolutionFind the equivalent resistance of the network in fig. between points A and B .
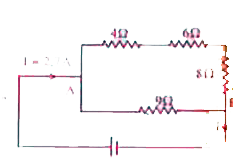
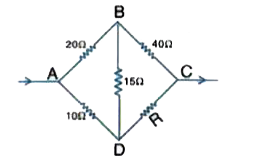
View SolutionFind the equivalent resistance of the network in fig. between points A and C.

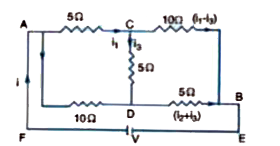
View SolutionFind potential difference between points A and B of the network shown in Fig. and distribution of given main current through different resistors.
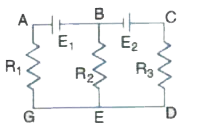
View SolutionConsider thr network as shown in fig. Current is supplied to the network by two batteries as shown. Find the values of currents `I_1 , I_2, I_3` . The direction of the currents are as indicated by the arrows.
View SolutionFind the current in each cell considering circuit given in fig.
View SolutionIn the given circuit values are as follows
`epsi_1 = 2V, epsi_2 = 4V, R_1 = 1 Omega and R_2 = R_3 = 1 Omega`
Calculate the currents through `R_1 , R_2 and R_3`
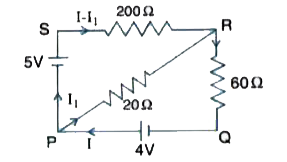
View SolutionIn the given circuit , the two cells have no internal resistance. Calculate the potential difference across the `20 Omega` resistor .
View SolutionFind the equivalent resistance between the points A and B of the circuit shown in the fig.
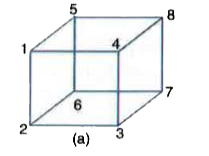
View SolutionTwelve equal wires , each of resistance r ohm are connected so as to form a skeleton cube. Find the equivalent resistance between the diagonally opposite points 1 and 7.
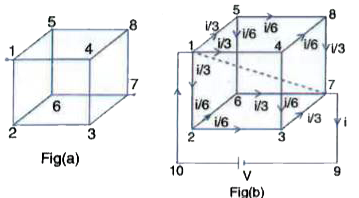
View SolutionTwelve equal wires each of resistance r are joined to form a skeleton cube. Find the equivalent resistance between two corners on the same edge of the cube.
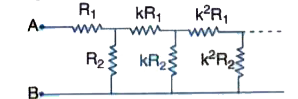
View SolutionThe circuit diagram shown in fig consists of a very large (infinite) number of elements . The resistances of the resistors in each subsequent element differ by a factor k from the resistance of the resistors in the previous element. Determine the resistance `R_(AB)` between points A and B if the resistances of the first element are `R_1 and R_2`
View SolutionFind the value of R in fig. so that there is no current in the 15 `Omega` resistor
View SolutionIn a metre bridge , the null point is found at a distance of 33.7 cm from A. If now a resistance of `10 Omega` is connected in parallel with S, the null point occurs at 51.9 cm. determine the values of R and S.
View SolutionA balance point in a meter bridge experiment is obtained at 30 cm from the left. If right gap contains `3.5 Omega` , what is the resistance in the left gap ?
View SolutionWhen a current drawn from a battery is 0.5 A, its terminal potential difference is 20 V. And when current drawn from it is 2.0 A , the terminal voltage reduces to 16 V . Find out e.m.f and internal resistance of the battery.
View SolutionWhen a battery is connected to the resistance of `10Omega` the current in the circuit is 0.12 A. The same battery gives 0.07A current with `20Omega` Calculate e.m.f. and internal resistance of the battery.
View SolutionA cell on open circuit has e.m.f 2.0 V and in closed circuit having current of 0.05 A , the p.d is 1.5 V . Calculate internal resistance of the cell.
View SolutionA battery of e.m.f 6 V and internal resistance `1 Omega` gives a p.d of 5.8 V when connected to a resistance . Find the external resistance .
View SolutionAn ideal battery passes a current of 5A through a resistor . When it is connected to another resistance of `10 Omega` in parallel, the current is 6A . Find the resistance of the first resistor.
View SolutionTwo batteries A and B each of e.m.f. 2V are connected in series to an external resistance `R = 1 Omega`. If the internal resistance of battery A is `1.9 Omega` and that of B is `0.9 Omega`. What is the potential difference between the terminals of battery A ?
View SolutionWhen a resistance of 11 `Omega` is connected in series with an electric cell, 0.5 A current flows thrugh it . If the 11 `Omega` resistor is replaced by `5 Omega` resistor the current flowing through it is 0.9 A . Find the internal resistance of the cell.
View SolutionTwo cells A and B with same e.m.f. of 2 V each and with internal resistance `r_A = 3.5 Omega` and `r_B = 0.5 Omega` are connected in series with an external resistance R =` Omega R ` Find the terminal voltages across the two cells.
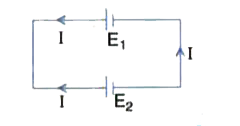
View SolutionTwo cells of e.m.f. 's `E_1 and E_2 ` are connected in series in a circuit . Let `r_1 and r_2` be the internal resistance of the cells. Find the current through the circuit.

View SolutionLet two cells of e.m.f.'s `E_1 and E_2` be connected in parallel in a circuit . Let `r_1 and r_2` be the internal resistances of the cells . Find the value of the current
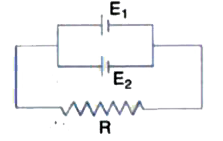
View SolutionLet two cell of e.m.f's `E_1 and E_2` and internal resistances `r_1 and r_2` be connected in parallel to a circuit with an external resistance R. Find the value of the current I through the given resistor .
View SolutionAn electric current is passed through a circuit containing two wires of the same material, connected in parallel. The lengths of the wires are in the ratio of 4:3 and radii of the wires are in the ratio of 2:3 . Find the ratio of the currents passing through the wires.
View SolutionTwelve cells each having the same emf are connected in series and are kept in a closed box. Some of the cells are wrongly connected . This battery is connected in series with an ammeter and two cells identical with each other . The current is 3A when the cells and battery aid each other and 2A when the cells and battery oppose each other . How many cells ae wrongly connected ?
View SolutionA cell is e.m.f 2V and internal resistance `1 Omega` is connected to a potentiometer of length 1m and resistance `4 Omega` Calculate the potential drop per cm.
View SolutionIn a potentiometer experiment the balancing length with a cell is 560 cm. When an external resistance of `10 Omega` is connected in parallel to the cell, the balancing length changes by 60 cm . Find the internal resistance of the cell.
View SolutionLength of potentiometer wire is 5 m. It is connected with a battery of fixed e.m.f Null point is obtained for Daniel cell at 100 cm on it. If the length of the wire is made 7 m, then what will be the position of null point ?
View SolutionIn a potentiometer experiment when a battery of e.m.f . 2 V is included in the secondary circuit, the balance point is at 500 cm . Find the balancing length from the same end when a cadmium cell is e.m.f 1.018V is connected to the secondary circuit.
View SolutionIn the secondary circuit of a potentiometer , a cell of internal resistance `1.5 Omega` gives a balancing length of 52 cm. To get a balancing length of 40 cm , how much resistance is to be connected across the cell ?
View SolutionA circuit having resistor of 2 mega-ohm and capacitor of `1 muF` is placed in series with a battery of 2 volt. Find the time after which the charge reaches 86.4% of its maximum value.
View SolutionA capacitor is being charged through a resistance of 3 mega ohm. If it reaches 75% of its final potential in 0.5 sec, find its capacitance.
View SolutionA capacitor, charged to 10 V , is being discharged through a resistance R. At the end of 1s the voltage across the capacitor is 5V. What will be the voltage after 2s ?
View SolutionA capacitor of capacitance C fared is being charged from a.d.c supply of E volts through a resistance of R ohms, i) Show that most of the voltage across the capacitor builds up during the first time constant . Ii) Show that capacitor is almost fully charged after time equal to 5 time constants.
View SolutionA `2muF` Capacitor is connected to a.d.c source of 100 volt through ` 1 M Omega` series resistance . Calculate time constant .
View SolutionA `2muF` Capacitor is connected to a.d.c source of 100 volt through ` 1 M Omega` series resistance . Calculate initial charging current .
View SolutionA `2muF` Capacitor is connected to a.d.c source of 100 volt through ` 1 M Omega` series resistance . Calculate initial rate of rise of p.d across the capacitor.
View SolutionA `2muF` Capacitor is connected to a.d.c source of 100 volt through ` 1 M Omega` series resistance . Calculate voltage across the capacitor 6 seconds after the application of voltage .
View SolutionA `2muF` Capacitor is connected to a.d.c source of 100 volt through ` 1 M Omega` series resistance . Calculate time taken for the capacitor to be fully charged.
View SolutionA resistor R and a `4muF` capacitor are connected in series across a 200 V d.c. supply. Across the capacitor is connected a neon lamp that strikes at 120 V in 5 seconds . Find R.
View SolutionA capacitor of `1 muF` and resistance `82 kOmega` are connected is series with a d.c. source of 100 volt. Calculate the magnitude of energy and the time in which energy stored in the capacitor will reach half of its maximum value.
View Solution
EXAMPLES questions and complete solutions for chapter CURRENT ELECTRICITY of JEE (MAIN AND ADVANCED) PHYSICS of Class 12