Complete Solutions to PROBLEMS ( LEVEL-II) of chapter RAY OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | RAY OPTICS |
| AAKASH SERIES | PROBLEMS ( LEVEL-II) |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
Two plane mirrors are combined to each other such that one is in y-z plane and the other is in X-z plane. A ray of light travelling along a vector `hati+ hati+ hatk` is incident on the first mirror. Find the unit vector in the direction of emergent ray after successive reflections through both the mirrors.
View SolutionFind the relationship between angle of incidence and angle of emergence of light in the adjacent figure. Are angle of incidence and angle of emergence equal?

View SolutionA bird looking down vertically into a pond from 12cm above the surface sees a fish apparently 18 cm below the surface. What is the actual depth of the fish? What is the apparent height of bird as seen by the fish? [Refractive index of water = 4/3]
View SolutionThere is a dust particle in a glass slab of thickness t and refractive index `mu =1.5`. When seen from one side of the slab, the dust particle appears at a distance 6 cm. From opposite side it appears at 4 cm. Find the thickness t of the glass slab.
View SolutionA parallel beam of light is incident on a rectangle transparent plate of thickness 8 cm. The angle of incidence and refraction of the beam is `60^@ and 30^@` respectively. Find the lateral shift.
View SolutionA pile 4 m high driven into th bottom of a lake is 1 m above the water. Determine the length of the shadow of the pile on the bottom of the lake if the sun rays make an angle `45^@` with the water surface. The refractive index of water is 4/3.
View SolutionA ray of light travelling in a rarer medium, strikes a plane boundary between the rarer medium and a denser medium at an angle of incident 'i' such that the reflected and the refracted rays are mutually perpendicular. Another ray of light of same frequency is incident on the same boundary from the side of denser medium. Find the minimum angle of incidence at the denser-rarer boundary so that the second ray is totally reflected.
View SolutionA small object of height 0.5 cm is placed in front of a convex surface of glass `( mu = 1.5)` of radius of curvature 10 cm. Find the height of the image formed in glass.
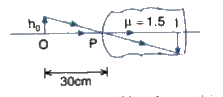
View SolutionA paperweight in the form of a hemisphere of radius 3.0 cm is used to hold down a printed page such that flat surface touch the paper. An observer looks at the page vertically through the paperweight. At what height above the page will the printed letters near the centre appear to the observer?
View SolutionA convex glass lens `( mu = 1.5 )` produces a real image of an object. The size of the image equals the size of the object. When the air surrounding the lens is replaced by a liquid, the size of the image is found to be twice that of the object. Find the refractive index of the liquid.
View SolutionTwo plano concave lenses of glass of refractive index 1.5 have radii of curvature of 20 and 30 cm. They are placed in contact with curved surfaces towards each other and the space between them is filled with a liquid of refractive index (4/3). Find the focal length of the system.
View SolutionA rectangular block of refractive index `mu` is placed on a printed page lying on a horizontal surface. Find the minimum value of `mu` so that the letters on the page is not visible from any of the vertical sides.
View SolutionThe dispersive power of crown and flint glasses are 0.03 and 0.05 respectively. If the difference in the refractive indices of blue and red colours are 0.015 for crown glass and 0.022 for flint glass, calculate the angles of the two prisms for a deviation 2° without dispersion.
View SolutionA thin prism of crown glass `(mu_r = 1.515,mu_v, = 1.525)` and a thin prism of flint glass `(mu_r = 1.612, mu_v = 1.632 )` are placed in contact with each other. Their refracting angles are `5.0^@` each and are similarly directed. Calculate the angular dispersion produced by the combination
View SolutionA beam of light converging towards a point O is intercepted by a convex mirror of focal length 30 cm. The point is 20 cm behind the mirror from its pole. Find the nature and position of the image. What if the point O is at distance 50 cm from the pole?
View SolutionWhen an object is placed at a distance of 25cm from a mirror, the magnification is `m_1`. The object is moved 15 cm farther away with respect to the earlier position, and the magnification becomes `m_2`. If `(m_1)/(m_2)` = 4, then calculate the focal length of the mirror.
View SolutionAn object is placed between a plane mirror and a convex mirror as shown, Let `I_1 and I_2` be the images formed by the plane mirror and the convex mirror respectively. It is found that distance between `I_1 and I_2` is 100 cm, distance between the object and `I_2` is 60 cm and has magnification 1/2. Find focal length of the convex mirror and also the distance between the two mirrors.
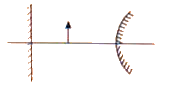
View SolutionA plane mirror and a concave mirror are arranged as shown in figure and O is a point object. Find the position of image formed after two reflections, first one taking place at concave mirror.

View SolutionDescribe the image in convex mirror, of the image of rod PQ in the plane mirror (radius of curvature of mirror is 60 cm).

View SolutionThe u-v curve in a concave mirror as shown in figure.

Find the focal length and power of the mirror.
View SolutionThe u-v curve in a concave mirror as shown in figure.

Find the nature and position of the image, when an object is placed at 15 cm from the mirror.
View SolutionOne face of a rectangular glass plate 6 cm thick is silvered. An object held 8 cm in front of the front face forms an image 12 cm behind the silvered face. Find the refractive index of glass.
View SolutionThe bottom of water tank is lined with a plane mirror.A particle is projected from the origin O under gravity. The equation of the trajectory is `y = a(x - x^2)`. The depth of the tank is 4a and this is completely filled. Find the distance of image with respect to mirror after reflection of rays from it.

View SolutionIn figure a point source S is placed at a height h above the plane mirror in a medium of refractive index `mu`.
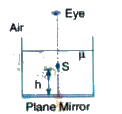
Find the distance between the images.
View SolutionConsider situation in figure. The bottom of the pot is reflecting plane mimor, Fis a small fish and is an object. Refractive index of water is `mu`. Find the distances from it self the fish can see the image (s) of the object O.
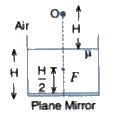
View SolutionA point source S is placed at a height h from the bottom of a vessel of height H(`lt` h) and area A. The vessel is polished at the base. Water is gradually filled in the vessel at a constant rate `alpha m^3//s`. Find how the distance d of image of the source from the bottom of the vessel varies with time t.

View SolutionA concave mirror of radius of curvature 40 cm is placed at the bottom of a tank of water` (mu = 4//3)` with its optic axis vertical and the mirror facing upward. Find the position of the image of a bird flying over the tank at a height 60 cm above the surface of water, which is 20 cm deep.
View SolutionThree different slabs consisting of different media are placed in front of a concave mirror of radius of curvature 150 cm. The whole arrangement is placed in water (`mu = 4//3`). An object O is placed at a distance 153 cm from the mirror. The refractive index of different media are given in the diagram. Find the position of final image formed by the system.

View SolutionA cylindrical vessel of depth 4m is fully filled with non homogenious liquid whose refractive index `(mu)` varies with depth y (in meters) a `mu=1+(y)/(4)`. Find the depth of the bottom of vessel as seen by an observer just above the top of the vessel.
View SolutionA point source is sinking down in a liquid of refractive index u with a constant velocity . Find the rate of change of the area through which light will escape from the liquid when the source is at a depth `h_0`
View SolutionA ray of light enters a glass slab from air as shown in figure. If refractive index of glass slab is given by `mu=A-Bt`, where A and B are constants and t is the thickness of slab measured from the top surface. Find the maximum depth travelled by ray in the slab. Assume thickness of slab to be sufficiently large.

View SolutionA hemisphere (made of material of refractive index `sqrt(3) )`of radius ris placed on a horizontal surface with its base touching the surface. A vertical beam of cross sectional radius `(sqrt(3))/(2) r `is incident symmetrically on its curved surface. Find the radius of the spot of light formed on the horizontal surface
View SolutionA beam of light converges at a point P. Now a lens is placed in the path of the convergent beam 12 cm from P. At what point does the beam coverage if the lens is
a convex lens of focal length 20 cm. and
View SolutionA beam of light converges at a point P. Now a lens is placed in the path of the convergent beam 12 cm from P. At what point does the beam coverage if the lens is
a concave lens of focal length 16 cm?
View SolutionThe distance between two point sources of light is 24 cm. Find out where you would place a converging lens of focal length 9 cm, so that the images of both the sources are formed at the same point.
View SolutionFocal length of a thin convex lens is 30 cm. At a distance of 10 cm from the lens there is a plane refracting surface of refractive index 3/2. Where will the parallel rays incident on lens converge ?
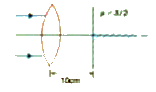
View SolutionBoth object and convex lens are approaching each other along the principal axis as shown. Find the speed of image relative to object at the given instant as shown in the figure.
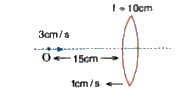
View SolutionA converging lens of focal length 12 cm and a diverging mirror of focal length 7.5 cm are placed 5.0 cm apart with their principal axes coinciding. Where should an object be placed so that its image falls on itself?
View SolutionA converging lens of focal length 15 cm and a converging mirror of focal length 10 cm are placed 50 cm apart with common principal axis. A point source is placed in between the lens and the mirror at a distance of 40 cm from the lens. Find the locations of the two images formed.
View SolutionA convex lens of focal length 15 cm and a concave mirror of focal length 30 cm are kept with their optic axis PQ and RS parallel but separated in vertical direction by 0.6 cm as shown. The distance between the lens and mirror is 30 cm. An upright object AB of height 1.2 cm is placed on the optic axis PQ of the lens at a distance of 20 cm from the lens.
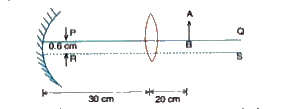
If `A^(1) B^(1)` is the image after refraction from the lens and the reflection from the mirror, find the distance of `A^(1) B^(1)` from the pole of the mirror and obtain its magnification. (b) How much part of image `A^(1) B^(1)` is above RS.
View SolutionMagnification by a lens of an object at distance 10 cm from it is -2. Now a second lens is placed exactly at the same position where first was kept, without changing the distance between object and lens. The magnification by this second lens is -3. (a) Now both the lenses are kept in contact at the same place. What will be the new magnification. (b) What is the focal length of the combination when both lenses are in contact?
View SolutionThe curved surface of a concave spherical mirror with a radius of curvature of 0.2 m is silvered. What is the focal power of this system? Refractive index of water is 4/3.

View SolutionA thin equiconvex lens of glass` ( mu = 1.5)` with radius of curvature 4m is placed on a horizontal plane mirror. When the space between the lens and mirror is filled with a liquid, an object held at a distance 6m vertically above the lens is found to coincide with its own image. What is the refractive index of the liquid.
View SolutionTwo thin converging lenses are placed on a common axis so that the optic centre of one of them coincides with the focus of the other. An object is placed at a distance twice the focal length from the left-hand lens. Where will its image be? What is the lateral magnification? The focal length of each lens is f.
View SolutionAn equiconvex lens of refractive index 1.5 and focal length 10 cm is held with its axis vertical and its lower surface immersed in water, the upper surface being in air. At what distance from the lens will a vertical beam of parallel rays incident on the lens be focussed? `mu. = 4//3`.
View SolutionIn the shown arrangement in a vertical plane, the lens forms a bright image of 'S' on the screen. The lens is suddenly released to fall freely under gravity at time t = 0. The image of source is again obtained on screen at time 'l'. Find t.
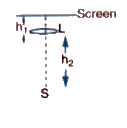
View SolutionA converging lens forms a five fold magnified image of an object. The screen is moved towards the object by a distance 0.5m, and the lens is shifted so that the image has the same size as the object. Find the lens power and the initial distance between the object and the screen.
View SolutionA plano-convex lens behaves as a concave mirror of focal length 30 cm when its plane surface is silvered and as a concave mirror of focal length 10 cm when its curved surface is silvered. What is the radius of curvature of curved surface and `mu` of the material of lens?
View SolutionA point object is placed at a distance of 20 cm on the principal axis from a thin plano-convex lens of focal length 15 cm. Find the position of final image, if the plane surface is silvered.
View SolutionFind the position of the final image formed by the lens combination given in the figure
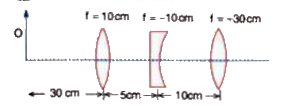
View Solution
PROBLEMS ( LEVEL-II) questions and complete solutions for chapter RAY OPTICS of JEE (MAIN AND ADVANCED) PHYSICS of Class 12