Complete Solutions to PROBLEMS (LEVEL -II) of chapter ELECTROMAGNETICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETICS |
| AAKASH SERIES | PROBLEMS (LEVEL -II) |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
Two long straight parallel wires A and B are placed 50 cm apart and carry currents 20 amp and 15 amp respectively. A point 'P' is 40 cm from wire A and 30cm from wire B. Find the magnitude of the resultant magnetic field at 'P'.
View SolutionTwo long straight conductors AOB and COD are perpendicular to each other and carry currents `I_1` and `I_2`. Find the magnitude of the magnetic inductions at a point 'P' at a distance 'a' from the point O in a direction perpendicular to the plane ACBD.
View SolutionA `2u mu C` charge moves in a circular orbit of radius 2cm around the nucleus at a frequency 10 rev/sec. Find the magnetic moment associated with the orbital motion of the particle.
View SolutionA straight wire is first bent into a circle of radius 'r' and then into a square of side 'a' each of 1 turn. If the currents flowing through them are in the ratio 2:3, find the ratio between their effective magnetic moments?
View SolutionA galvanometer of resistance `40 Omega` can measure a current of 2mA for full scale deflection. It is converted into an ammeter having range 6 times the previous value by using proper shunt. Find the resistance of ammeter so formed ?
View SolutionA solenoid 1.0 m long and 4.0 cm in diameter possesses 10 turns/cm. A current of 5.0 A is flowing through it. Calculate the magnetic induction
(a) inside and (b) at one end on the axis of solenoid.
View SolutionTwo long parallel wires are placed vertically, 10cm apart. One of them carries a current of 20A and other carries a current of 25A. Both the currents flow in the upward direction. A third wire carrying a current of 5A flowing downward is placed between the two parallel wires in such a way that its distance from the wire carrying current 20A is 6 cm. Calculate the force per unit length experienced by the third wire.
View SolutionA wire of length 5 cm is placed inside the solenoid near its centre such that it makes an angle of `30^@` with the axis of the solenoid The wire carries a current of 5A and the magnetic field due to solenoid is `2.5 xx 10^(-2)T` Calculate the force on the wire.
View SolutionA rectangular coil of area `2.0 xx 10^(-4) m^2` and 80 turns is pivoted about one of its vertical sides. The coil is in the radial horizontal magnetic field of `9.0 xx 10^(-3)` T. What is the torsional constant of the spring connected to the coil if a current of 0.1 mA produces an angular deflection of `10^@` ?
View SolutionTwo circular coils A and B of radius `(5)/(sqrt(2))` cm and 5 cm respectively carry current 5 Amp and `(S)/(sqrt(2))` AmP respectively . The plane of B is perpendicular to plane of A nd their centres coicide. Find the magnetic field at the centre.
View Solution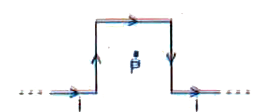
Find the magnetic field at the centre P of square of side shown in figure.
View SolutionFind the magnetic induction at the origin in the figure shown.
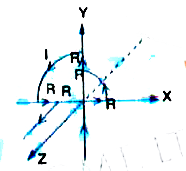
View SolutionFind the magnitude of the magnetic induction B of a magnetic field generated by a system of thin conductors, alon which a curren i is flowing at the point A (0,R,0) which is the centre of the circular conductor of radius R. The ring is yz plane.
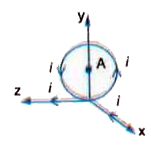
View SolutionTwo circular coils of wire each having a radius of 4cm and 10 turns have a common axis and are 6cm apart. If a current of 1 A passes through each coil in the opposite direction find the magnetic induction.
(i) At the centre of either coil ,
(ii) At a point on the axis, midway between them.
View SolutionAn electron is moving with `a^4` velocity `5 xx 10^(6) ms^(-1) hat i` in a uniform electric field of `5 xx 10^(7) Vm^(-1) j`. Find the magnitude and direction of minimum uniform magnetic field in tesla that will cause the electron to move underviated along is original path.
View SolutionA rectangular loop of wire is oriented with the left corner at the origin, one edge along X-axis and the other edge along Y-axis as shown in the figure. A magnetic field is directed into the page and has a magnitude that is given by B = `alpha` y where `alpha` is a constant. Find the total magnetic force on the loop if it carries current i.

View SolutionTwo coils each of 100 turns are held at right angles such that one lies in the vertical plane with their centres coinciding. The radius of the vertical coil is 20 cm and that of the horizontal coil is 30 cm. How would you neutralize the magnetic field of the earth at their common centre ? What is the current to be passed through each coil? Horizontal component of earth's magnetic induction`=3.49 xx 10^(-5)` T and angle of dip = `30^@`
View SolutionFind the ratio of magnetic field magnitudes at a distance 10 m along the axis and at `60^@` from the axis, from the centre of a coil of radius 1 cm, carrying a current 1 amp.
View SolutionA system of long four parallel conductors whose sections with the plane of the drawing lie at the vertices of a square carry four equal currents. The directions of these currents are as follows: those marked `ox` point away from the reader, while those marked with a dot point towards the reader. How is the vector of magnetic induction directed at the centre of the square?

View SolutionA cylindrical conductor of radius R carries a current along its length. The current density J, however, is not uniform over the cross section of the conductor but is a function of the radius according to J = br, where b is a constant. Find an expression for the magnetic field B.
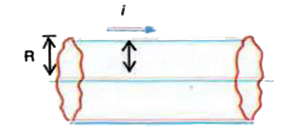
(a) at `r_1 lt R`
(b) at distance `r_2 gt R`, measured from the axis.
Hint [use Ampere's Law]
View SolutionA square current carrying loop made of thin wire and having a mass m =10g can rotate without friction with respect to the vertical axis `O O_1`, passing through the centre of the loop at right angles to two opposite sides of the loop. The loop is placed in a homogeneous magnetic field with an induction ` B = 10^(-1)T` directed at right angles to the plane of the drawing. A current I = 2A is flowing in the loop. Find the period of small oscillations that the loop performs about its position of stable equilibrium.
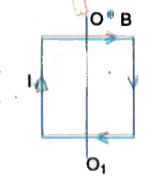
View SolutionA current i flows through an infinitely long wire having infinite bands as shown. The rad ius of the first curved section is a and the radii of the successive curved portions each increases by a factor `eta` . Find magnetic field at O.
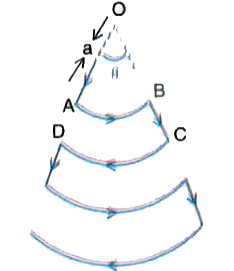
View SolutionThe diagram shows three cases. In all the three cases the circular part has radius r and straight ones are infinitely long . For the same current, i find `barB` at the centre P.

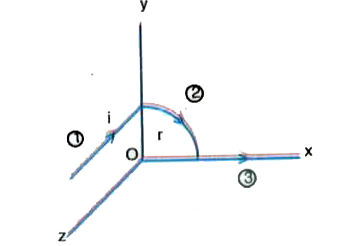
View SolutionFind magnetic field at O due to the current carrying conductor as shown in the figure.
View SolutionTwo identical particles having the same mass m and charges +q and - q separated by a distance d enter a uniform magnetic field `barB` as shown in the figure. For what value of d the particles will not collide?
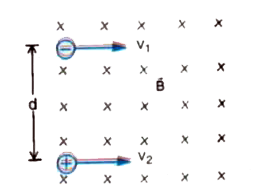
View SolutionIn the figure shown, a semi-circular wire loop of radius R is placed in a uniform magnetic field B. The plane of the loop is perpendicular to the magnetic field. Find magnetic force on the loop.
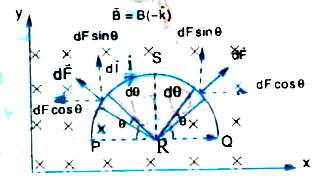
View SolutionThe flat insulating disc of radius 'a' carries an excess charge on its surface with surface charge density `sigma C//m^2`. Let the disc rotate around the axis passing through its centre and perpendicular to its plane with angular speed `omega` rad/s. If a magnetic field `vec B` is directed perpendicular to the rotation axis, then find the torque acting on the disc.
View SolutionConsider a non conducting plate of radius a and mass m which has a charge q distributed uniformly over it, The plate is rotated about its own axis with an angular speed `omega`. Show that the magnetic moment M and the angular momentum L of the plate are related as `M/L = q/(2m)`.
View SolutionA thin uniform ring of radius R carrying charge q and mass m rotates about its axis with angular velocity `omega`. Find the ratio of its magnetic moment and angular momentum.
View SolutionA wire carrying current i has the configuration as shown in figure. The two semi-infinite straight sections are both tangents to the same circle, with all sections lying in the same plane. What must `theta` in order for B to be zero at the centre of the circle?
View SolutionA uniform constant magnetic field B is directed at an angle of `45^@` to the x-axis in xy-plane. PQRS is a rigid square wire frame carrying a steady current i with its centre at the origin O. At time t=0, the frame is at rest in the position shown in the figure, with its side parallel to x and y axis. Each side of the frame is of mass M and length L.
(a) What is the torque `vec tau` about O acting on the frame due to magnetic field?
(b) Find the angle by which the frame rotates under the action of this torque in a short interval of time `Delta t`, and the axis about which this rotation occurs `(Delta t` is so short that any variation in the torque during this interval may be neglected).
View SolutionA non-conducting sphere of radius R charged uniformly with surface density `simga` rotates with an angular velocity `omega` about the axis passing through its centre. Find the magnetic induction at the centre of the sphere.
View SolutionRing of radius R having uniformly distributed charge Q is mounted on a rod suspended by two identical strings as shown in fig. The tension in strings in equilibrium is `T_0`. Now a vertical magnetic field is switched on and the ring is rotated at constant angular velocity `Omega`. Find the maximum `Omega` with which the ring can be rotated if the strings can withstand a maxiumum tension `(3T_0)/(2)`
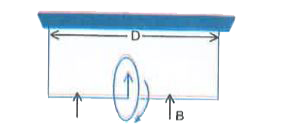
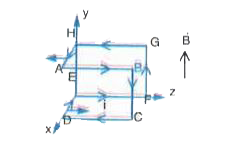
View SolutionGiven fig. shows a coil bent with all edges of length Im and carrying a current of 1A. There exists in space a uniform magnetic field of 2T in the positive y-direction. Find the torque on the loop.
View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at a distance `x_0` from the wire is projected towards it with a speed v, as shown in Fig. Find the minimum separation between the wire and the particle.
View Solution
PROBLEMS (LEVEL -II) questions and complete solutions for chapter ELECTROMAGNETICS of JEE (MAIN AND ADVANCED) PHYSICS of Class 12