Complete Solutions to PROBLEMS (LEVEL - I) of chapter WAVE MOTION AND SOUND of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE MOTION AND SOUND |
| AAKASH SERIES | PROBLEMS (LEVEL - I) |
| Number Of Questions | 60 |
| Academic Year | 2023-24 |
For the wave `y = 5 sin 30 pi [t -(x//240)]`, where x and y are in cm and t is in seconds, find the
Displacement when t = 0 and x = 2cm
View SolutionFor the wave `y = 5 sin 30 pi [t -(x//240)]`, where x and y are in cm and t is in seconds, find the
Wavelength
View SolutionFor the wave `y = 5 sin 30 pi [t -(x//240)]`, where x and y are in cm and t is in seconds, find the
Velocity of the wave.
View SolutionFor the wave `y = 5 sin 30 pi [t -(x//240)]`, where x and y are in cm and t is in seconds, find the
Frequency of the wave
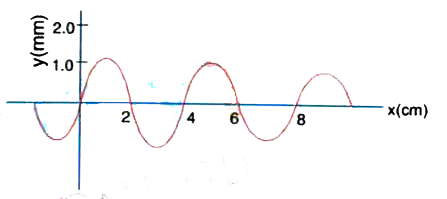
View SolutionFigure shows a plot of the transverse displacement of the particle of a string at t = 0 through which a travelling wave is passing in the positive x-direction. The wave speed is 20 cm/s. Find (a) the amplitude, (b) the wavelength, (c) the wave number and (d) the frequency of the wave.
View SolutionA wave of frequency 500 Hz has a wave velocity of 350 m/s.
Find the distance between two points which are `60^@` out of phase.
View SolutionA wave of frequency 500 Hz has a wave velocity of 350 m/s.
Find the phase difference between two displacements at a certain point at times `10^(-3)`s apart.
View SolutionA sound wave of frequency 100 Hz is travelling in air. The speed of sound in air is 350 m/s.
By how much is the phase changed at a given point in 2.5 ms?
View SolutionA sound wave of frequency 100 Hz is travelling in air. The speed of sound in air is 350 m/s.
What is the phase difference at a given instant between two points separated by a distance of 10.0 cm along the direction of propagation?
View SolutionA progressive wave of frequency 500 Hz is travelling with a speed of 350 m/s. A compressional maximum appears at a place at a given instant. The minimum time interval after which of refraction maximum occurs at the same place is
View SolutionCalculate the speed of a transverse wave in a wire of `1.0 mm^2` cross-section under a tension of 0.98 N. Density of the material of wire is `9.8 xx 10^3 kg//m^3`.
View SolutionTwo wires of different densities but same area of cross-section are soldered together at one end and are stretched to a tension T. The velocity of a transverse wave in the first wire is double of that in the second wire. Find the ratio of the density of the first wire to that of the second wire.
View SolutionA 4 kg block is suspended from the ceiling of an elevator through a string having a linear mass density of `19.2 xx 10^(-3) kg m^(-1)`. Find the speed with which a wave pulse can travel on the string if the elevator accelerates up at `2ms^(-2)(g=10 ms^(-2))`
View SolutionTransverse waves are generated in two uniform wires A and B of the same material by attaching their free ends to a vibrating source of frequency 200 Hz. The Area of cross section of A is half that of B while tension on A is twice than on B. The ratio of wavelengths of the transverse waves in A and B is
View SolutionTwo progressive transverse waves given by `y_(1) =0.007 sinpi ( 12x- 500 t )`and `y _(2) = 0.07 sin pi ( 12x+500t)` travelling along a stretched string from nodes and antinodes . What is the displacement at the (a) nodes (b) antinodes ? What is the wavelength of the standing wave ?
View SolutionTwo progressive transverse waves given by `y_(1) =0.007 sinpi ( 12x- 500 t )`and `y _(2) = 0.07 sin pi ( 12x+500t)` travelling along a stretched string from nodes and antinodes . What is the displacement at the (a) nodes (b) antinodes ? What is the wavelength of the standing wave ?
View SolutionTwo progressive transverse waves given by `y_(1) =0.007 sinpi ( 12x- 500 t )`and `y _(2) = 0.07 sin pi ( 12x+500t)` travelling along a stretched string from nodes and antinodes . What is the displacement at the (a) nodes (b) antinodes ? What is the wavelength of the standing wave ?
View SolutionA wave of length 2m is superposed on its reflected wave to form a stationary wave. A node is located at x = 3m. The next node will be located at x=
View SolutionThe Equation for the vibration of a string fixed at both ends vibrating in its third harmonic is given by `y = 2 sin (0.6x) cos (500 pi t)` (x, y are in cm t is in sec). The length of the string is
View SolutionTwo wires are kept tight between the same pair of supports. The tensions in the wires are in the ratio 2:1, the radii are in the ratio 3:1 and the densities are in the ratio 1:2. Find the ratio of their fundamental frequencies.
View SolutionA one metre long streched string having a mass of 40 g is attached to a tuning fork. The fork vibrates at 128 Hz in a direction perpendicular to the string. What should be the tension in the string if it is to vibrate in four loops?
View SolutionA streched wire resonates with a given tuning fork forming standing waves with five antinodes between the two bridges when a mass of 9 Kg is suspended from the wire. When this mass is replaced by a mass 'M' the wire resonates with the same tuning fork for three antinodes for the same positions of the bridges the value of M is
View SolutionA guitar string is 90 cm long and has a fundamental frequency of 124 Hz. Where should it be pressed to produce a fundamental frequency of 186 Hz?
View SolutionThe frequency of a sonometer wire is 100Hz. When the weights producing the tensions are completely immersed in water the frequency becomes 80Hz and on immersing the weights in a certain liquid the frequency becomes 60Hz. Find the specific gravity of the liquid
View SolutionWhen the tension in a string is increased by 44%. the frequency increased by 10Hz the frequency of the string is
View SolutionA steel wire of length im, mass 0.1kg and uniform cross sectional area `10^(-6) m^(2)` is rigidly fixed at both ends. The temperature of the wire is lowered by `20^(@)C`. If the transverse waves are set up plucking the string in the middle, calculate the frequency of the fundamental mode of vibration. `(Y=2xx10^(11)N//m^(2), a=1.21xx10^(-5)//^(@)C)`
View SolutionA metallic wire with tension T and at temperature `30 ^0 C` vibrates with its fundamental frequency of 1 kHz. The same wire with the same tension but at `10 ^0 C` temperature vibrates with a fundamental frequency of 1.001 kHz. The coefficient of linear expansion of the wire is
View SolutionThree resonant frequencies of a string are 90, 150 and 210 Hz.
Find the highest possible fundamental frequency of vibration of this string.
View SolutionThree resonant frequencies of a string are 90, 150 and 210 Hz.
Which harmonics of the fundamental are the given frequencies?
View SolutionThree resonant frequencies of a string are 90, 150 and 210 Hz.
Which overtones are these frequencies?
View SolutionThree resonant frequencies of a string are 90, 150 and 210 Hz.
If the length of the string is 80 cm, what would be the speed of a transverse wave on this string?
View SolutionThe equation of a travelling sound wave is `y = 6.0 sin (600 t - 1.8 x)` where is measured in `10^(-5)` m, t in second and x in metre.
Find the ratio of the displacement amplitude of the particles to the wavelength of the wave.
View SolutionThe equation of a travelling sound wave is `y = 6.0 sin (600 t - 1.8 x)` where is measured in `10^(-5)` m, t in second and x in metre.
Find the ratio of the velocity amplitude of the particles to the wave speed.
View SolutionThe height of a cloud above the earth is 100 m. If an observer hears the sound of thunder 0.3 s after the lightening is seen what is the velocity of sound on that day?
View SolutionIn a liquid with density `900 kg//m^3`, longitudinal waves with frequency 250 Hz are found to have wavelength 8.0 m. Calculate the bulk modulus of the liquid.
View SolutionThe speed of sound as measured by a student in the laboratory on a winter day is 340 m/s when the room temperature is `17^0C`. What speed will be measured by another student repeating the experiment on a day when the room temperature is `32^0C` ?
View SolutionThe temperature at which the speed of sound in air becomes double of its value at `0^(@)C`
View SolutionThe ratio of densities of nitrogen and oxygen is 14 : 16. Find the temperature at which the speed of sound in nitrogen will be same as that in oxygen at `55^@C` ?
View SolutionAn organ pipe has two successive harmonics withb frequencies 400 and 560 Hz. The speed of sound in air is 344 m/s.
Is this an open or a closed pipe?
View SolutionAn organ pipe has two successive harmonics withb frequencies 400 and 560 Hz. The speed of sound in air is 344 m/s.
What two harmonics are these?
View SolutionAn organ pipe has two successive harmonics withb frequencies 400 and 560 Hz. The speed of sound in air is 344 m/s.
What is the length of the pipe?
View SolutionThe fundamental frequency of a closed organ pipe is 220 Hz.
Find the length of this pipe.
View SolutionThe fundamental frequency of a closed organ pipe is 220 Hz.
The second overtone of this pipe has the same wavelength as the third harmonic of an open pipe. Find the length of this open pipe. Take speed of sound in air 345 m/s.
View SolutionA source of frequency 10 kHz when vibrated over the mouth of a closed organ pipe is in unison at 300K. Find the beats produced when temperature rises by 1K
View SolutionA closed pipe and an open pipe of same length produce 2 beats, when they are set into vibration simultaneously in their fundamental mode. If the length of the open pipe is halved, and that of closed pipe is doubled, and if they are vibrating in the fundamental mode, then the number of beats produced is
View SolutionA tuning fork produces 4 beats per second with the other tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and the beat frequency is found to increase to 6 per second. What was the original frequency of the tuning fork?
View SolutionTwo tuning forks when sounded together produce 5 beats in 2 seconds. The time interval between two successive maximum intensities of sound is
View SolutionTwo progressive waves `y_(1) = 4 sin 400 pi t and y_(2) = 3 Sin 404 pi t` moving in the same direction superpose on each other producing beats. Then the number of beats per second and the ratio of maximum to minimum intensity of the resultant waves are respectively
View SolutionCalculate the frequency of beats produced in air when two sources of sound are activated, one emitting a wavelength of 32 cm and the other of 32.2cm. The speed of sound in air is 350 m/s.
View SolutionTwo sitar string A and B playing the note 'Ga' are slightly out of tune and produce betas of frequency 6 Hz.The tension in the string A is slightly reduced and the beat frequency is found to reduceto 3Hz.If the origianl frequency of Ais 324 Hz. What is the frequency of B ?
View SolutionThe frequency of a tuning fork 'A' is 2% greater than that of a standard fork 'K'. The frequency of another tuning fork 'B'is 3% less than ‘K'. When 'A' and 'B' are vibrated together 6 beats per second are heard per second. Find the frequencies 'A' and 'B'.
View SolutionA man standing at some distance from a cliff hears the echo of sound after 2s. He walks 495 m away from the cliff. He produces a sound there and recieves the echo after 5s. What is the speed of sound?
View SolutionA motor car approaching a cliff with a velocity of 90 kmph sounds the horn and the echo is heard after 20 seconds. Assuming the velocity of sound in air to be 332 ms, calculate the distance between the car and the cliff when the horn is sounded.
View SolutionA person standing between two parallel hills fires a gun. He hears the first echo after 3/2 sec, and a second echo after 5/2 sec. If speed of sound is 332 m/s, calculate the distance between the hills. When will he hear the third, fourth, fifth and sixth echo?
View SolutionA tuning fork of unknown frequency makes 5 beats per second with another tuning fork which can cause a closed organ pipe of length 40 cm to vibrate in its fundamental mode. The beat frequency decreases when the first tuning fork is slightly loaded with wax, Find its original frequency. The speed of sound in air is 320 m/s.
View SolutionA traffic policeman standing on a road sounds a whistle emitting the main frequency of 2.00 kHz. What could be the appparent frequency heard by a scooter-driver approaching the policeman at a speed of 36.0 km/h? Speed of sound in air = 340 m/s.
View SolutionA person riding a car moving at 72 km/h sounds a whistle emitting a wave frequency 1250 Hz. What frequency will be heard by another person standing on the road in front of the car.
View SolutionA person riding a car moving at 72 km/h sounds a whistle emitting a wave frequency 1250 Hz. What frequency will be heard by another person standing on the road behind the car? Speed of sound in air =340 m/s.
View SolutionA car moving at 108 km/h finds another car in front of it going in the same direction at 72 km/h. The first car sounds a horn that has a dominant frequency of 800 Hz. What will be the apparent frequency heard by the driver in the front car? Speed of sound in air = 330 m/s.
View SolutionA tuning fork of frequency 328 Hz is moved towards a wall at a speed of `2 ms^(-1)`. An observer standing on the same side as the fork hears two sounds, one directly from the fork and the other reflected from the wall. How many beats per second can be heard ? (Velocity of sound in air 330 ms)
View Solution
PROBLEMS (LEVEL - I) questions and complete solutions for chapter WAVE MOTION AND SOUND of JEE (MAIN AND ADVANCED) PHYSICS of Class 12