Complete Solutions to Example of chapter ELECTRIC FIELD AND POTENTIAL of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC FIELD AND POTENTIAL |
| AAKASH SERIES | Example |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
Two charges `4muC and 1 muC` are placed at distance of 10 cm. Where should a third charge be placed between them so that it does not experience any force .
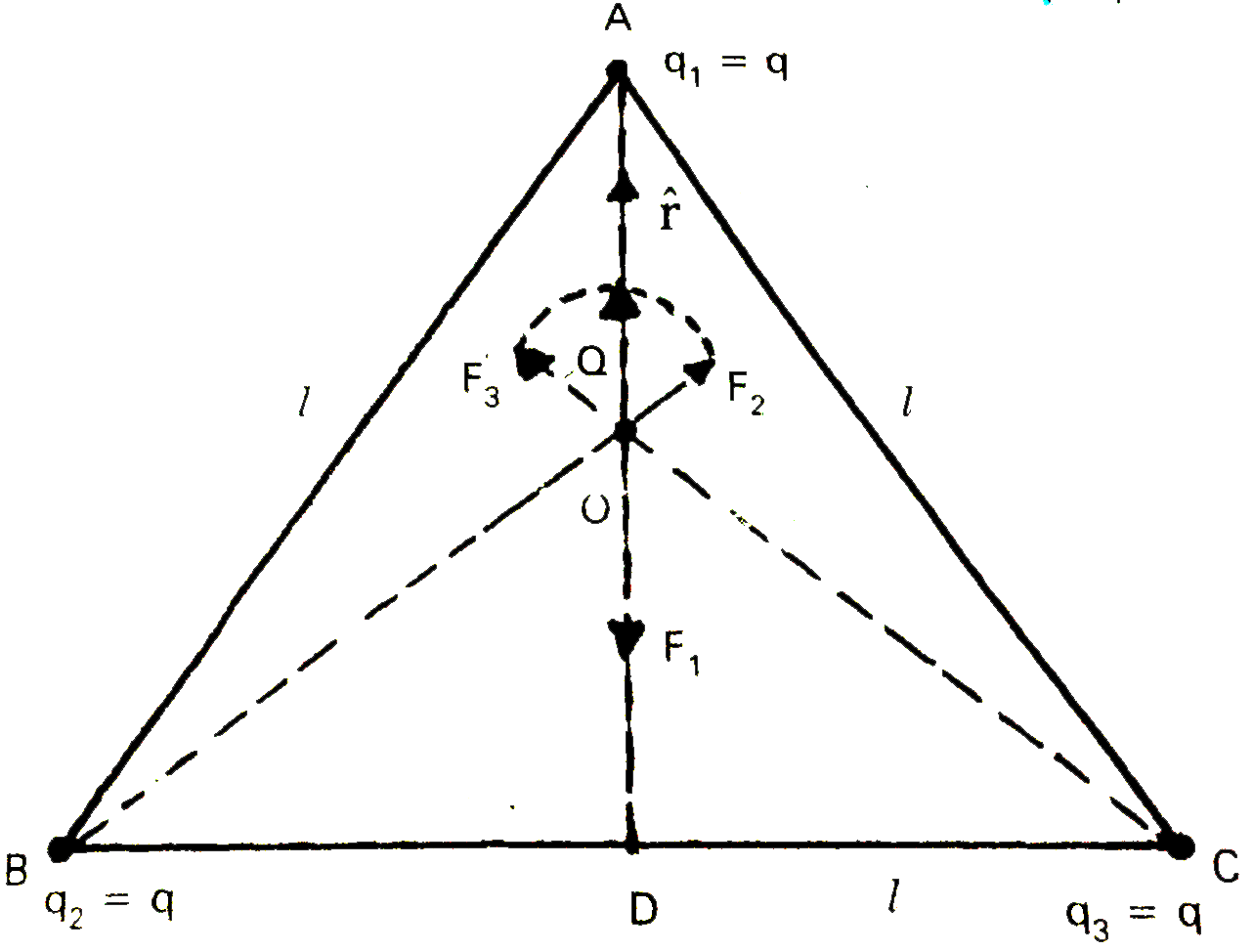
View SolutionConsider three charges `q_(1), q_(2), q_(3)` each equal to q at the vertices of an equilateral triangle of side l. What is the force on a charge Q (with the same sign as q) placed at the centroid of the triangle, as shown in Fig. ?
View SolutionCalculate the ratio of electric and gravitational force between two protons. Charge of each proton is `1.6 xx 10^(-19)C`, mass is `1.672 xx 10^(-27)kg and G= 6.67 xx 10^(-11) Nm^(2) kg^(-2)`.
View SolutionFour charges of +q, +q, +q and +q are placed at the corners A, B, C and D of a square. Find the resultant force on the charge at D.
View SolutionA charge Q is to be divided into two small objects. What should be the value of the charges on the objects so that the force between the objects will be maximum.
View SolutionTo small equally charged spheres each of mass m are suspended from the same point by silk threads of length L. The distance between the spheres `x lt lt L`. Find the rate `(dq)/(dt)` with which he charges leak off each sphere if their approach velocity varies as `vartheta =(a)/(sqrt(x))` where a si a constant.
View SolutionTwo point charges are seperated by a distance r such that a medium of dielectric constant K is occupied by a length x Now find the coulomb force between those stationary charges.
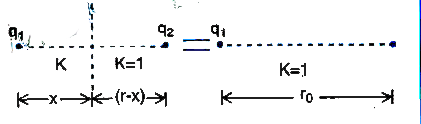
View SolutionTwo point charges `+q_(1) and +q_(2)` are located at two points with position vectors `vecr_(1) and vecr_(2)`. Find a negative charge `q_(3)` and the position vector `vecr_(3)` of the point at which it has to be placed for the force acting on each of the three charges to be equal to zero.
View SolutionA ring of radius R is with uniformly distributed charge Q on it. A charge q is now placed at the centre of the ring. Find the increment in tension in the ring.
View SolutionCharge `q_(1)` is fixed and another point charge `q_(2)` is placed at a distance `r_(0)` from `q_(1)` on a frictionless horizontal surface. Find the velocity of `q_(2)` as a function of seperation r between them (treat as point charges and mass of `q_(2)` is m)
View SolutionAn infinite number of charges each of value Q are palced on the x-axis at distances of 1, 2, 4, 8, ….. meter from the origin. If the charges are alternately positive and negative find the electric field (Intensity of electric field) at origin.
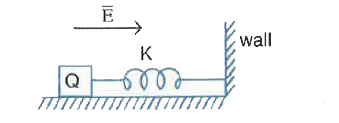
View SolutionA point mass m and charge Q is connected with a spring of negligible mass. Initially spring is in its natural length L. Now a horizontal uniform field E is switched on as shown. Find
(a) the maximum seperation between the mass and the wall
(b) Find the seperation of the point mass and wall at the equilibrium position of mass
(c ) Find the energy stored in the spring at the equi librium position of the point mass.
View SolutionA point charge `50muC` is located at a point `2 hati+3hatj`. Find the electric field vector `barE` at a point with position vector `8hati-5hatj` , when the position vectors are expressed in metre.
View SolutionA charge Q is placed at the centre of the line joining two charges q and q. The system of three charges to be in equilibrium, what should be the value of Q?
View SolutionTwo point charges `q_(1) and q_(2)` (like) are seperated by a distance r and fixed. Locate the point on the line joining those charges where resultant or net field is zero.
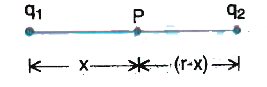
View SolutionThree charges 'q' each are vertices of an equilateral triangle of side 'r'. How much charge should be placed at the centroid so that the system remains in equilibrium.
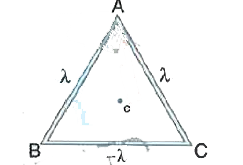
View SolutionGiven an equilateral triangle with side L, find E at its centroid. The linear charge density is as shown in figure.
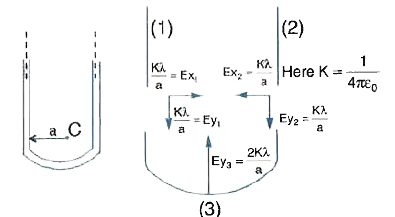
View SolutionFind the electric field at point C of the given U shaped wire which is uniformly charged with linear charge density `lambda`. [C is the centre of the semi circular section]
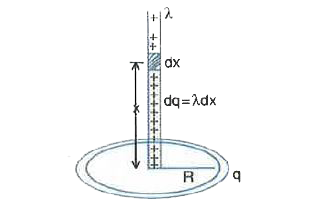
View SolutionA system consists of a him charged wire ring of radius R and a very uniformly charged thread oriented along the axis of the ring with one of its ends coinciding with the centre of the ring. The total charge of the ring is equal to q. The charge of the thread (per unit length) is equal to `lambda`. Find the interaction force between the ring and the thread.
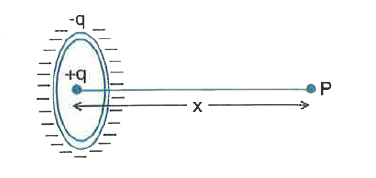
View SolutionA point charge q is located at the centre of a thin ring of radius R with uniformly distributed charge "-q". Find the magnitude of the electric field strength vector at the point lying on the axis of the ring at a distance x from its centre if `x gt gt R`.
View SolutionThere is an infinite straight chain of alternating charges q and -q. The distance between neighbouring charges is equal to d. Find the interaction energy of each charge with all the other charges.
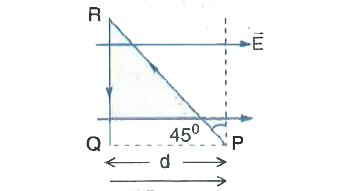
View SolutionA test charge `q_(0)` is moved without acceleration from P to Q in a uniform electric field over the path shown in figure. The points P and Q are seperated by a distance d. Find the potential difference between P and Q.
View SolutionA charge `+q_(0)` is fixed at a position in space. From a large distance another chaged particle of charge -q and mass m is thrown towards `+q_(0)` with an impact parameter L as shown. The initial speed of the projected particle is v. Find the distance of closet approach of the two particles.

View SolutionDetermine the electric field strength vector if the potential of this field depends on (x, y, z) co-ordinates as `V=A(x^(2)-y^(2))`.
View SolutionA charge `q_(0)` is moved from point P to point q along the arc PQ with centre at O as shown in the figure near a long charged wire. The linear charge density of the wire is `lambda` and it in the same plane. Find the work done in the process.

View SolutionA point charge q is isolated at the centre O of a spherical uncharged conducting layer provided with a small orifice. The inside and outside radii of the layer are equal to `r_(1) and r_(2)` respectively. Find the amount of work done to slowly transfer the charge q from the centre O, through the orifice and to infinity.
View SolutionFind the potential difference between point A and B in an electric field `barE=(2hati+3hatj+4hatk)NC^(-1)` where `barr_(A)=(hati+2hatj+hatk)m and barr_(B)=(2hati+hatj-2hatk)m`.
View SolutionAn electric field is described by the field lines as shown. Explain about the nature of the field.

View SolutionA conducting spherical bubble of radius r and thick-ness `t(t lt lt r)` is charged to a potential V. Now it collapses to form a spherical droplet. Find the potential of the droplet.
View SolutionThere is an electric field along x-direction magnitude of that electric field increases uniformly along the positive X-direction, at the rat of `10^(4)NC^(-1)` per metre. Find the force and torque experimenced by a system having a total dipole moment equal to `10^(-6)` cm in the negative X-direction.
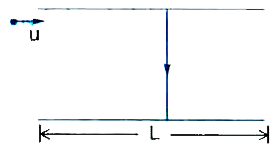
View SolutionA particle of mass m and change q enter the region between two charged plates. The length of the plate is L and there is a uniform electric field 'E' between those plates as shown. Charge q enters into the field with an initial speed U as shown. Find the vertical deflection of the particle at the far edge of the plate?
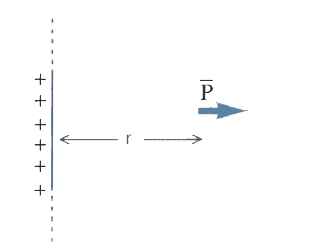
View SolutionAn electric dipole of dipole moment p is kept at a distance r from an infinite long charged wire of linear charge density `lambda` as shown. Find the force acting on the dipole.
View Solution
Example questions and complete solutions for chapter ELECTRIC FIELD AND POTENTIAL of JEE (MAIN AND ADVANCED) PHYSICS of Class 12