Complete Solutions to REVISION EXERCISE (MOVING CHANGES & MEGNETISM) of chapter APPENDICES ( REVISION EXERCISE ) of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | APPENDICES ( REVISION EXERCISE ) |
| AAKASH SERIES | REVISION EXERCISE (MOVING CHANGES & MEGNETISM) |
| Number Of Questions | 95 |
| Academic Year | 2023-24 |
A proton, a deuteron and an `alpha ` particle having same momentum enter a uniform magnetic field at right angles to the field. Then the ratio of their angular momenta during their motion in the magnetic field i
View SolutionA particle of mass 'm' and charge 'q' moves with a constant velocity 'v' along the positive x-direction. It enters a region containing a uniform magnetic field B directed along the negative Z-direction, extending from x = a to x=b. The minimum value of 'v' required, so that the particle can just enter the region x > b is
View SolutionAn electron accelerated through a potential difference 'V' passes through a uniform transverse magnetic field and experiences a force F. If the accelerating potential is increased to 2V, the electron in the same magnetic field will experience a force
View SolutionA 2 MeV proton is moving perpendicular to a uniform magnetic field of 2.5 T the force on the proton is (mass of proton = `1.6 xx 10^(-27)` kg)
View SolutionA charged particle of charge 4 mC enters a uniform magnetic field of induction `vecB = 3bari+6barj+6bark` tesla with a velocity `barv = 4bari-xbarj+y bat k`. If the particles continues to move undeviated, then the magnitude of velocity of the particle is
View SolutionAn electron beam in a TV picture tube is accelerated through a potential difference of V Volts. It passes through a region of transverse magnetic induction field (B) and follows a circular orbit of radius 'r'. The magnetic field (B) is
View SolutionWhen two electrons enter into a magnetic field with different velocities, they deflect in different circular paths, in such a way that the radius of one path is double that of the other. `1 xx 10^7 ms^(-1) ` is the velocity of the electron in smaller circle of radius `2 xx 10^(-3) m`. The velocity of electron in the other circular path is :
View SolutionA charged particle is accelerated through a potential difference of 12 kV and acquires a speed of 10 m/s. It is then injected perpendicularly into a magnetic field of strength 0.2T. Find the radius of circle described by it
View SolutionA particle of charge q and mass m is projected with kinetic energy K. into the region between two plates of uniform magnetic field of induction B as shown. If the particle is to miss collision with opposite plate the maximum value of B is

View SolutionA charged particle with velocity ` vec(upsilon) = x hati+y hatj ` moves in a magnetic field `vecB = y hati+x hatj `. Magnitude of the force acting on the particle is F. The correct option for F is a) No force will act on particle if x = y b) Force will act along y-axis if y` lt `x c) Force is proportional to `(x^2-y^2)` if x `gt` y d) Force is proportional to `(x^2 + y^2) `if y ` gt ` x
View SolutionThe radius of the dees of a cyclotron is 60cm and the magnetic field applied is 650 mT. The maximum KE of a proton accelerated through it is
`[m_p = 1.67 xx 10^(-27) kg ,q = 1.6 xx 10^(-19)C ]`
View SolutionA semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is lm, the magnetic force on the loop is
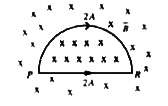
View SolutionA straight wire of length 30cm and mass 60 mg lies in a direction 30° east of north. The earth's magnetic field at this site is horizontal and has a magnitude of 0.8 G. The current must be passed through the wire so that it may float in air is `(g = 10 m//s^2)`
View SolutionA metal wire of mass 10 gm and length 10cm is placed on a smooth inclined plane of inclination 60° such that the length of wire is perpendicular of length of incline. If a current of 3A is passed through the wire vertically downward magnetic field applied for which the wire remains stationary on the inclined plane is (`g = 10m//s^2`)
View SolutionA straight horizontal wire of mass 10 mg and length 1m carries a current 2A what minimum magnetic field should be applied in the region so that the magnetic force on the wire may balance its weight
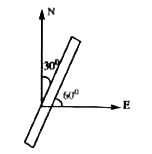
View SolutionA conductor of length 20cm and mass 18 mg lies in a direction of `60^@ ` N of E. If the horizontal component of earth's magnetic field is` 36 mu `T , the current to be passed in the conductor so that it is suspended in air is (g = 10 `ms^(-2)` )
View SolutionA parabolic section of wire, as shown in figure is located in the X-Y plane and carries a current of 12A. A uniform magnetic field B = 0.4T making an angle of 60 with X-axis exists throughout the plane. The total force acting on a wire between the origin and the point X=0.25m, y = 1.00 m.

View SolutionA thin flexible wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is
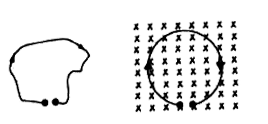
View SolutionA current I flows in an infinitely long wire with cross section in the form of a semicircular ring of radius R. The magnitude of magnetic induction along its axis is
View SolutionA current of 2A flows in a network containing two equilateral triangles of side Im as shown. The magnetic force acting on the frame is (magnetic field is 4T into the plane of paper)
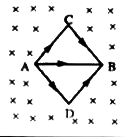
View SolutionA particle of charge `16 xx 10^(-16)` moving with velocity 10ms' along X-axis enters a region where magnetic field of induction `vecB` is along the y-axis and an electric field of magnitude `10^4 Vm^(-1)` is along the negative Z-axis. If the charged particle continues moving along X-axis, the magnitude of `vecB` is:
View SolutionA wire carrying current I is tied between points P and Q and is in the shape of a circular arch of radius R due to a uniform magnetic field B (perpendicular to the plane of the paper, shown by xxx) in the vicinity of the wore. If the wire subtends a angle `2 theta_0` at the centre of the circle (of which it forms an arch) then the tension in the wire is :
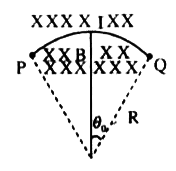
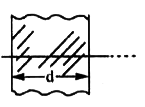
View SolutionA proton (mass m) accelerated by a potential difference V flies through a uniform transverse magnetic field B. The field occupies a region of space by width 'd'. If `alpha `' be the angle of deviation of proton from initial direction of motion (see figure), the value of sin a will be:
View SolutionA positive charge 'q' of mass 'm' is moving along the +x axis. We wish to apply a uniform magnetic field B for time `Delta `t so that the charge reverses its direction crossing the y axis at a distance d. Then :
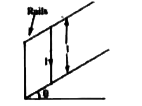
View SolutionA conducting wire of length land mass m is placed on two inclined rails as shown in figure. A current I is flowing in the wire in the direction shown. When no magnetic field is present in the region, the wire is just on the verge of sliding. When a vertically upwards magnetic field is switched on, the wire starts moving up the incline. The distance travelled by the wire as a function of time t will be:
View SolutionThe ratio of magnetic field at the centre of a circular current carrying coil to its magnetic moment is 'x'. If the current in the wire is doubled, the ratio will become (radius is constant)
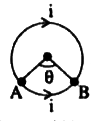
View SolutionEqual current 'i' flows in the two segments of a circular loop in the direction shown in fig. radius fo the loop is 'a'. Magnetic field at the centre of the loop is
View SolutionTwo wires A and B are of lengths 40 cm and 30 cm. A is bent into a circle of radius r and B into an arc of radius r. A current i, is passed through A and i, through B. To have the same magnetic induction at the centre, the ratio of `i_1:i_2` is
View SolutionA circular coil of radius 2R is carrying current 'i'. The ratio of magnetic fields at the centre of the coil and at a point at a distance 6R from the centre of the coil on the axis of the coil is
View SolutionThe magnetic field due to a current-carrying loop of radius 3 cm at a point on its axis at the distance of 4 cm from the centre is `54 mu T`. What will be its value at the centre of the loop?
View SolutionThe field normal to the plane of a coil of 'n' turns and radius 'r' which carries a current 'i' is measured on the axis of the coil at a small distance 'h' from the centre of the coil. This is smaller than the field at the centre by the fraction.
View SolutionThe magnetic induction at the centre of a circular coil of radius 10 cm is `5 sqrt(5)` times the magnetic induction at a point on its axis. The distance of the point from the centre of the coil, in cm is:
View SolutionA current carrying circular coil of radius 11 cm is placed with its plane in magnetic meridian. The resultant magnetic induction at the centre of the coil is (Given current in the coil is 7A and `B_(H) = 0.4 `Gauss ]
View SolutionA piece of wire carrying a current of 6A is bent in the form of a circular arc of radius 10cm and it subtends an angle of `120^@` at the centre. Find the magnetic field B due to this piece of wire at the centre.
View SolutionA particle of charge 'q' and mass 'm' moves in a circular orbit of radius 'r' with angular speed '`omega `'. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionAn electron of charge 'e' moves in a circular orbit of radius 'r' around the nucleus at a frequency 'n'. The magnetic moment associated with the orbital motion of the electron is
View SolutionTwo circular coils are made from a uniform copper wire. Radii of circular coils is in the ratio 3:4 and number of turns in the ratio 3:5. If they are connected in series across a battery
Statement (A) : Ratio between magnetic field inductions at their centers is 4:5
Statement (B): Ratio between effective magnetic moments of the two coils is 16:15
View SolutionA wire of length 1 metre is to be wound in the form of a coil have maximum magnetic moment. The suitable number of turns among the following is
View SolutionA coil of 100 turns, radius 5cm carries a current of 0.1A. It is placed in a magnetic field of 1.5T initially with its plane perpendicular to the field. The work done to rotate it through on angle of `180^@ ` is... `xx 10^(-3) 'J`
View SolutionA straight wire is first bent into a circle of radius *r' and then into a square of side 'x' each of one turn. If currents flowing through them are in the ratio 4:5, the ratio of their effective magnetic moments is
View SolutionA charge Q is uniformly distributed over the surface of nonconducting disc of the radius R. The disc rotates about an axis perpendicular to its planes and passing through its centre with an angular velocity 0. As a result of this rotation a magnetic field of induction B is obtained at the centre of the disc if we keep both the amount of charge placed on the disk and its angular velocity to be constant and varying the radius of the disc then the variation of the magnetic induction at the centre of the disc will be represented by the figure.
View SolutionTwo wires of same length are made into a circle and square respectively. Currents are passed in them such that their magnetic moments are equal. Then the ratio of the magnetic field at their respective centres (circle: square) is
View SolutionA long straight wire carrying a current of 30 A is placed in an external uniform magnetic field of induction `4xx10^(-4)` T. The magnetic field is acting parallel to the direction of current. The magnitude of the resultant magnetic induction in tesla at a point 2.0 cm away from the wire is `(mu=4pixx10^(-7)Hm^(-1))`
View SolutionTwo long parallel conductors carry currents `i_1, = 3A `and `i_2` = 3A both are directed into the plane of paper. The magnitude of resultant magnetic field at point 'P, is
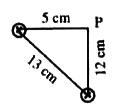
View SolutionCurrent 'i' is flowing in hexagonal coil of side a. The magnetic induction at the centre of the coil will be
View SolutionA straight wire of length `(pi^2)` meter is carrying a current of 2A and the magnetic field due to it is measured at a point distance lcm from it. If the wire is to be bent into a circle and is to carry the same current as before, the ratio of the magnetic field as its centre to that obtained in the first case would be
View SolutionA long straight wire of radius 'a' carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetic fields at a/2 and 2a is
View SolutionTwo long straight conductors AOB and COD are perpendicular to each other and carry currents `I_1 and I_2` The magnitude of the magnetic inductions at a point 'P' at a distance 'a' from the point in a direction perpendicular to the plane ACBD is
View SolutionA wire loop PQRSP is constructed by joining two semi circular coils of radii `r_1 and r_2` respectively as shown in the fig. current is flowing in the loop. The magnetic induction at point 'O' will be

View SolutionThe total magnetic induction at point 0 due to curved portion and straight portion in the following figure, will be
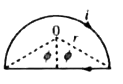
View SolutionAn infinitely long wire is bent in the form of a semicircle at the end as shown in the figure. It carries current I along abcdo. If radius of the semicircle be R, then the magnetic field at 'O' which is the centre of the circular part is
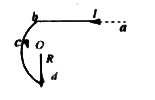
View SolutionThe magnetic induction at point 'O' in the following fig. will be
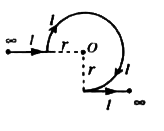
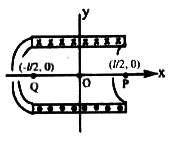
View SolutionA wire loop carrying current 'T' is placed in the x-y plane. Magnetic induction at P is
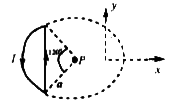
View SolutionThick and thin wires give rise to 3 different squares x,y and z as shown in figure. The magnetic field at the centre of

View SolutionIf the resistance of upper half of a rigid loop is twice that of the lower half the magnitude of magnetic induction at the centre is equal to

View SolutionAn infinitely long conductor PQR is bent to form a right angle as shown. A current I flows through PQR. The magnetic field due to this current at the point Mis B, Now another infinitely long straight conductor QS is connected to Q so that the current is 1/2 in QR as well as in QS, the current in PQ remaining unchanged. The magnetic field at M is now B. The ratio B/B, is given by
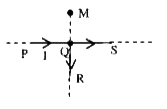
View SolutionA straight conductor of length 32 cm carries a current of 30 A. Magnetic induction at a point in air at a perpendicular distance of 12 cm from the mid-point of the conductor is
View SolutionTwo parallel long wires carry currents 18A and 3A. When the currents are in the same direction, the magnetic field at a point midway between the wire is `B_1` If the direction of` i_2` is reversed, the field becomes `B_2` Then the value of `B_1,//B_2` is
View SolutionDue to straight current carrying conductor, a null point occurred at pon east of the conductor. The net magnetic induction at a point Q which is half the distance of 'p on north of the conductor is
View SolutionA long straight wire along the z-axis carries a current 'i' in the negative z direction. The magnetic vector field `barB` at a point having coordinates (x,y) in the z = 0 plane is
View SolutionA wire carrying a current i is first bent in the form of a square of side a and placed at right angle to a uniform magnetic field of induction B. The work done in changing its shape into a circle is
View SolutionTwo mutually perpendicular conductors carry currents `i_1` and `i_2`, along X-axis and y-axis respectively. The locus of the points at which magnetic induction is zero.
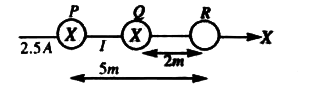
View SolutionTwo long parallel wires carrying currents 2.5A and I amp in the same direction (directed into plane) are held at P and Q respectively as shown. The points P and Q are located at 5 m and 2m respectively from a collinear point R. An electron moving with a velocity of `4 xx 10^5` m/s along positive x axis experiences a force of `3.2 xx 10^(-20)`N at the point 'R'. The value of I is
View SolutionA toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic fields, outside the toroid, inside the core of the toroid and in the empty space surrounded by the toroid are
View SolutionIn the shown figure, AC and BD are straight conductors and CED and AFB are semicircular conductors with radii r and 4r, respectively. The entire setup is lying in the same plane. If i is current entering at A what fraction of i will flow in the ACEDB such that resultant magnetic field at O is zero

View SolutionA solenoid of length 'l' has N turns of wire closely spaced, each turn carrying a current i. If R is cross sectional radius of the solenoid, the magnetic induction at 'P'(only axial component).
View SolutionA 3.0 cm wire carrying current of 10A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27T. The magnetic force on the wire is
View SolutionA closely wound solenoid of 800 turns and area of cross section `2.5 xx 10^(-4) m^2` carries a current of 3.0A. What is its associated magnetic moment?
View SolutionIf the solenoid in the above problem is free to turn about the vertical direction and a uniform horizontal magnetic field of 0.25T is applied, what is the magnitude of torque on the solenoid when its axis makes an angle of 30' with the direction of applied field?
View SolutionA solenoid of 1000 turns is wound uniform on a glass tube of 50cm long and 10 cm in diameter. Find the strength of magnetic field at the centre of solenoid when 0.1 amp current is flowing through it
View SolutionA solenoid of length T has N turns of wire closely spaced, each turn carrying a current i. If R is cross sectional radius of the solenoid, the magnetic induction at 'O' is.
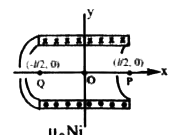
View SolutionA closely wound solenoid of 2000 turns and area of cross-section `1.6 xx 10^(-4) m^2`, carrying a current of 4.0 A, is suspended through its centre allowing it to turn in a horizontal plane. (a) What is the magnetic moment associated with the solenoid ? (b) What is the force and torque on the solenoid if a uniform horizontal magnetic field of `7.5 xx 10^(-21) T` is set up at an angle of `30^@ ` with the axis of the solenoid ?
View SolutionA Rowland ring of mean radius 15 cm has 3500 turns of wire wound on a ferromagnetic core of relative permeability 800. What is the magnetic field B in the core for a magnetizing current of 1.2A ?
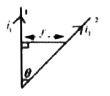
View SolutionWires 1 and 2 carrying currents i, and i, respectively are inclined at an angle `theta ` to each other. What is the force on a small element dl of wire 2 at a distancer from wire 1 due to magnetic filed of wire 1 ?
View SolutionThrough two parallel wires A and B, 10 and 2 ampere of currents are passed respectively in opposite direction. If the wire A is infinitely long and the length of the wire Bis 2m, the force on the conductor B, which is situated at 10cm distance from A will be
View SolutionThree long straight and parallel wires carrying currents are arranged as shown in fig. The wire 'B' which carries a current of 6A is placed so that it experiences no force. The distance of wire 'B' from A is then
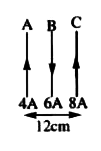
View SolutionTwo parallel horizontal conductors are suspended by light vertical threads each of length 75cm. Each conductor has a mass of 0.4 gm per m. When no current flows through them, they are 0.5 cm apart. When same current flows through each conductor the separation is 1.5 cm. The value and direction of current is
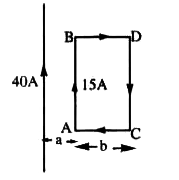
View SolutionAlong wire carrying a current of 40A as shown in figure. The rectangular loop carries a current of 15A. The resultant force acting on the loop is assume that a = 1cm, b = 80cm and 1 = 30cm ]
View SolutionTwo long parallel wires are at a distance 2d apart. They carry steady equal currents flowing out of the plane of the paper as shown. The variation of the magnetic field B along the line XX' is given by
View SolutionA conducting ring of mass 2kg, radius 0.5m carries a current of 4A. It is placed on a smooth horizontal surface. When a horizontal magnetic field of 10 T parallel to the diameter of the ring is applied, the initial acceleration is (in rad/`sec^2`)
View SolutionA wire of length 'l' is bent to form a circular coil of some turns. A current i then established in the coil and it is placed in a uniform magnetic field B. The maximum torque that acts on the coil is
View SolutionA rectangular coil 6 cm long and 2 cm wide is placed in a magnetic field of 0.02 T. If the loop contains 200 turns and carries a current of 50 mA, the torque on the coil (with loop face parallel to the field) is
View SolutionA coil carries a current and experience a torque due to a magnetic field. The value of the torque is 80% of the maximum possible torque. The angle between the magnetic field and the normal to the plane of the coil is
View SolutionA moving coil Galvanometer 'A' has 100 turns & resistance 502. Another M.C.G. 'B' has number of turns 500 and resistance `200 Omega `other quantities are same in both cases. They are connected by a battery of `50 Omega `. The ratio of deflection of B to A is
View SolutionA tangent galvanometer has coil of 50 turns and mean diameter of 22cm. The current through it when the needle is deflected through `60^@` at a place where horizontal component of earth is` B_H = 30 mu T ` is
View SolutionThe shunt resistance is `(3//8)^(th)` of that of the galvanometer, then fraction of the main current that passes through the galvanometer is
View SolutionA galvanometer having a resistance of `50Omega` , gives a full scale deflection for a current if `0.05` A. The length in metre if a resistance wire of area of cross- section `2.97 xx10^-2cm^2` that can be used to convert the gaivanometer into an ammeter which can read a maximum of 5 A current is (specific resistance of the wire =`5xx10^-7Omega-m`)
View SolutionA galvanometer has resistance G and Current `I_g` produces full scale deflection. `S_1` is the value of the shunt which converts it into an ammeter of range 0 - 1 and `S_2` is the value of shunt for the range 0 - 21. The ratio of `S_1` and `S_2` is
View SolutionThe deflection of a galvanometer falls to 1/10th when a resistance of `5 Omega ` is connected in parallel with it. If an additional resistance of 2`Omega ` is connected in parallel to the galvanometer, the deflection is
View SolutionA moving coil galvanometer has 150 equal divisions. Its current sensitivity is 10 divisions per milli ampere and voltage sensitivity is 2 divisions per millivolt. In order that each division reads 1 volt, the resistance in ohms needed to be connected in series with the coil will be
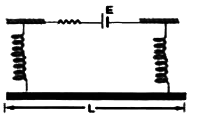
View SolutionA straight rod of mass m and length L is suspended from the identical springs as shown in Fig. The spring is stretched by distance `x_0` due to the weight of the wire. The circuit has total resistance `R_0` When a magnetic field perpendicular to the plane of paper is switched on the spring are observed to extend further by the same distance. The strength of the magnetic field applied is
View SolutionA rigid circular loop of radius r and mass m lies in the XY plane on a flat table and has a current I flowering in it. At this particular place, the earth's magnetic field is `vecB = B_x hati + B_z hatk `. The value of I so that one end of the loop lifts from the table is
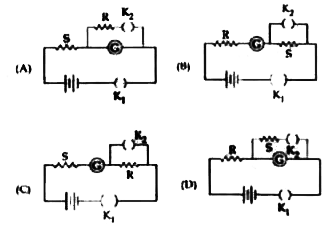
View SolutionIn the circuit diagrams (A,B,C and D) shown below, R is a high resistance and S is a resistance of the order of galvanometer resistance G. The correct circuit, corresponding to the half deflection method for finding the resistance and figure of merit of the galvanometer, is the circuit labeled as:
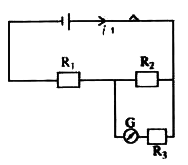
View SolutionTo find the resistance of a galvanometer by the half deflection method the following circuit is used with resistances `R_1 =9970 Omega , R_2 = 30 Omega and R_3 = 0`. The deflection in the galvanometer is d. With `R_3, =107 Omega ` the deflection changed to `(d) /(2)` the galvanometer resistance is approximately:
View SolutionA shunt of resistance `1 Omega ` is connected across a galvanometer of `120 Omega ` resistance. A current of 5.5 ampere gives full scale deflection in the galvanometer. The current that will give full scale deflection in the absence of the shunt is nearly :
View Solution
REVISION EXERCISE (MOVING CHANGES & MEGNETISM) questions and complete solutions for chapter APPENDICES ( REVISION EXERCISE ) of JEE (MAIN AND ADVANCED) PHYSICS of Class 12