Complete Solutions to Practice Exercise of chapter HYPERBOLA of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | HYPERBOLA |
| AAKASH SERIES | Practice Exercise |
| Number Of Questions | 55 |
| Academic Year | 2023-24 |
Equation of the hyperbola with foci (+-2 ,0) and eccentricity 3/2 is
View SolutionEquation of the hyperbola of eccentricity 3 and the distance between whose foci is 24 is
View SolutionThe equation of the hyperola with its transverse axis is parallel el to x-axis and its centre (3,-2) the length of axes are 8,6 is
View SolutionThe equation of the hyperola whose centre is (5,2) vertex is (9,2) and the length of conjugate axis is 6 is
View SolutionThe equation of the hyperola whose vertices are (2,5), (2,-1) and eccentricity 4/3 is
View SolutionThe equation to hyperola whose centre is (0,0) distance between the foci is 18 and distance between the directrices is 8 is
View SolutionEquation of the hyperbola with latus rectum `(22)/(5)` and eccentricity 6/5 is
View SolutionThe equation of the hyperola of given transverse axis 2a with its vertex mid-way between the centre and the corresponding focus is
View SolutionIf e is the eccentricity, l is the semi latus-rectum and S. `S^(1)` are foci of the hyperbola `9x^(2)-16y^(2)+72x-32y=16` then ascending order of l, e `SS^(1)` is
View SolutionMatch the numerical difference of the focal distance of any point on the hyperbolas
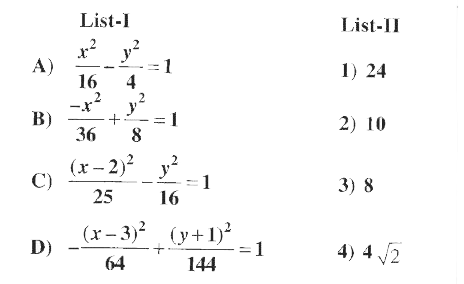
The correct Match is
View SolutionAssertion (A): The locus of the point `((e^(2t)+e^(-2t))/(2), (e^(2t)-e^(-2t))/(2))` when 't' is a parameter represents a rectangular hyperbola.
Reason (R ) : The eccentricity of a rectangular hyperbola is 2.
View SolutionIf `x^(2)/(12-k) -(y^(2))/(k-8)=1` represents a hyperbola then
View SolutionThe vertices of the hyperbola ` ((x-2)^(2))/( 9) -((y-3)^(2))/( 4) =1` are
View SolutionThe equation of the latusrecta of the hyperola `((x-4)^(2))/(16)-((y-3)^(2))/(20)=1` are
View SolutionThe length of the conjugate axis of the hyperbola ` 9x^(2) -16y^(2) - 18x -64y + 89 =0` is
View SolutionThe length of the latus rectum of the hyperbola `25x^(2)-16y^(2)=400` is
View SolutionThe foci of the hyperbola ` 9x^(2) -16y ^(2)+18x +32 y- 151=0 ` are
View SolutionThe length of the latus rectum of the hyperbola ` 9x^(2) -16y^(2) +72x -32y- 16 =0 ` is
View SolutionThe equation of directrices of the hyperbola ` 5x^(2) -4y^(2) -30x -8y -39 =0` are
View SolutionThe equations of the latus recta of the hyperbola ` 9x^(2) -16y^(2) -18x -32y -151 =0` are
View SolutionIf sec `theta` is the eccentricity of a hyper bola then the eccentricity of the conjugate hyperbola is
View SolutionThe eccentricity of the hyperbola ` 9x^(2) -16y^(2) =144 ` is
View SolutionIf the latusrectum subtends a right angle at the centre of the hyperbola then its eccentricity
View SolutionThe eccentricity of the hyperola whose latus rectum subtends a right angle at centre is
View Solutionz=x+iy is a conplex number. If the imaginary part of `z^(2)` is 32. then Locus of z is a hyperola of eccentricity.
View SolutionIn the line ` 3x-y= k ` is a tangent to the hyperbola ` 3x^(2) -y^(2) =3 `,then k =
View SolutionIf the line x `Cos alpha+y Sin alpha=p` touches `x^(2)/a^(2)-y^(2)/b^(2)=1` then `a^(2) Cos^(2)alpha-b^(2) Sin^(2)alpha=`
View SolutionThe equations of the tangents to the hyperbola ` 2x^(2) -3y^(2) =6 `which are perpendicular to the line ` x-2y+5` =0 are
View SolutionThe number of tangents to `x^(2)//25-y^(2)//9=1` through (5,0) is
View SolutionThe sum and product of the slopes of the tangents to the hyperbola `x^(2)/4-y^(2)/2=1` drawn from the point (3,-2) are
View SolutionThe slopes of the tangents drawn form (0,2) to the hyperbola `5x^(2)-y^(2)=5` is
View SolutionThe point of contact of 5x+6y+1=0 to the hyperbola `2x^(2)-3y^(2)=2 ` is
View SolutionThe condition that the line y=mx+c may be a tangent to `(y^(2))/(a^(2))-x^(2)/b^(2)=1` is
View SolutionThe locus of the point of intersection of two tangents to the hyperbola ` x^(2)//a^(2) -y^(2)//b^(2) = 1` which make an angle ` 90^(@)` with one another is
View SolutionThe radius of the director circle of the hyperbola `x^2//25-y^(2)//9=1` is
View SolutionThe radius of the auxiliary circle of the hyperbola `x^(2)//25-y^(2)//9=1` is
View SolutionThe equation of the normal to the hyperbola `x^(2)-4y^2=5` at (3,-1) is
View SolutionTangents to the hyperbola `x^(2)/a^(2)-y^(2)/b^(2)=1` makes angles `theta_(1), theta_(2)` with the transverse axis. If `theta_(1), theta_(2)` are complementary then the locus of the point of intersection of tangents is
View SolutionTangents are drawn to `3x^(2)-2y^(2)=6` from a point P. If the product of the slopes of the tangents is 2, then the locus of P is
View SolutionThe chords of contact al P.w.r.t. `x^(2)-y^(2)=a^2 and x^(2)+y^(2)=a^(2)` are at right angles. The locus of P is
View SolutionThe equation to the common tangent to the hyperbolas `(x^(2))/(25)-y^(2)/(9)=1 and (x^(2))/(9)-y^(2)/(25)+1=0` is
View SolutionThe point of intersection of two tangents to hyperbola `x^(2)/a^(2)-y^(2)/b^(2)=1` the product of whose slopes is `c^2?,` lies on the curve
View SolutionThe locus of the midpoints of chords of the hyperbola `3x^(2)-2y^(2)+4x-6=0` which are parallel to y= 2x is
View SolutionThe mid point of the chord x+2y+3=0 of the hyperbola `x^(2)-y^(2)=4` is
View SolutionThe equation of the tangent to the hyperola `x^(2)/9-y^(2)/4=1` at the point `theta=pi/3` is
View SolutionEquation of normal to `x^(2)-4y^(2)=5` at `theta=45^(@)` is
View SolutionThe equation of asymptotes of the hyperbola `4x^(2)-9y^(2)=36` is
View SolutionThe equation to the pair of asymptotes of the hyperola `2x^(2)-y^(2)=1` is
View SolutionShow that product of lengths of the perpendicular from any point on the hyperbola `x^(2)/(16)-y^(2)/(9)=1` to its asymptotes is `(144)/(25)`.
View SolutionThe equation of one asymptote of the hyperbola `14x^(2)+38y+20y^(2)+x-7y-91=0" is "7x+5y-3=0`. Then the other asymptote is
View SolutionThe equation of the hyperbola is xy-4x+3y=0 and its asymptotes are xy-4x+3y=k then k=
View SolutionThe equation of the hyperbola whose asymptotes are 3x+4y-2=0, 2x+y+1=0 and which passes through the point (1, 1) is
View SolutionNo part of the hyperbola `x^(2)/(a^(2))-y^(2)/b^(2)=1`. Lies between which of the following
View SolutionAssertion (A): The pair of asymtotes of `x^(2)/(10)-y^(2)/4=1` and the pair of asymptotes of `x^(2)/(10)-y^(2)/4=-1` coincide.
Reason (R) : A hyperbola and its conjugate hyperbola posses the same pair of asymptotes. The correct answer is
View SolutionA hyperbola whose transverse axis is along the major of the conic, (x^2)/3+(y^2)/4=4 and has vertices at the foci of this conic. If the eccentricity of the hyperbola is `3/2`, then which of the following points does NOT lie on it?
View Solution
Practice Exercise questions and complete solutions for chapter HYPERBOLA of JEE (MAIN AND ADVANCED) MATHEMATICS of Class 12
All Exercises from AAKASH SERIES Class 12 MATHS HYPERBOLA
- Additional Exercise
- Additional Solved Examples
- Example
- Examples
- Exercise
- Exercise -5.1 (Long Answer Questions)
- Exercise -5.1 (Short Answer Questions)
- Exercise -5.1 (Very Short Answer Questions)
- Exercise -5.2 (Short Answer Questions)
- Exercise -5.2 (Very Short Answer Questions)
- Exercise -5.3 (Short Answer Questions)
- Exercise -5.3 (Very Short Answer Questions)
- Exercise -I
- Exercise -II
- Practice Exercise
- Solved Examples