Complete Solutions to Exercise - I of chapter MEASURES OF DISPERSION (STATISTICS) of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | MEASURES OF DISPERSION (STATISTICS) |
| AAKASH SERIES | Exercise - I |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
If the average of the first n numbers in the sequence 148, 146, 144,….., is 125, then n =
View SolutionIn a data the number I is repeated I times for i=1, 2, …,n. Then the mean of the data is
View SolutionThe mean of 10 observations is 16.3. By an error one observations is registered as 32 instead of 23. Then the correct mean is
View SolutionMean of 100 items is 49. It was discovered that three items which should have been 60, 70, 80 were wrongly read as 40, 20, 50 respectively.The correct mean is
View SolutionThe mean weight of 9 items is 15. If one more items is added to the series now the mean becomes 16. The value of `10^(th)` item is
View SolutionConsider the frequency distribution of the given number

If the mean is known to be '3', then the value of f is
View SolutionMean of the numbers 1,2,3,…,n with respective weights
`1^(2) + 1, 2^(2) + 2, 3^(2) + 3,…,n^(2)+n` is
View SolutionThe mean of n items is `bar(x)`. If the first item is increased by 1, second by 2 and so on, then the new mean is
View SolutionThe number of observation in a group is 40. If the average of first 10 is 4.5 and that of the remaining 30 is 3.5, then the average of the whole group is
View SolutionMean of a set of numbers is `bar(x)`. If each number is increased by `lambda`, then the mean of new set is
View SolutionThe median of 5,19,14,6,8,9,12,13,21 is
View SolutionThe median of a set of 9 distinct observations is 20.5. If each of the largest 4 observations of the set is increased by 2, then the median of the new set
View SolutionMedian of `(x)/(5), x, (x)/(4), (x)/(2), (x)/(3)` is 8. If `x gt 0` then value of x is
View SolutionThe mean and median of 100 items are 50 and 52 respectively. The value of the largest item is 100. It was later found that it is actually 110. Then the true mean and median are
View SolutionMode of the data 3,2,5,2,3,6,6,5,3,5, 2, 5 is
View SolutionMode of the following distribution is

View SolutionIf the difference between mean and mode is 63, then difference between mean and median is
View SolutionIf the mode of the data 25,15,20,25,18,14,15,18,16,20,25,20,x,18 is 25 then x is
View SolutionA data consists of two 2's, four 4's, six 6's three 8s', and 10. Then the mode of data is
View SolutionThe average value of the median of 2,8,3,7,4,6,7 and the mode of 2,9,3,4,9,6,9 is
View SolutionGeometric mean of `2, 2^(2), 2^(3),…,2^(n)` is
View SolutionIf the Geometrical mean of x, 16, 50 is 20, then the value of x is
View SolutionThe reciprocal of the mean of the reciprocals of n observations is
View SolutionThe Harmonic mean of the numbers 2,3,4 is
View SolutionIf A.M. = 24.5, G.M. 24.375 then H.M. =
View SolutionIn problems on speed of a body, the average used is
View SolutionThe H.M. of the numbers 1/5, 1/10, 1/15, 1/20, 1/25, 1/30, 1/35 is
View SolutionA man travels at a speed of 20 Km/hr. and then returns at a speed of 30 Km/hr. His average speed of whole journey is
View SolutionThe mean deviation from the mean for the set of observation -1, 0, 4 is
View SolutionMean deviation from the mean for data 6, 7 10, 12, 13, 4, 8, 12 is
View SolutionThe mean deviation of the number 3, 4, 5, 6, 7 from median is
View SolutionIf mean deviation through median is 15 and median is 450, then coefficient of mean deviation is
View SolutionIn a moderated asymmetrical distribution S.D. is 20 then the mean deviation is
View SolutionThe mean and S.D. of 1,2,3,4,5,6 is
View SolutionFor a series the information available is `n = 10 sum x = 60, sum x^(2) = 1000`. The standard deviation is
View SolutionCoefficient of variation of a distribution is 60 and its standard deviation is 21, then its arithmetic mean is
View SolutionIf the mean of 10 observations is 50 and the sum of the squares of the deviations of the observations from the mean is 250, then the coefficient of variation of those observations is
View SolutionStandard deviation of first 'n' natural numbers is
View SolutionThe variance of the first 50 even natural numbers is
View SolutionThe median and S.D. of a distribution are 20 and 4 respetively. If eahc item is increased by 2, the new median and S.D. are
View SolutionThe standard deviation of 26, 27, 31, 32, 35 is
View SolutionThe standard deviation of a, a+d, a + 2d,….a + 2nd is
View SolutionThe variance of first 10 multiples of 3 is
View SolutionFor a group of 50 male workers, the mean and S.D. of their daily wages are Rs. 630 and Rs. 90 respectively. For a group of 40 female workers, these are Rs. 540 and Rs. 60 respectively. The S.D. of these 90 workers is
View SolutionIf standard deviation of 1,2,3,4,….,10 is `sigma` then standard deviation of 11, 12, …20 is
View SolutionThe standard deviation of a variable x is `sigma`. The standard deviation of the variable `(ax + b)/(c )` where a, b, c are constants is
View SolutionThe variance of observation `x_(1), x_(2),x_(3),…,x_(n)` is `sigma^(2)` then the variance of
`alpha x_(1), alpha x_(2), alpha x_(3),….,alpha x_(n), (alpha != 0)` is
View SolutionThe standard deviations of two sets containing 10 and 20 members are 2 and 3 respectively measured from their common means 5. The S.D. for the whole set of 30 members is
View SolutionThe standard deviation of the observations 22, 26, 28, 20, 24, 30 is
View SolutionThe mean of five observations is 4 and their variance is 5.2. If three of these observations are 1,2 and 6. Then the other two are
View SolutionWhich of the following is correct relations a symmetrical distribution is
View SolutionOne of the methods of determining mode is
View SolutionWhich of the following is correct for data -1, 0, 1,2,3,5,5,6,8,10,11
View SolutionIf m is mean of distribution, then `sum(x_(i) - m)` is equal to
View SolutionConsider the following statements :
(i) Mode can be computed from histogram.
(ii) Median is not independent of change of scale.
(iii) Variance is independence of change of origin and scale.
Which of these is/are correct :
View SolutionMatch the correct parts to make a valid statement
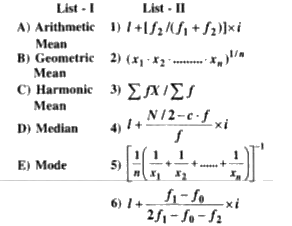
The correct match from List - I from List - II
View Solutioni. Mean = a (3 median - mode)
II. Mean - Mode = b(Mean - Median)
(iii) Median = Mode + c (Mean - mode)
View SolutionObserve the following statements :
(A) : The median of 100 items is 52. The value of the largest item is 100. It was later found that it actually 110. Therefore the true median is 52.
(R ) : The median is not effected by the extreme observations.
View SolutionTwo teams A and B have the same mean and their coefficients of variance are 4, 2 respectively. If `sigma_(A), sigma_(B)` are the standard deviations of teams A, B respectively then the relation between item is
View Solution
Exercise - I questions and complete solutions for chapter MEASURES OF DISPERSION (STATISTICS) of JEE (MAIN AND ADVANCED) MATHEMATICS of Class 12
All Exercises from AAKASH SERIES Class 12 MATHS MEASURES OF DISPERSION (STATISTICS)
- Additional Exercise (Long answer Questions)
- Additional Exercise (Short answer Questions)
- Additional Exercise (Very Short Answer Questions)
- EXAMPLE
- Exercise - 4.1 (Long answer Questions)
- Exercise - 4.1 (Very short Answer Type Questions)
- Exercise - 4.2 (Long answer Questions)
- Exercise - 4.2 (Very short Answer Questions)
- Exercise - I
- Exercise - II
- Practice Exercise
- Solved example