Complete Solutions to PRACTICE EXERCISE of chapter ELLIPSE of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | ELLIPSE |
| AAKASH SERIES | PRACTICE EXERCISE |
| Number Of Questions | 65 |
| Academic Year | 2023-24 |
If length of the major axis is 8 and e = `1/sqrt(2)`Axes are co-ordinate axes then equation of the ellipse is
View SolutionThe equation of the ellipse whose vertices are (2, 5), (2, -1) and eccentricity `sqrt(5)/(3)` is
View SolutionThe equation of the ellipse whose focus is (2, 4), centre is (3, 4) and eccentricity is 1/2 is
View SolutionThe equation of the ellipse whose centre is (5, 2) vertex is (9, 2), the length of the major axis is 8 and minor axis 6 is
View SolutionAxes are co-ordinate axes, the ellipse passes through the points where the straight line `(x)/(4)+(y)/(3)=1` meets the cood axes. Then equation of the ellipse is
View SolutionAxes are co-ordinate axes, A and B are ends of major axes and minor axis, area of `triangle`OAB is 16 sq units if e=`sqrt(3)/(2)` then equation of the ellipse is
View SolutionThe axis of the ellipse are coordinate axes. It passes through the pts P(2, 7), 2(4, 3). The equation of the ellipse is
View SolutionLatus Rectum is `4 and e=(1)/sqrt(2)` axes are coordinate axes, eq. of the ellipse
View SolutionThe equation of the ellipse with its axes as the coordinate axes and whose latus rectum is 10 and distance between the foci = minor axis is
View SolutionThe centre of a ellipse where axes is parllel to co-ordinate axes is (2, -1) and the semi axes are `sqrt(3)/(2),1/2` The equation of the ellipse is
View SolutionThe equation of the ellipse whose vertices are (-4, 1), (6, 1) and one laturs rectum is x - 4 = 0 is
View SolutionIf the equation `(x^(2))/(9-k)+(y^(2))/(5-k)=1` represents an ellipse then
View SolutionThe centre of the ellipse `4x^(2)+9y^(2)-24x+36y-72=0` is
View SolutionThe foci of the ellipse `36x^(2) + 9y^(2) = 324` are
View SolutionThe coordinates of the foci of the ellipse `4x^(2) + 9y^(2) = 1` are
View SolutionThe length of the latusrectum of `((x-3)^(2))/(16)+(y-2)^(2)/(36)=1` is
View SolutionThe equation of the minor axis of the ellipse `(x-1)^(2)/(9)+(y-6)^(2)/(4)=1` is
View SolutionThe equations of the directrices of the ellipse `9x^(2) + 25y^(2) = 225` are
View SolutionThe vertices of the ellipse `9x^(2) + 25y^(2) - 90x - 150y + 225 = 0` are
View SolutionThe foci of the ellipse `9x^(2)+ 5(y^(2)-10y +25)=45` are
View SolutionThe equation of the major axis of `25x^(2) + 16y^(2)-100x - 96y - 156 = 0` is
View SolutionThe equations of the latus recta of the ellipse `9x^(2) + 25y^(2) - 36x + 50y - 164 = 0` are
View SolutionThe equations of the directrices of `16x^(2) + 25y^(2) - 96x - 100y - 156 = 0` are
View SolutionThe asending order of the eccentricities `l_(1),l_(2),l_(3)` of the conics `12x^(2) + 3y^(2) = 15, x^(2) +2y^(2) = 6, 4(x-1)^(2) + 3(y+2)^(2) = 12`
View SolutionLet P be a point on an ellipse whose parameter is `(pi)/(3)` . The sum and differences of the focal distances of P is 8 and 3 then the eccentricity of the ellipse is
View SolutionMatch the eccentricities of the ellipses
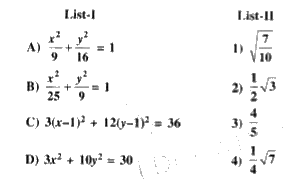
The correct Matching is
View SolutionAssertion (A) : the sum and product of the slopes of the tangents to the ellipse `(x^2)/(9)+(y^2)/(4)=1` drawn from the points (6,-2) are `-8/9`,1. Reason(R): if `m_(1),m_(2)` are the slopes of the tangents through `(x_(1),y_(1))` of the ellipse, then `m_(1)+m_(2)=(2x_(1).y_(1))/(x_(1)^(2)-a^(2))` `m_(1).m_(2)=(y_(1)^(2)-b^(2))/(x_(1)^(2)-a^(2))`
View SolutionIf the latusrectum of an ellipse is half of its major axis then e is
View SolutionIf the latus rectum of an ellipse is half of its minor axis then e =
View SolutionThe distance between the directrix is equal to 8 times the distance between the foci then e =
View SolutionIf the m inor axis of an ellipse form s an equilateral triangle with one vertex of the ellipse then e =
View SolutionLet `S, S^(')` are the focii and `BB^(')` be the minor axis of an ellipse. If `angleBSS^(')=theta` then its eccentricity is
View SolutionThe length of the latus rectum of an ellipse is 4. The focus and its corresponding directrix are (1, -2 ) and 3x + 4y - 15 = 0 then the eccentricity of the ellipse is
View SolutionLet P be a point on an ellipse whose parameter is `(pi)/(3)` . The sum and differences of the focal distances of P is 8 and 3 then the eccentricity of the ellipse is
View SolutionThe latus rectum `LL^(')` subtends a right angle at the centre of the ellipse, then its eccentricity is
View SolutionIf the latus rectum of a hyperola forms an equilateral triangle with the centre of the hyperbola, then its eccentricity is
View SolutionArea of the quadrilateral formed by the extremities of major axis and minor axis is `8sqrt(3)`. The distance between foci is `4sqrt(2)`. Then eccentricity of the ellipse is
View SolutionIf `x+ky-5=0` is a tangent to the ellipse `4x^(2)+9y^(2)=20` then k =
View SolutionThe equations of the tangents to the ellipse `3x^(2)+4y^(2)=12` which are parallel to the line `2x-y+5=0` is
View SolutionThe point of contact `4x-5y+25=0` with the ellipse `9x^(2)+25y^(2)=225` is
View SolutionThe number of tangents to `(x^(2))/(25)+(y^(2))/(9)=1` through (1,1) is
View SolutionThe product of the slopes of the tangents to the ellipse `2x^(2)+3y^(2)=6` drawn from the point (1, 2) is
View SolutionThe radius of the director circle of `16x^(2)+9y^(2)=144` is
View SolutionThe quadratic equation whose one root is `(3+sqrt(5))/(2-sqrt(5))` is
View SolutionThe equation to the auxiliary circle of `(x^(2))/(12)+(y^(2))/(18)=1` is
View SolutionThe equation of the normal to the ellipse `x^(2)/4+y^(2)/1=1` at (2, -1) is
View SolutionThe equations of the tangents drawn from (2, 3) to the ellipse `9x^(2) + 16y^(2) = 144`
View SolutionIf `a gt b` and e is the eccentricity of the ellipse then the equation of the normal at the end of the latusrectum in the first quadrant is
View SolutionIf the normal at one end of latusrectum of an ellipse `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1` passes through one end of minor axis then
View SolutionThe equation to the locus of point of intersection of lines `y-mx=sqrt(4m^(2)+3) and my+x=sqrt(4+3m^(2))` is
View SolutionThe number of tangents that can be drawn to an ellipse perpendicular to a given straight lin
View SolutionIf the chords of contact of tangents from two points to the ellipse are a right angles, then show that `(x_(1)x_(2))/(y_(1)y_(2))=-(a^(4))/(b^(4))`
View SolutionThe mid point of the chord 3x - 2y + 8 = 0 of the ellipse `3x^(2) + 4y^(2) = 24` is
View SolutionThe distance of a point on the ellipse `x^(2) + 3y^(2) = 6` from its centre is 2. Find the eccentric angle of the point.
View SolutionThe equation of the tangent at a point `theta=3pi//4` to the ellipse `x^(2)//16+y^(2)//9=1` is
View SolutionThe equation of the normal to the ellipse at the point whose eccentric angle `theta=(pi)/(6)` is
View SolutionP is a point on the ellipse `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1` S and `S^(1)` are foci A & `A^(1)` are the vertices of the ellipse then the ratio `|(SP-S^(1)P)/(SP+S^(1)P)|` is
View SolutionIf the chord joining two points whose eccentric angles are `alpha` and `beta` cut the major axis of an ellipse `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1` at a distance from the centre then `tan (alpha)/(2).tan (beta)/(2)` =
View SolutionIf `alpha` and `beta` are the eccentric angles of the ends of a focal chord of the ellipse then `cos^(2)((alpha+beta)/(2))sec^(2)((alpha-beta)/(2))`=
View SolutionThe minimum area of triangle formed by the tangent to the ellipse `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1` with the coordinate axes is
View SolutionIf a tangent to the ellipse meets major and minor axis at M and N respectively and C is the centre of the ellipse thejn `(a^(2))/(CM)^(2)+(b^(2))/(CN)^(2)`=
View SolutionThe locus of the variable point P for which the chord of contact of touch the circle `x^(2)+ y^(2) = r^(2)` is
View SolutionIf `pi+theta` is the eccentric angle of a point on the ellipse `16x^(2)+25y^(2) = 400` then the corresponding point on the auxiliary circle is
View SolutionThe locus of midpoints of chords of the ellipse `x^(2)//a^(2)+y^(2)//b^(2)=1` which pass through the positive end of the major axis is
View SolutionIf y = mx + c is a normal to the ellipse `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1` if `C=
View Solution
PRACTICE EXERCISE questions and complete solutions for chapter ELLIPSE of JEE (MAIN AND ADVANCED) MATHEMATICS of Class 12
All Exercises from AAKASH SERIES Class 12 MATHS ELLIPSE
- ADDITIONAL EXERCISE
- ADDITIONAL SOLVED EXAMPLES
- EXAMPLE
- EXERCISE 4.1 (SHORT ANSWER QUESTIONS)
- EXERCISE 4.1(LONG ANSWER QUESTIONS)
- EXERCISE 4.1(VERY SHORT ANSWER QUESTIONS)
- EXERCISE 4.2 (SHORT ANSWER QUESTIONS)
- EXERCISE 4.2(VERY SHORT ANSWER QUESTIONS)
- EXERCISE 4.3 (VERY SHORT ANSWER QUESTIONS)
- EXERCISE-I
- EXERCISE-II
- PRACTICE EXERCISE
- SOLVED EXAMPLES