Complete Solutions to Solved Example of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| AAKASH SERIES | Solved Example |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
A page is opened at random from a book containing 600 pages. What is the probability that the number on the page is a perfect square.
View SolutionFind the probability that a leap year will have 53 sundays.
View SolutionIf 4 fair coins are tossed simultaneously, then find the probability that 2 heads and 2 tails appear.
View SolutionFind the probability of throwing a total score 8 with 2 dice.
View SolutionTwo dice are rolled. What is the probability that none of the dice shows the number 2 ?
View SolutionA single die is rolled twice in succession. What is the probability that the number showing on the second toss is greater than that on the first rolling?
View SolutionIf two cards are drawn from pack 52 cards at random, then find the probability of getting both club cards.
View SolutionA and B are among 20 persons sit at random along a round table. Find the probability that there are any 6 persons between A and B.
View SolutionA class has `15` boys and 5 girls. Suppose three students are selected at random from the class. Find the probability that they are all boys.
View SolutionA box contains 20 screws of which 5 are defective. Two screws are drawn at random. Find the probability of the event that
(i) neither of the 2 screws is defective.
(ii) atleast one of them is defective.
View SolutionOut of 30 consecutive integers two are drawn at random. Then what is the probability that their sum is odd.
View SolutionSuppose `S={1,2,3,4}` is the sample space of a random experiment, Suppose `P(1)=x`, `P(2)=2x`, `P(3)=3x`, and `P(4)=4x`, where `P` is a probability function . Find x.
View SolutionIf four people are chosen at random, then the probability that no two of them were born in the same day of the week
View SolutionOut of 30 consecutive integers, three integers are drawn at random. Find the probability that their sum is (i) an odd number (ii) an even number
View SolutionIf `E_(1),E_(2)` are two events with `E_(1)capE_(2)=phi` then show that `P(E_(1)^(C)capE_(2)^(C))=P(E^(C))-P(E_(2))`
View SolutionIf `P(A)=x`, `P(B)=y` and `P(AnnB)=z`. Find `P(A^(c )nnB^(c ))`.
View SolutionTwo events A and B have the probabilities `0.25` and `0.5` respectively. The probability that both A and B occur simultaneously is `0.14`. Find the probability that neither A nor B occurs.
View SolutionThe probability of the event A occuring is 0.5 and of B occurring is `0.3`. If A and B are mutually exclusive events then the probability of neither A nor B occuring is
View SolutionFor any two events A,B shows that
`P(AcapB)-P(A)P(B)=P(A^(C))P(B)-P(A^(C)capB)`
`=P(A)P(B^(C))-P(AcapB^(C))`
View SolutionA and B are seeking admission into I.I.T. If the probability for A to be selected is 0.5 and that both to be selected is 0.3. Is it possible that the probability of B to be selected is 0.9?
View SolutionIn an experiment of drawing a card at random from a pack, the event of getting a spade is denoted by A and getting a picture card (king, Queen or jack) is denoted by B. Find the probabilities of `A,B,AcapBandAcupB.`
View SolutionIf two cards are drawn from pack 52 cards at random, then find the probability of getting both red or both kings.
View SolutionThree students A,B,C are to take part in a swimming competition. The probabilities of A's winning or the probability of B's winning is 3 times the probability of C's winning. The probability of the event of either B or C to win is
View SolutionIf `(1+3p)/(3)`, `(1-p)/(4)`, `(1-2p)/(2)` are the probabilities of 3 mutually exclusive events then find the set of all values of p.
View Solution(i) If A,B,C are any three events in an experiment and `AsubeB`, `P(C ) gt 0` then show that `P(A//C) le P(B//C)`
(ii) If A, B are mutually exclusive and `P(B) ne 1` then show that `P(A//B^(C ))=(P(A))/(1-P(B))`
(iii) If A, B are mutually exclusive and `P(AuuB) ne 0` then `P(A//AuuB)=(P(A))/(P(A)+P(B))`
View SolutionSuppose A and B are independent events with `P(A)=0.6`, `P(B)=0.7` then compute
`(i) P(AnnB)` `(ii) P(AuuB)`
`(iii) P(B//A)` `(iv) P(A^(c )nnB^(c ))`
View SolutionA pair of dice are rolled. What is the probability that neither die shows a 2, given that they sum to 7 ?
View SolutionAn urn contains 12 red balls and 12 green balls. Suppose two balls are drawn one after another without replacement . Find the probability that the second ball drawn is green given that the first ball drawn is red.
View SolutionSuppose there are 12 boys and 4 girls in a class. If we choose three children one after another in succession at random, find the probability that alll the three are boys.
View SolutionFind the probability of drawing 2 red balls in succession from a bag containing 4 red balls and 5 black balls when the ball that is drawn first is
(i) not replaced (ii) replaced
View SolutionIf A,B,C are independent events, shows that `AcupBandC` are also a independent events.
View SolutionIf A and B are two independent events, and `P(A)=1//4`, `P(B)=1//3` then find `P(A-B)uu(B-A))`. i.e., propbability of occurrence of exactly one of the events A and B.
View SolutionThe probability that A hits a target is `1//4` and the probability that B hits the target is `1//3`. If each of then fired once, what is the probability that the target will be hit atleast once ?
View SolutionIn a shooting test the probability of A,B,C hitting the targets are `(1)/(2),(2)/(3)and(3)/(4)` are respectively. If all of them first at the same target. Find the probability that
i) Only one of them hits the target,
ii) atleast one of them hits the target.
View SolutionAn urn contains 10 white balls and 5 black balls. Two players Q and R alternatively draw a ball with replacement from the urn. The player that draws a white ball first wins the game. If Q begins the game, find the probability of his winning the game.
View SolutionBag `B_(1)` contains 4 white and 2 black balls.
Bag `B_(2)` contains 3 white and 4 black balls.
A bag is drawn at random and a ball is chosen at random from it. What is the probability that the ball drawn is white.
View SolutionBag A contains 4 white and 7 black balls. Bag B contains 5 white and 6 black balls. A die is rolled . If 2 or 5 turns up then choose bag A otherwise choose bag B. If one ball is drawn at random from the selected bag, then find the probability that it is black.
View SolutionBag A contains 4 white and 3 black balls. Bag B contains 3 white and 2 black balls. One ball is transferred from bag A to bag B. Now one ball is drawn from bag B. Find the probability that it is white.
View SolutionThree boxes numbered I,II,III contain the balls as follows.
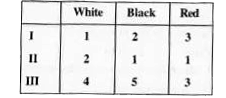
One box is randomly selected and a ball is drawn from it. If the ball is red, then find the probability that it is from box II.
View SolutionA survey shows that in a certain village 2 out of every 100 men and 1 out of every 100 women have strength ulcers. A person selected at random from the village is found to have stomach ulcer. Find the probability that the person is a male, given that the probability of selecting a male from the village is `0.55`.
View SolutionA bag contains 5 balls the colours of which are not known. Two balls are drawn and found them to be red. Find the probability that all the balls in the bag are red.
View SolutionA man is known to speack the truth 2 out of 3 times . He throws a die and reports that it is a six . The probability that it is actually a six is
View SolutionA letter is known to have come from either 'MAHARASTRA` or `MADRAS` on the post mark only consecutive letters 'RA' can be read clearly. What is the chance that the letter came from 'MAHARASTRA'.
View SolutionSuppose that an unbaised pair of dice is rolled. Let A denote the event that the same number shows on each die. Let B denote the event that the sum is greater than 7. Find (i) `P((A)/(B))` ii) `P((B)/(A))`
View SolutionProve that A and B are independent events if and only if `P((A)/(B))=P((A)/(B^(C)))`
View Solution
Solved Example questions and complete solutions for chapter PROBABILITY of JEE (MAIN AND ADVANCED) MATHEMATICS of Class 12
All Exercises from AAKASH SERIES Class 12 MATHS PROBABILITY
- Additional Exercise
- Additional Solved Example
- Example
- Exercise 2.1(short answer type question)
- Exercise 2.1(very short answer)
- Exercise 2.2(short answer type question)
- Exercise 2.2(very short answer type question)
- Exercise 2.3(long answer type question)
- Exercise 2.3(short answer type question)
- Exercise 2.3(very short answer type question)
- Exercise-I
- Exercise-II
- Practise Exercise
- Solved Example