Complete Solutions to Practice Sheet- Exercise-IV of chapter CHEMICAL THERMODYNAMICS of Class 12 book with complete answers and questions
| Class 12 | CHEMISTRY |
| Chapter | CHEMICAL THERMODYNAMICS |
| AAKASH SERIES | Practice Sheet- Exercise-IV |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
For a perfectly crystalline solid `C_(p.m) = aT^(3)`, where a is constant. If `C_(p.m)` is 0.42 J/K `-` mol at 10K, molar entropy at 10K is
View SolutionA copper block of mass 'm' at temperature `'T_(1)'` is kept in the open atmosphere at temperature `'T_(2)'` where `T_(2) gt T_(1)`. The variation of entropy of the copper block with time is best illustrated by
View SolutionThe ratio of P to V at any instant is constant and is equal to 1. for a monoatomic ideal gas under going a process. What is the molar heat capacity of the gas
View SolutionWhich of the following statements are incorrect
View SolutionA diatomic ideal gas initially at 273K is given 100cal heat due to which system did 209J work. Molar heat capcity (Cm) of gas for the process is:
View SolutionFor an ideal monoatomic gas during any process T=kV, find out the molar heat capacity of the gas during the process. (Assume vibrational degree of freedom to be active)
View SolutionHere `T_(1) and T_(2)` are
View Solution(A): Entropy of a perfect crystalline substance at absolute zero is zero
(R ): At absolute zero translation kinetic energy of a system is zero.
View SolutionWhich of the following statement is incorrect?
View SolutionThe entropy change of `x_(2)` gas, during the following irreversible process, approximately is how much? `x_(2)` gas (`27^(@)C`, 1 atm, 5 moles ) `rarr x_(2)` gas (`117^(@)C`, 5 atm, 5 moles) (`C_(P)` of `x_(2)` = 6.95 cal/mol/`""^(@)C`), log 1.3= 0.1139
View SolutionFor polytropic process `PV^(n)` = constant, `C_(m)` (molar heat capacity) of an ideal gas is given by
View Solution2 mole of an ideal mono atomic gas undergoes a reversible process for which `PV^(2)=C`. The gas is expanded from initial volume of 1L to a final volume of 3L starting from initial temperature of 300K. Find `DeltaH` for the process
View SolutionWhich of the following representation is not correct for the change below? (Consider all substances at 0k are perfect crystals)
`{:(pA + qB,overset(Delta_(r )S_(1)^(9))rarr,underset((298K))(rC= sD)),(darr Delta_(r )S_(4),overset(Delta_(r )S_(3))rarr,uarr Delta_(r)S_(2)),(underset((0K))(pA + qB),,underset((0K))(rC=sD)):}`
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure = `P_(4)`, volume =`V_(1)` and absolute temperature =`T_(1)` expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are `P_(2), V_(2) and T_(2)`, respectively. For this expansion.
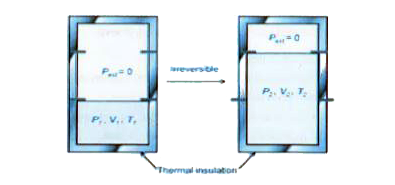
View SolutionMatch the following columns

View SolutionFor a perfectly cyrstalline solid `C_(p,m)= a T^(3) + bT`, where a and b are constants. If `C_(p,m)` is 0.40 J/K mol at 10K and 0.92 J/K mol at 20K, then molar entropy at 20K is `0.2x xx R` joules. Then the value of x is
View SolutionThe molar entropies of `HI_((g)), H_((g)) and I_((g))` at 298K are 206.5, 114.6, and `180.7 J mol^(-1)K^(-1)` respectively. Using the `DeltaG^(@)` given below, calculate the bond energy of HI.
`HI_((g)) rarr H_((g)) + I_((g)), DeltaG^(@) = 271.8kJ` (Give your answer after divide with 49.7)
View SolutionThe enthalpy changes of some process are given below
`alpha-D "glucose"_((s)) + H_(2)O rarr alpha -D- "glucose"_((aq))` Heat of dissolution =10.84kJ
`beta- D "glucose"_((s)) + H_(2)O rarr beta- D- "glucose"_((aq))` Heat of dissolution = 4.68kJ
`alpha-D "glucose"_((aq)) rarr beta - D- "glucose"_((aq)` Heat of mutarotation `=-1.16kJ`
The `DeltaH^(0) "for " alpha - D "glucose"_((s)) rarr beta -D "glucose"_((s))` is
View SolutionThe number of correct statements among the following
1 The expansion work for a gas into vacuum is equal to zero.
2. 1 mole of a gas occupying 3 litre volume on expanding to 15 litre at constant pressure of 1 atm does expansion work 1.215kJ.
3. The maximum work done by the gas during reversible expansionof 16g `O_(2)` at 300K from `5dm^(3)` to `25dm^(3)` is 2.0074 kJ.
4. The `DeltaS "for " s rarr l` is almost negligible in comparison to `DeltaS` for `l rarr g`.
5. `DeltaS= 2.303 nR "log" (V_(2))/(V_(1))` (at constant T)
6. Reversible isothermal work done `= -2.303nRT "log"_(10) (V_(2))/(V_(1))`
View SolutionIn a particular experiment, a gas undergoes adiabatic expansion satisfying the equation `VT^(3)=` constant. The ratio of specific heats is g then the value of 3g is
View Solution
Practice Sheet- Exercise-IV questions and complete solutions for chapter CHEMICAL THERMODYNAMICS of JEE (MAIN AND ADVANCED) CHEMISTRY of Class 12