Complete Solutions to NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (COLLISIONS) of chapter WORK, ENERGY AND POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, ENERGY AND POWER |
| MTG GUIDE | NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (COLLISIONS) |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
The coefficient of restitution for a perfectly elastic collision is
View SolutionA sphere of mass m moving with a constant velocity u hits another stationary sphere of the same mass and of coefficient of restitution (e). The ratio of velocities of the two spheres, after collision, will be
View SolutionA particle strikes a horizontal frictionless floor with a speed u at an angle `theta` with the vertical, and rebounds with a speed v at an angle `phi` with vertical. The coefficient of restitution between the particle and floor is e. The magnitude of v is
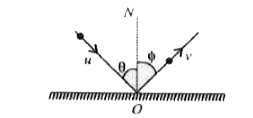
View SolutionA ball moving with a velocity of 6 m/s strikes an identical stationary ball. After collision each ball moves at angle of `30^@` with the original line of motion. Assuming that the collision is elastic, what are the speeds of the balls after the collision?
View SolutionTwo masses m, and m, moving with velocities `v_a and v_b` in opposite direction collide elastically and after the collision `m_a and m_b` move with velocities `v_b and v_a` respectively. Then the ratio `(m_a)/(m_b)` is
View SolutionA particle falls from a height h on a fixed horizontal plate and rebounds. If e is the coefficient of restitution, the total distance travelled by the particle before it stops rebounding is
View SolutionA particle strikes a horizontal frictionless floor with a speed u at an angle `theta` with the vertical, and rebounds with a speed v at an angle `phi` with vertical. The coefficient of restitution between the particle and floor is e. The angle `phi` is equal to
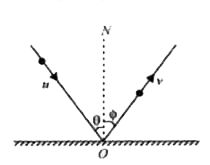
View SolutionA body of mass m moving with a uniform velocity of `40 m s^(-1)` collides with another body of mass m, at rest and then the two together begin to move with a uniform velocity of `30 m s^(-1)` The ratio of their masses `((m_1)/(m_2))` is
View SolutionParticle A makes a perfectly elastic collision with another particle B at rest. They fly apart in opposite directions with equal speeds. The ratio of their masses `m_A//m_B` is
View SolutionA bullet of mass M hits a block of mass M.. The transfer of energy is maximum, when
View SolutionA ball impinges directly on a similar ball at rest. The first ball is brought to rest by the impact. If half of the kinctic energy is lost by impact, the value of coefficient of restitution is
View SolutionA ball of mass m moving with a speed v makes a head on collision with an identical ball at rest. The kinetic energy after collision of the balls is three fourth of the original kinetic energy. The coefficient of restitution is
View SolutionA ball is dropped on to a horizontal plate from a height h = 9 m above it. If the coefficient of restitution is e = 1/2, the total distance travelled before the ball comes to rest is
View SolutionTwo identical spheres P and I lie on a smooth horizontal circular groove at opposite ends of diameter. Pis projected along the groove and at the end of time t, impinges on Q. If e is coefficient of restitution, the second impact will occur after a shortest time of
View SolutionWhen two spheres of equal masses undergo glancing clastic collision with one of them at rest, after collision they will move
View SolutionA light particle moving horizontally with a speed of 12 m/s strikes a very heavy block moving in the same direction at 10 m/s. The collision is one dimensional and elastic. After the collision, the particle will be

View SolutionA 10 kg object collides with a stationary 5 kg object and after collision, they stick together and move forward with velocity `4 ms^(-1)`. What is the velocity with which the 10 kg object hits the second one ?
View SolutionTwo particles having position vectors `vec(r_1) = (3hati +5hatj) m` and `vec(r_2) =(-5hati-3hatj)` m are moving with velocities `vec(v_1) = (4hati +3hatj)ms^(-1)` and `vec(v_2) = (a hati + 7 hatj) ms^(-1).` If they collide after 2 seconds, the value of a is
View SolutionThree identical spherical balls A, B and C are placed on a table as shown in the figure along a straight line. B and Care at rest initially.

The ball A hits B head on with a speed of `10 ms^(-1)`. Then after all collisions (assumed to be elastic) A and B are brought to rest and C takes off with a velocity of
View SolutionWhich of the following statements is correct?
View SolutionA block of mass 0.50 kg is moving with a speed of `2.00 m s^(-1)` on a smooth surface. It strikes another mass of 1.00 kg which is at rest and then they move together as a single body. The energy which is lost during the collision is
View SolutionIf two bodies stick together after collision and move as a single body, the collision is said to be
View SolutionThe first ball of mass m moving with a velocity u collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, the ratio of final velocity of the second ball to the initial velocity of the first ball is
View SolutionBall 1 collides with an another identical ball 2 at rest as shown in figure. For what value of coefficient of restitution e, the velocity of ball 2 becomes two times that of ball I after collision?

View SolutionA metal ball of mass 2 kg moving with speed of `36 km h^(-1)` has a head on collision with a stationary ball of mass 3 kg. If after collision, both the balls move together, then the loss in kinetic energy due to collision is
View SolutionA 2 kg ball moving at `24 ms^(-1)` undergoes head on collision with a 4 kg ball moving in the opposite direction at `48 m s^(-1)`. If the coefficient of restitution is `2/3`, their velocities in `m s^(-1)` after collision are
View SolutionA particle of mass m moving towards the east with speed v collides with another particle of the same mass and same speed v moving towards the north. If the two particles stick to each other, the new particle of mass 2m will have a speed of
View SolutionA mass m moves with a velocity v and collides inelastically with another identical mass at rest. After collision, the first mass moves with velocity `v/(sqrt3)` in a direction perpendicular to Before collision the initial direction of motion. The speed of the `2^(nd)` mass after collision
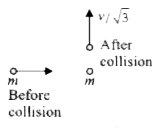
View SolutionA glass marble dropped from a certain height above the horizontal surface reaches the surface in time t and then continues to bounce up and down. The time in which the marble finally comes to rest is
(where e is the coefficient of restitution)
View SolutionTwo identical mass M moving with velocity `u_1 and u_2` collide perfectly inelastically. The loss in kinetic energy is
View SolutionIn elastic collision
View SolutionA car of mass 400 kg and travelling at `72 km h^(-1)` crashes into a truck of mass 4000 kg and travelling at `9 km h^(-1)` in the same direction. The car bounces back at a speed of `18 km h^(-1)`. The speed of the truck after the impact is
View SolutionA spherical ball A of mass 4 kg, moving along a straight line strikes another spherical ball B of mass 1 kg at rest. After the collision, A and B move with velocities `v_1 ms^(-1) and v_2 m s^(-1)` respectively making angles of `30^@` and `60^(@)` with respect to the original direction of motion of A. The ratio `(v_1)/(v_2)` will be
View SolutionA bullet of mass in travelling with a speed v hits a block of mass M initially at rest and gets embedded in it. The combined system is free to move and there is no other force acting on the system. The heat generated in the process will be
View SolutionA body of mass 1.0 kg strikes elastically with another body at rest and continues to move in the same direction with one-fourth of its initial velocity. The mass of the other body is
View Solution
NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (COLLISIONS) questions and complete solutions for chapter WORK, ENERGY AND POWER of MTG GUIDE PHYSICS (HINGLISH) of Class 11
All Exercises from MTG GUIDE Class 11 PHYSICS WORK, ENERGY AND POWER
- AIPMT/NEET (MCQs)
- CHECK YOUR NEET VITALS
- ILLUSTRATIONS
- NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (COLLISIONS)
- NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (CONSERVATION OF MECHANICAL ENERGY)
- NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (KINETIC ENERGY)
- NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (MOTIN IN A VERTICAL CIRCLE)
- NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (POTENTIAL ENERGY AND CONSERVATIVE FORCES)
- NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (POWER)
- NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (WORK - ENERGY THEOREM)
- NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (WORK DONE BY A CONSTANT FORCE AND VARIABLE FORCE)