Complete Solutions to COMPETITION FILE ( B.(MULTIPLE CHOICE QUESTIONS)) of chapter MOTION IN A STRAIGHT LINE of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN A STRAIGHT LINE |
| MODERN PUBLICATION | COMPETITION FILE ( B.(MULTIPLE CHOICE QUESTIONS)) |
| Number Of Questions | 74 |
| Academic Year | 2023-24 |
A bus begins to move with an accelaration of ` 1 ms^(-1)` . A man who is `48m` behind the bus starts running at ` 10 ms^(-1)` to catch the bus, the man will be able to catch the bus after .
View SolutionA particle is thrown vertically upward. Its velocity at half of the height is 10 m/s. Then the maximum height attained by it : -
`(g=10 m//s^2)`
View SolutionA stone is dropped from rest from the top of a tower 19.6m high. The distance travelled during the last second of its fall is (given `g=9.8m//s^(2)`):
View SolutionA 120 m long train is moving towards west with a speed of 10 `m//s`. A bird flying towards east with a speed of 5 `m//s` crosses the train. The time taken by the bird to cross the train will be
View SolutionA stone dropped from a building of height `h` and it reaches after `t` second on the earth. From the same building if two stones are thrown (one upwards and other downwards) with the same speed and they reach the earth surface after `t_(1)` and `t_(2)` seconds, respectively, then
View SolutionIf a ball is thrown vertically upwards with speed `u`, the distance covered during the last `t` second of its ascent is
View SolutionA body is moving with uniform acceleration describes 40 m in the first 5 sec and 65 m in next 5 sec. Its initial velocity will be
View SolutionA man throws balls with the same speed vertically upwards one after the other at an interval of 2s. What should be the speed of the throw so that more than two balls are in the sky at any time ? (Given `g = 9.8 m//s^(2)`)
View SolutionA bullet loses ` 1//20` of its velocity in passing through a plank. What is the least number of plankd required to stop the bullet .
View SolutionThe displacement x of a particle varies with time as `x=a e^(alphat)+be^(betat)` where a,b,a, `beta` are constants and are positives. The velocity of the particle will:
View SolutionA particle moves in a straight line with a constant acceleration. It changes its velocity from `10 ms^-1` to `20 ms^-1` while passing through a distance `135 m` in `t` seconds. The value of `t` is.
View SolutionThe distance travelled by a particle starting from rest and moving with an acceleration `(4)/(3) ms^-2`, in the third second is.
View SolutionA particle moves along a straight line `OX`. At a time `t` (in seconds) the distance `x` (in metre) of the particle is given by `x = 40 +12 t - t^3`. How long would the particle travel before coming to rest ?
View SolutionTwo bodies are dropped from two different building, one at a height 200m and another at a height of 150m above the ground. What will be difference in height of the bodies after they have fallen for 2s? `(g=10m//s^(2))`
View SolutionThe position x of a particle with respect to time t along x-axis is given by `x=9t^(2)−t^(3)` where x is in metres and t is in seconds. What will be the position of this pariticle when it achieves maximum speed along the + x direction ?
View SolutionA car accelerates from rest at constant rate for the first 10 s and covers a distance x. It covers a distance y in the next 10 s at the same acceleration. Which of the following is true?
View SolutionA car moves from `X` to `Y` with a uniform speed `v_u` and returns to `Y` with a uniform speed `v_d`. The average speed for this round trip is :
View SolutionA particle moving along x-axis has acceleration `f`, at time `t`, given by `f = f_0 (1 - (t)/(T))`, where `f_0` and `T` are constant.
The particle at `t = 0` has zero velocity. In the time interval between `t = 0` and the instant when `f = 0`, the particle's velocity `(v_x)` is :
View SolutionA paricle starting from the origin (0,0) moves in a straight line in `(x,y)` plane. Its coordinates at a later time are `(sqrt(3),3)`. The path of the particle makes with the x-axis an angle of
View SolutionA particle starts its motion from rest under the action of a constant force. If the distance covered in first `10 s` is `s_1` and the covered in the first `20 s` is `s_2`, then.
View SolutionA bus is moving with a speed of `10 m s^(-1)` on a straight road. A scooterist wishes to overtake the bus in 100 s. If the bus is at a distance of 1 km from the scooteritst with what speed should the scooterist chase the bus?
View SolutionA ball is droped from a high rise platform `t = 0` starting from rest. After `6 s` another ball is thrown downwards from the same platform with a speed `v`. The two balls meet at `t = 18 s`. What is the value of `v` ?
View SolutionA particle move a distance `x` in time `t` according to equation `x = (t + 5)^-1`. The acceleration of particle is alphaortional to.
View SolutionA body `A` starts from rest with an acceleration `a_1`. After `2` seconds, another body `B` starts from rest with an acceleration `a_2`. If they travel equal distances in the `5th` second, after the start of `A`, then the ratio `a_1 : a_2` is equal to :
View SolutionA ball dropped from 9th stair of multi storied building reaches the ground in 3 sec. In the first second of its free fall, it passes through n stairs then n equal to
View SolutionOne car moving on a staright road covers one-third of the distance with 20 `(km)/(hr)` and the rest with 60 `(km)/(hr)`. The average speed is
View SolutionA particles starts from rest and has an acceleration of ` 2m//s^(2)` for 10 sec. After that , it travels for 30 sec with constant speed and then undergoes a retardation of ` 4m//s^(2)` and comes back to rest. The total distance covered by the particle is
View SolutionA very large number of balls are thrown vertically upwards in quick successions in such a way that the next ball is thrown when the previous one is at the maximum height. If the maximum height is 5m, then number of balls thrown per minute is (take `g=10m//s^(2)`)
View SolutionThe position x of a particle varies with time t as `x=a t^(2)-b`. For what value of t acceleration is zero?
View SolutionA ball is thrown vertically upwards. Which of the following plots represents the speed-time graph of the ball during its height if the air resistance is ignored ?
View SolutionA body falls from a height `h = 200 m` (at New Delhi). The ratio of distance travelled in each `2 sec` during `t = 0` to `t = 6` seconds of the journey is.
View SolutionWhich of the following velocity-time graphs shows a realistic situation for a body in motion ?
View SolutionWhen a ball is thrown up vertically with velocity `v_0`, it reaches a maximum height of h. If one wishes to triple the maximum height then the ball should be thrown with velocity
View SolutionA particle shows distance-time curve as given in this figure. The maximum instantaneous velocity of the particle is around the point.
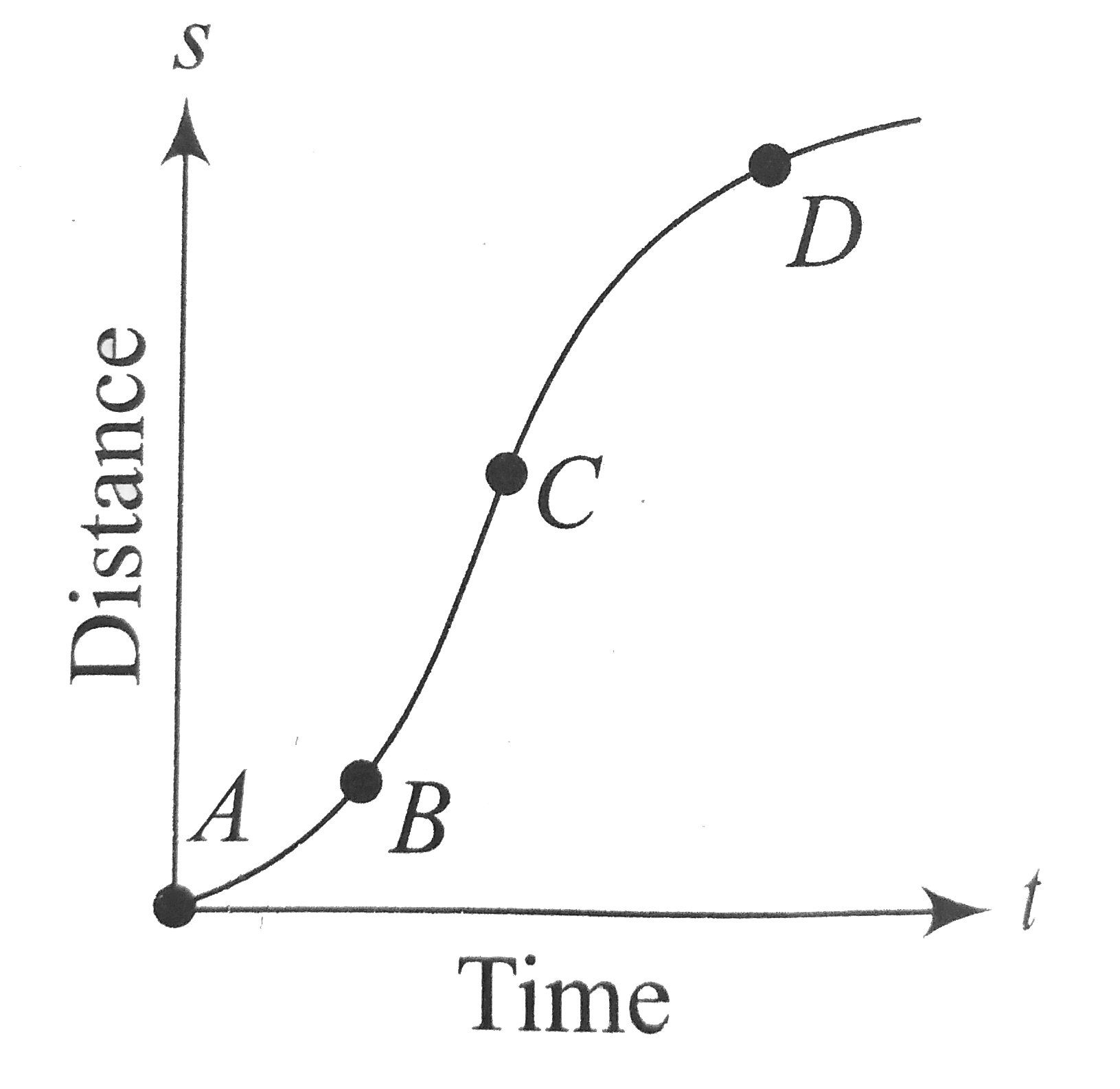 .
.
View SolutionA car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate `beta` to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
View SolutionA boy standing at the top of a tower of 20m of height drops a stone. Assuming `g=10ms^(-2)`, the velocity with which it hits the ground is :-
View SolutionThe motion of a particle along a straight line is described by equation : `x = 8 + 12 t - t^3` where `x` is in metre and `t` in second. The retardation of the particle when its velocity becomes zero is.
View SolutionA stone falls freely under gravity. It covered distances `h_1, h_2` and `h_3` in the first `5` seconds. The next `5` seconds and the next `5` seconds respectively. The relation between `h_1, h_2` and `h_3` is :
View SolutionA particle of unit mass undergoes one-dimensional motion such that its velocity varies according to
`v(x) = beta x^(-2 n)`
where `beta` and `n` are constant and `x` is the position of the particle. The acceleration of the particle as a function of `x` is given by.
View SolutionIf the velocity of a particle is `v = At + Bt^2`, where `A` and `B` are constant, then the distance travelled by it between `1 s` and `2 s` is :
View SolutionA car moves a distance of ` 200 m`. It covers the first half of the distance at speed of ` 40 km//h` and second half of the distance at a speed (v). The average speed is ` 48 km//h`. Find the value of (v) .
View SolutionA body travels such that square of time is proportional to the displacement. Its acceleration is:
View SolutionA body is vertically projected at 100 `ms^(-1)`. It returns after (`g=10 ms^(-2)`)
View SolutionA bo walks to his school at a distance of 6 km with constant speed of `2.5 kmh^(-1)` and walks back with a constant speed of `4 kmh^(-1)`. His average speed for round trip expressed in `kmh^(-1)`, is
View SolutionA ball of mass `m_(1)` and another ball of mass `m_(2)` are dropped from equal height. If the time taken by the balls are `t_(1)` and `t_(2)`, respectively, then
View SolutionA ball is dropped on the floor from a height of 10m. It rebounds to a height of 2.5 m if the ball is in contact with floor for 0.01 s then the average acceleration during contact is nearly
View SolutionA cyclist acceleration from rest to a velocity of `72 km hr^(-1)` in 10sec. If the cyclist is in straight track the acceleration of the cyclist is:
View SolutionA car has speed of 40km/h. on applying brakes it stops after 15m. If its speed was 80 `km h^(-1)` it would have stopped after
View SolutionA particle is moving such that its position coordinates `(x, y)` are `(2m, 3m)` at time `t=0, (6m, 7m)` at time `t=2 s`, and `(13 m, 14m)` at time `t=5 s`.
Average velocity vector`(vec(V)_(av))` from `t=0` to `t=5 s` is
View SolutionPreeti reached the metro station and found that the escalator was not working. She walked up the stationary escalator in time `t_1`. On other days, if the remains stationary on the moving escalator, then the escalator takes her up in time `t_2`. The time taken by her to walk up on the moving escalator will be :
View SolutionThe x and y coordinates of the particle at any time are `x=5t-2t^(2) and y=10t` respectively, where x and y are in meters and t in seconds. The acceleration of the particle at t=2s is:
View SolutionA person travelling on a straight line moves with a uniform velocity `v_1` for a distance x and with a uniform velocity `v_2` for the next equal distance. The average velocity v is given by
View SolutionA parachutist after bailing out falls 50m without friction. When parachute opens, it decelerates at `2m//s^2`. He reaches the ground with a speed of `3m//s`. At what height, did the bail out?
View SolutionIn a car race, car A takes a time t less than car B at the finish and passes the finishing point with speed v more than that of the car B. Assuming that both the cars start from rest and travel with constant acceleration `a_1 and a_2` respectively. Show that `v=sqrt (a_1 a_2) t.`
View SolutionAn automobile travellingat `40 km//h`, can be stopped at distance of 40 m by applying brakes. If the same autombile is travelling at`80 km//h`, the minimum stopping distance, in metres is (assume no skidding) :
View SolutionAll the graphs below are intended to represent the same motion. One of them does it incorrectly. Pick it up.
View SolutionThe velocity of particle is `v=v_(0)+"gt"+ft^(2)`. If its position is `x=0` at `t=0` then its displacement after unit time `(t=1)` is
View SolutionAn object , moving with a speed of ` 6.25 m//s `, is decelerated at a rate given by :
`(dv)/(dt) = - 2.5 sqrt (v)` where `v` is the instantaneous speed . The time taken by the object , to come to rest , would be :
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in `T/3` second?
View SolutionA particle of mass m is acted upon by a force F given by the emprical law `F=(R)/(t^2)upsilon(t)`
If this law is to be tested experimentally by observing the motion starting from rest, the best way is to plot :
View SolutionFrom a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is
View SolutionA person climbs up a stalled escalator in 60s. If standing on the same but escalator running with constant velocity, he takes 40 s. How much time is taken by the person to walk up the moving escalator?
View SolutionThe velocity-time graphsof a car and a scooter are shown in the figure. (i) The difference between the distance travelled by the car and the scooter in 15 and (ii) the time at which the car will catch up with the scooter are, respectively.
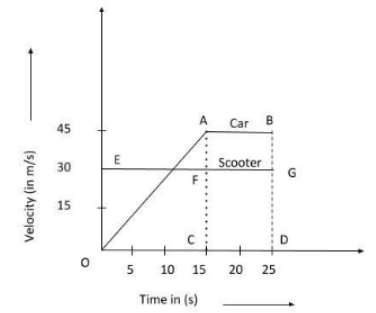
View SolutionTwo stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . ` g= 10 m//s^(2) ` (The figures are schematic and not drawn to scale)
View SolutionWhich of the following option correctly describes the variation of the speed ` ` and acceleration `'a'` of a point mass falling vertically in a viscous medium that applies a force `F=-kv`, where `'k'` is constant, on the body?
(Graphs are schematic and drawn to scale)
View SolutionA car moving with a velocity of `20ms^(-1)` is stopped in a distance of 40m. If the same car is travelling at double the velocity, the distance travelled by it for same retardation is
View SolutionA car is standing 200m behind a bus , which is also at rest . The two. Start moving at the same instant but with different forward accelerations. The bus has acceleration `2 ms ^(-2)` and The car has acceleration `4 ms^(-2)` The car will catch up will the bus after time :
View SolutionWhich graph corresponds to an object moving with a constant negative acceleration and a positive velocity ?
View SolutionA body is thrown vertically upwards. Which one of the following graphs correctly represent the velocity vs time?
View SolutionDisplacement (x) of a particle is related to time (t) as
`x = at + b t^(2) - c t^(3)`
where a,b and c are constant of the motion. The velocity of the particle when its acceleration is zero is given by:
View SolutionA particle starting from rest. Its acceleration (a) versus time (t) is as shown in the figure.
The maximum speed of the particle will be.
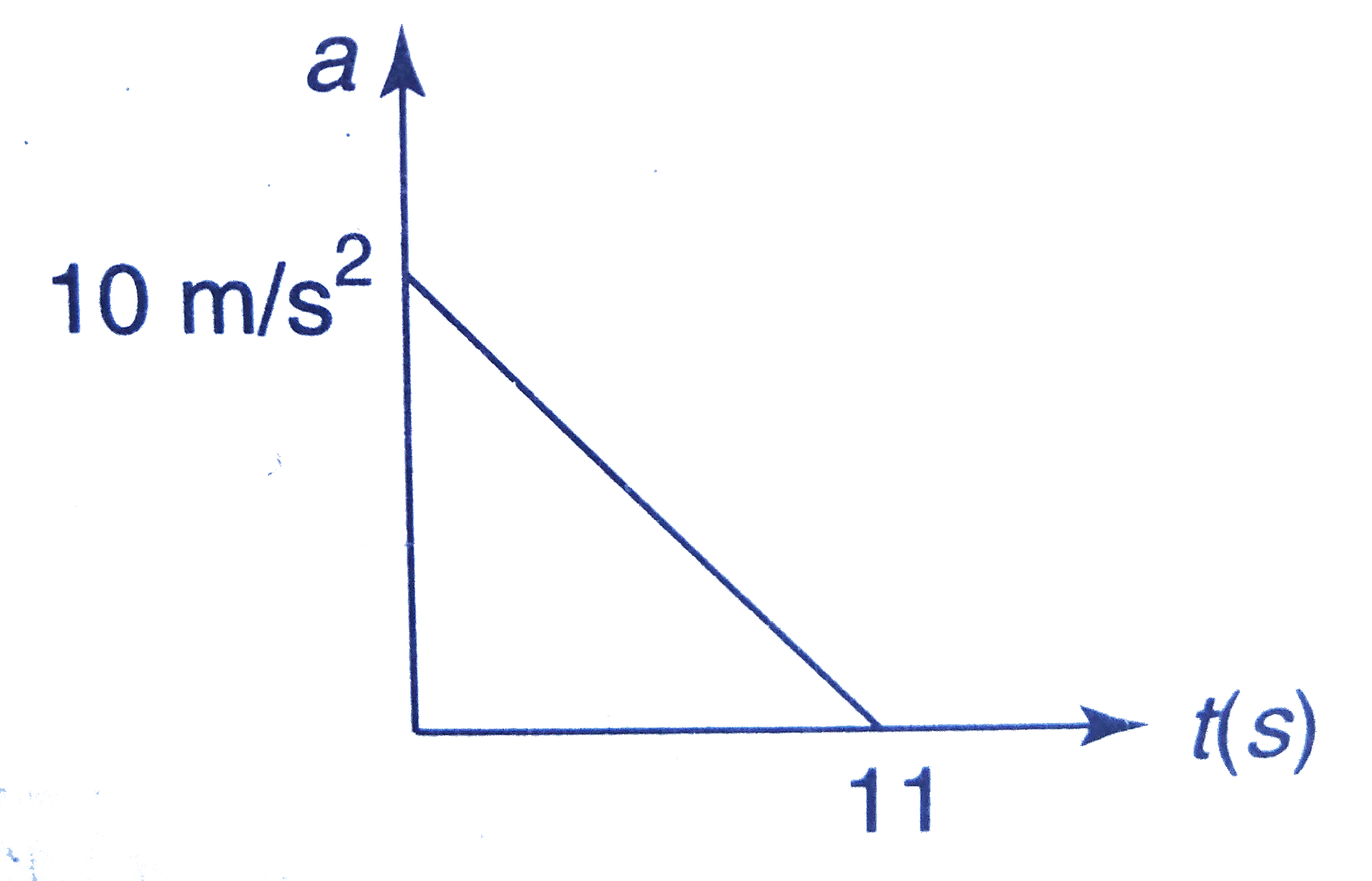
View SolutionA small block slides without friction down an iclined plane starting form rest. Let `S_(n)` be the distance traveled from time `t = n - 1` to `t = n`. Then `(S_(n))/(S_(n + 1))` is:
View SolutionA tennis ball dropped on a barizoontal smooth surface , it because back to its original postion after hiting the surface the force on the bell during the collision is propertional to the length of compression of the bell . Which one of the following skethes desches discribe the variation of its kinetic energy `K` with time `1` mass apporiandly ? The figure as only illistrative and not to the scale .
View SolutionConsider an expanding sphere of instantaneous radius ? whose total mass remains constant. The expansion is such that the instantaneous density `rho` remains uniform throughout the volume. The rate of fractional change in density `((dp)/(rhodt))` is constant. The velocity v of any point on the surface of the expanding sphere is proportional to
View Solution
COMPETITION FILE ( B.(MULTIPLE CHOICE QUESTIONS)) questions and complete solutions for chapter MOTION IN A STRAIGHT LINE of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 11
All Exercises from MODERN PUBLICATION Class 11 PHYSICS MOTION IN A STRAIGHT LINE
- CHAPTER PRACTICE TEST
- COMPETITION FILE ( A.(MULTIPLE CHOICE QUESTIONS))
- COMPETITION FILE ( B.(MULTIPLE CHOICE QUESTIONS))
- COMPETITION FILE ( C.(MULTIPLE CHOICE QUESTIONS))
- COMPETITION FILE ( D.(MULTIPLE CHOICE QUESTIONS))
- COMPETITION FILE (ASSERTION REASON)
- COMPETITION FILE (INTEGER TYPE QUESTIONS )
- COMPETITION FILE (MATCHING TYPE QUESTIONS)
- COMPETITION FILE (MATRIX MATCH TYPE QUESTIONS )
- CONCEPTUAL QUESTIONS
- HIGHER ORDER THINKING SKILL AND ADVANCED LEVEL QUESTION WITH ANSWER
- NCERT (ADDITIONAL EXERCISE)
- NCERT (MULTIPLE CHOICE QUESTION (TYPE-I))
- NCERT (MULTIPLE CHOICE QUESTION (TYPE-II))
- NCERT (SHORT ANSWER TYPE QUESTION)
- NCERT (TEXTBOOK EXERCISES )
- NCERT (VERY SHORT ANSWER TYPE QUESTION)
- PRACTICE PROBLEMS
- REVISION EXERCISE (FILL IN THE BLANKS)
- REVISION EXERCISE (LONG ANSWER QUESTIONS)
- REVISION EXERCISE (NUMERICAL PROBLEMS )
- REVISION EXERCISE (SHORT ANSWER QUESTIONS)
- REVISION EXERCISE (VERY SHORT ANSWER QUESTION)
- SOLVED EXAMPLE
- TOUGH & TRICKY ( PROBLEMS)