Complete Solutions to LECTURE SHEET - EXERCISE - III (LEVEL - II ADVANCED)(LINKED COMPREHENSION TYPE QUESTIONS) of chapter STATES OF MATTER of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | STATES OF MATTER |
| AAKASH SERIES | LECTURE SHEET - EXERCISE - III (LEVEL - II ADVANCED)(LINKED COMPREHENSION TYPE QUESTIONS) |
| Number Of Questions | 6 |
| Academic Year | 2023-24 |
According to Maxwell distribution, the area under the curve is equal to the total number of molecules in collision. On increasing temperature, fraction of molecules having speed equal to `u_(mp)` .(most probable speed) decreases. The speed distribution also depends on the mass of the molecules along with the temperature. In general, the distribution depends upon the value of `M/T ` (where M is molar mass and Tis temperature in kelvin).
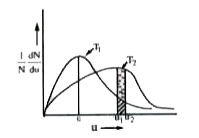
Relationship between `T_1` and `T_2` is given as
View SolutionAccording to Maxwell distribution, the area under the curve is equal to the total number of molecules in collision. On increasing temperature, fraction of molecules having speed equal to `u_(mp)` .(most probable speed) decreases. The speed distribution also depends on the mass of the molecules along with the temperature. In general, the distribution depends upon the value of `M/T` (where M is molar mass and Tis temperature in kelvin).
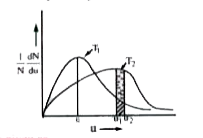
On increasing the temperature, number of molecules having speed between `u_1 and u_2`
View SolutionAccording to Maxwell distribution, the area under the curve is equal to the total number of molecules in collision. On increasing temperature, fraction of molecules having speed equal to `u_(mp)` .(most probable speed) decreases. The speed distribution also depends on the mass of the molecules along with the temperature. In general, the distribution depends upon the value of `M/T` (where M is molar mass and Tis temperature in kelvin).
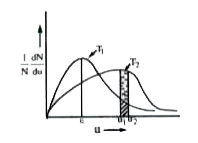
If at `T_1 K` is u, then value of `u_(rms)` at `T_2` is
View SolutionThe root mean square speed of an ideal gas is given by : `u_("rms") = sqrt((3RT)/M)` Thus we conclude that `u_("rms")` speed of the ideal gas molecules is proportional to square root of the temperature and inversely proportional to the square root of the molar mass. The translational kinetic energy per mole can also be given as `1/2Mu_(rms)^(2)` . The mean free path (`lambda`) is the average of distances travelled by molecules in between two successive collisions whereas collision frequency (C.F.) is expressed as number of collisions taking place in unit time. The two terms `lambda` and C.F. are related by : `C.F = (u_("rms")/lambda)`
A jar contains He and H, in the molar ratio 1 : 5. The ratio of mean translational kinetic energy at the same temperature is
View SolutionThe root mean square speed of an ideal gas is given by : `u_("rms") = sqrt((3RT)/M)` Thus we conclude that `u_("rms")` speed of the ideal gas molecules is proportional to square root of the temperature and inversely proportional to the square root of the molar mass. The translational kinetic energy per mole can also be given as `1/2Mu_(rms)^(2)` . The mean free path (`lambda`) is the average of distances travelled by molecules in between two successive collisions whereas collision frequency (C.F.) is expressed as number of collisions taking place in unit time. The two terms `lambda` and C.F. are related by : `C.F = (u_("rms")/lambda)`
Which of the following relation is correct for an ideal gas regarding its pressure (P) and translational kinetic energy per unit volume (E) ?
View SolutionThe root mean square speed of an ideal gas is given by : `u_("rms") = sqrt((3RT)/M)` Thus we conclude that `u_("rms")` speed of the ideal gas molecules is proportional to square root of the temperature and inversely proportional to the square root of the molar mass. The translational kinetic energy per mole can also be given as `1/2Mu_(rms)^(2)` . The mean free path (`lambda`) is the average of distances travelled by molecules in between two successive collisions whereas collision frequency (C.F.) is expressed as number of collisions taking place in unit time. The two terms `lambda` and C.F. are related by : `C.F = (u_("rms")/lambda)`
If n represents number of moles, n0 is number of molecules per unit volume, k is Boltzmann constant, R is molar gas constant, T is absolute temperature and NA is Avogadro's number then which of the following relations is wrong ?
View Solution
LECTURE SHEET - EXERCISE - III (LEVEL - II ADVANCED)(LINKED COMPREHENSION TYPE QUESTIONS) questions and complete solutions for chapter STATES OF MATTER of JEE (MAIN AND ADVANCED) CHEMISTRY of Class 11
All Exercises from AAKASH SERIES Class 11 CHEMISTRY STATES OF MATTER
- ADDITIONAL PRACTICE EXERCISE (LEVEL - I MAIN) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE (LEVEL - II)(LECTURE SHEET ADVANCED) (LINKED COMPREHENSION TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE (LEVEL - II)(LECTURE SHEET ADVANCED) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE (LEVEL - II)(LECTURE SHEET ADVANCED) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE (LEVEL - II)(PRACTICE SHEET ADVANCED) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
- ADDITIONAL PRACTICE EXERCISE (LEVEL - II)(PRACTICE SHEET ADVANCED) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
- LECTURE SHEET - EXERCISE - I (LEVEL - I MAIN)(STRAIGHT OBJECTIVE TYPES QUESTIONS)
- LECTURE SHEET - EXERCISE - I (LEVEL - II ADVANCED)(INTEGER TYPE QUESTIONS)
- LECTURE SHEET - EXERCISE - I (LEVEL - II ADVANCED)(LINKED COMPREHENSION TYPES QUESTIONS)
- LECTURE SHEET - EXERCISE - I (LEVEL - II ADVANCED)(MATRIX MATCHING TYPE QUESTIONS)
- LECTURE SHEET - EXERCISE - I (LEVEL - II ADVANCED)(MORE THAN ONE CORRECT ANSWER TYPES QUESTIONS)
- LECTURE SHEET - EXERCISE - I (LEVEL - II ADVANCED)(STRAIGHT OBJECTIVE TYPES QUESTIONS)
- LECTURE SHEET - EXERCISE - II (LEVEL - I MAIN)(STRAIGHT OBJECTIVE TYPES QUESTIONS)
- LECTURE SHEET - EXERCISE - II (LEVEL - II ADVANCED)(INTEGER TYPE QUESTIONS)
- LECTURE SHEET - EXERCISE - II (LEVEL - II ADVANCED)(MATRIX MATCHING TYPE QUESTIONS)
- LECTURE SHEET - EXERCISE - II (LEVEL - II ADVANCED)(MORE THAN ONE CORRECT ANSWER TYPES QUESTIONS)
- LECTURE SHEET - EXERCISE - II (LEVEL - II ADVANCED)(STRAIGHT OBJECTIVE TYPES QUESTIONS)
- LECTURE SHEET - EXERCISE - III (LEVEL - I MAIN)(STRAIGHT OBJECTIVE TYPE QUESTIONS)
- LECTURE SHEET - EXERCISE - III (LEVEL - II ADVANCED)(INTEGER TYPE QUESTIONS)
- LECTURE SHEET - EXERCISE - III (LEVEL - II ADVANCED)(LINKED COMPREHENSION TYPE QUESTIONS)
- LECTURE SHEET - EXERCISE - III (LEVEL - II ADVANCED)(MATRIX MATCHING TYPE QUESTIONS)
- LECTURE SHEET - EXERCISE - III (LEVEL - II ADVANCED)(MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
- LECTURE SHEET - EXERCISE - III (LEVEL - II ADVANCED)(STRAIGHT OBJECTIVE TYPE QUESTIONS)
- LECTURE SHEET - EXERCISE - IV (LEVEL - I MAIN)(STRAIGHT OBJECTIVE TYPE QUESTIONS)
- LECTURE SHEET - EXERCISE - IV (LEVEL - II ADVANCED)(INTEGER TYPE QUESTIONS)
- LECTURE SHEET - EXERCISE - IV (LEVEL - II ADVANCED)(LINKED COMPREHENSION TYPE QUESTIONS)
- LECTURE SHEET - EXERCISE - IV (LEVEL - II ADVANCED)(MATRIX MATCHING TYPE QUESTIONS)
- LECTURE SHEET - EXERCISE - IV (LEVEL - II ADVANCED)(MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
- LECTURE SHEET - EXERCISE - V (LEVEL - I MAIN)(STRAIGHT OBJECTIVE TYPE QUESTIONS)
- OBJECTIVE EXERCISE - 1 (GAS LAWS)
- OBJECTIVE EXERCISE - 1 (GRAHAM.S LAW)
- OBJECTIVE EXERCISE - 1 (INTERMOLECULAR FORCES)
- OBJECTIVE EXERCISE - 1 (INTRODUCTION)
- OBJECTIVE EXERCISE - 1 (KINETIC THEORY OF GASES)
- OBJECTIVE EXERCISE - 1 (LIQIFICATION OF GASES AND CRITICAL CONSTANTS)
- OBJECTIVE EXERCISE - 1 (SURFACE TENSION)
- OBJECTIVE EXERCISE - 1 (TYPES OF VELOCITIES)
- OBJECTIVE EXERCISE - 1 (VAN DER WAAL EQUATIONS)
- OBJECTIVE EXERCISE - 1 (VISCOSITY)
- OBJECTIVE EXERCISE - 2 (DALTON.S LAW)
- OBJECTIVE EXERCISE - 2 (GAS LAWS)
- OBJECTIVE EXERCISE - 2 (GRAHAM.S LAW)
- OBJECTIVE EXERCISE - 2 (INTERMOLECULAR FORCES)
- OBJECTIVE EXERCISE - 2 (KINETIC THEORY)
- OBJECTIVE EXERCISE - 2 (TYPES OF VELOCITIES)
- OBJECTIVE EXERCISE - 2 (VISCOSITY)
- OBJECTIVE EXERCISE -1
- OBJECTIVE EXERCISE -2
- OBJECTIVE EXERCISE -3
- PRACTICE EXERCISE
- PRACTICE SHEET (EXERCISE -I) (LEVEL -I MAINS)(STRAIGHT OBJECTIVE TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -I) (LEVEL -II ADVANCED)(INTEGER TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -I) (LEVEL -II ADVANCED)(LINKED COMPREHENSION TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -I) (LEVEL -II ADVANCED)(MATRIX MATCHING TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -I) (LEVEL -II ADVANCED)(MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -I) (LEVEL -II ADVANCED)(STRAIGHT OBJECTIVE TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -II) (LEVEL -I MAIN)(STRAIGHT OBJECTIVE TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -II) (LEVEL -II ADVANCED)(INTEGER TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -II) (LEVEL -II ADVANCED)(LINKED COMPREHENSION TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -II) (LEVEL -II ADVANCED)(MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -II) (LEVEL -II ADVANCED)(STRAIGHT OBJECTIVE TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -III) (LEVEL -I MAIN)(STRAIGHT OBJECTIVE TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -III) (LEVEL -II ADVANCED)(INTEGER TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -III) (LEVEL -II ADVANCED)(LINKED COMPREHENSION TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -III) (LEVEL -II ADVANCED)(MATRIX MATCHING TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -III) (LEVEL -II ADVANCED)(MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -III) (LEVEL -II ADVANCED)(STRAIGHT OBJECTIVE TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -IV) (LEVEL -I MAINS)(STRAIGTH OBJECTIVE TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -IV) (LEVEL -II ADVANCED)(INTEGER TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -IV) (LEVEL -II ADVANCED)(MATRIX MATCHING TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -IV) (LEVEL -II ADVANCED)(STRAIGTH OBJECTIVE TYPE QUESTIONS)
- PRACTICE SHEET (EXERCISE -V) (LEVEL -I MAIN)(STRAIGHT OBJECTIVE TYPE QUESTIONS)
- PROBLEMS
- SUBJECTIVE EXERCISE - 1 (NUMERICALS)
- SUBJECTIVE EXERCISE - 1 (SHORT ANSWER QUESTIONS)
- SUBJECTIVE EXERCISE - 1 (VERY SHORT ANSWER QUESTIONS)
- SUBJECTIVE EXERCISE - 2 (NUMERICALS)
- SUBJECTIVE EXERCISE - 2 (SHORT ANSWER QUESTIONS)
- SUBJECTIVE EXERCISE - 2 (VERY SHORT ANSWER QUESTIONS)
- SUBJECTIVE EXERCISE - 3 (NUMERICALS)
- SUBJECTIVE EXERCISE - 3 (SHORT ANSWER QUESTIONS)
- SUBJECTIVE EXERCISE - 3 (VERY SHORT ANSWER QUESTIONS)
- SUBJECTIVE EXERCISE -1 ( NUMERICALS)
- SUBJECTIVE EXERCISE -1 ( SHORT ANSWER QUESTIONS)
- SUBJECTIVE EXERCISE -1 ( VERY SHORT ANSWER QUESTIONS)
- SUBJECTIVE EXERCISE -2 ( NUMERICALS)
- SUBJECTIVE EXERCISE -2 ( SHORT ANSWER QUESTIONS)
- SUBJECTIVE EXERCISE -2 ( VERY SHORT ANSWER QUESTIONS)
- SUBJECTIVE EXERCISE -3 (SHORT ANSWER QUESTIONS)
- SUBJECTIVE EXERCISE -3 (VERY SHORT ANSWER QUESTIONS)