Complete Solutions to LONG ANSWER QUESTIONS of chapter HEIGHT AND DISTANCE of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | HEIGHT AND DISTANCE |
| VK GLOBAL PUBLICATION | LONG ANSWER QUESTIONS |
| Number Of Questions | 17 |
| Academic Year | 2023-24 |
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are `45o`and `60o`respectively. Find the height of the tower.
View SolutionA statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is `60o`and from the same point the angle of elevation of the top of the pedestal is `45o`. Find the height of
View SolutionFrom the top of a 7 m high building, the angle of elevation of the top of a cable tower is `60o`and the angle of depression of its foot is `45o`. Determine the height of the tower.
View SolutionAt a point, the angle of elevation of a tower is such that its tangent is `5/12`. On walking 240 m nearer to the tower, the tangent of the angle of elevation becomes `3/4`. Find the height of the tower.
View SolutionA 1.2 m tall girl spots a ballon moving with wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is `60^(@)`. After some time, the angle of elevation reduces to `30^(@)`. Find the distance travelled by the balloon during the interval.
View SolutionA straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of `30o` , which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depres
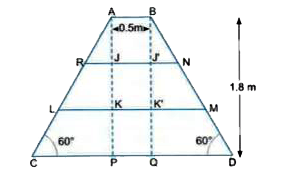
View SolutionIn fig ABDC is a trapezium in which `AB||CD`. Line segments RN and LM are drawn parallel to AB such that AJ=JK =KP. If AB=0.5m and AP=BQ=1.8m, find the length of AC, BD, RN and LM.
View SolutionTwo poles of equal heights are standing opposite to each other on either side of the road which is 80m wide. From a point between them on the road the angles of elevation of the top of the poles are `60o` and `30o` respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionA TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is `60o`. From another point 20 m away from this point on the line joining this point t
View SolutionA person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is `60^0dot` When he move 40 metres away from the bank, he finds the angle of elevation to be `30^0dot` Find the height of the tree and the width of the river.
View SolutionThe angles of elevation oand depression of the top and bottom of a lighthouse from the top of a building, 60 m high, are `30^(@)` and `60^(@)` respectively. Find
(i) the difference between the heights of the lighthouse and the building.
(ii) distance between the lighthouse and the building.
View SolutionFrom the top of a building AB, 60 metres hight, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be `30^(@)` and `60^(@)`, respectively. Find
(i) the horizontal distance between AB and CD.
(ii) the height of the lamp post.
View SolutionA boy standing on a horizontal plane finds a bird flying at a distance of 100 m from him at an elevation of 30°. A girl standing on the roof of 20 metre high building, finds the angle of elevation of the same bird to be 45°. Both the boy and the girl are on opposite sides of the bird. Find the distance of bird from the girl.
View SolutionThe angles of depression of the top and the bottom of an 8 m tall building from the top of a multi-storeyed building are `30o`and `45o`, respectively. Find the height of the multi-storeyed building and the distance between the two buildings.
View SolutionThe angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is `45^(@)`. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is `60^(@)`, then find the height of the flagstaff. [Use `sqrt(3) = 1.732`.]
View SolutionA round balloon of radius r subtends an angle` alpha` at the eye of the observer while the angle of elevation of its centre is `beta`. Prove that the height of the centre of the balloon is `r sin(beta) cosec(alpha)/2`
View SolutionA vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are `60^(@)` and `30^(@)` respectively. Find the height of the tower and the distance of the point from the tower. (Take `sqrt(3)=1.732`)
View Solution
LONG ANSWER QUESTIONS questions and complete solutions for chapter HEIGHT AND DISTANCE of VK GLOBAL PUBLICATION MATHS (HINGLISH) of Class 10
All Exercises from VK GLOBAL PUBLICATION Class 10 MATHS HEIGHT AND DISTANCE
- HOTS (HIGHER ORDER THINKING SKILLS)
- LONG ANSWER QUESTIONS
- PROFICIENCY EXERCISE ( LONG ANSWER QUESTIONS II)
- PROFICIENCY EXERCISE ( SHORT ANSWER QUESTIONS I)
- PROFICIENCY EXERCISE ( SHORT ANSWER QUESTIONS II)
- PROFICIENCY EXERCISE ( VERY SHORT ANSWER QUESTIONS I)
- SELF ASSESSMENT TEST
- SHORT ANSWER QUESTIONS I
- SHORT ANSWER QUESTIONS II
- VERY SHORT ANSWER QUESTIONS