Complete Solutions to MULTIPLE CHOICE QUESTIONS of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| MBD -HARYANA BOARD | MULTIPLE CHOICE QUESTIONS |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
Sides of two similar triangles are in the ratio `4:9` . Areas of these triangles are in the ratio. `2:3` (b) `4:9` (c) `81 : 16` (d) `16 : 81`
View SolutionThe areas of two similar `triangleABC and trianglePQR` are 64 sq. cm and 121 sq. cm. repsectively. If QR= 15.4 cm, find BC.
View SolutionTriangles ABC and DEF are similar. If area of `DeltaABC = 16 cm^2`, area of `DeltaDEF = 25 cm^2` and `BC = 2.3 cm,` then EF is :
View SolutionTriangle ABC and DEF are similar. If AC = 19 cm and DF = 8 cm , the ratio of the area of two triangles are :
View SolutionWhich one pair of the triangles is not similar triangles ?
View SolutionArea of two similar triangles are in the ratio of 5:3 then the ratio of their corresponding sides is :
View SolutionIn the given figure `Delta ODC ~ Delta OAB, /_BOC=100^@, /_ODC=60^@` then `/_OAB=`
View SolutionThe ratio of corresponding sides of two similar triangles is `2:3`, then the ratio of the perimeters of two triangles is `4:9` (True/False).
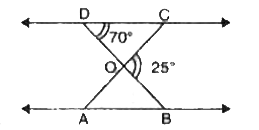
View SolutionIn the given figure `Delta ODC ~ Delta OAB , /_BOC= 125^@, /_ODC = 70^@`, then `/_OAB` is equal to :
View SolutionIf the ratio of the sides of two similar triangles is 3 : 5, then the ratio of their areas is :
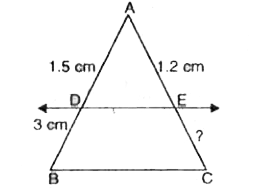
View SolutionIn the given figure `DE||BC`, then the value of DB is :
View SolutionAreas of two similar triangles are i the ratio of 4:5, then the ratio of their corresponding sides is :
View SolutionIn the given figure `DE||BC`, then the value of EC is :
View SolutionAreas of two similar triangles are i the ratio of 5:3, then the ratio of their corresponding sides is :
View SolutionIf the ratio of sides of two similar triangles is 2:5, then the ratio of their areas will be :
View SolutionIf in a triangle, square of one side is equal to the sum of squares of the other two sides, then the angle opposite the first side is :
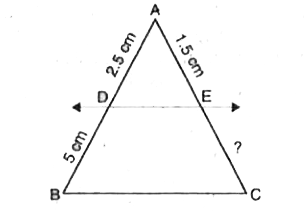
View SolutionIn figure, `DE||BE`, then EC will be :
View SolutionAreas of two similar triangles are in the ratio 64:121, then the sides of these triangles are in the ratio:
View SolutionSides of some triangles are given below:
(i) 5 cm, 12 cm , 15 cm
(ii) 5 cm , 6 cm , 8 cm
(iii) 8 cm, 15 cm , 17 cm .
Among these, right triangles is :
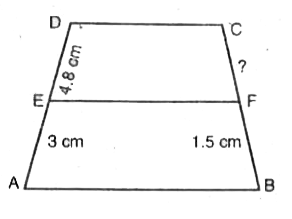
View SolutionABCD is a trapizium with `AB||DC`. E and F are points on non - parallel sides AD and BC respecitively such that `EF||AB`, If AE = 3cm, ED = 4.8 cm, BF = 1.5 cm, then the value of CF is :
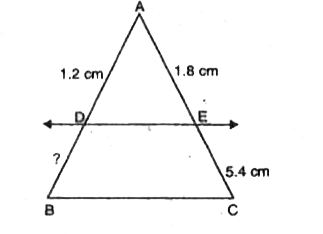
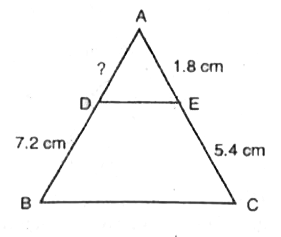
View SolutionIn figure, `DE||BC` and BD = 7.2 cm , CE = 5.4 cm and AE = 1.8 cm. Then AD is equal to :
View SolutionABC and BDE are two equilateral trainales, such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is :
View SolutionSides of triangles are given in options, which of them is a right triangle ?
View SolutionThe sides of two similar triangles are in the ratio 3:7. The ratio of areas of these triangles will be :
View Solution
MULTIPLE CHOICE QUESTIONS questions and complete solutions for chapter TRIANGLES of MBD NCERT SOLUTIONS of Class 10