Complete Solutions to PRACTICE THOROUGHLY of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| KUMAR PRAKASHAN | PRACTICE THOROUGHLY |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
In `DeltaABC`, D and E are points on the sides AB and AC respectively such that `DE||BC`. If `AB= 6.75 cm, AC= 8.50 cm" and "EC = 6.80 cm`. Then find BD.
View Solution`DeltaABC ~ DeltaPQR`. If `AB= 6.5 cm, PQ= 10.4 cm` and the perimeter of `DeltaABC` is 60 cm, then find the perimeter of `DeltaPQR`.
View SolutionIn `DeltaABC`, D and E are points of sides AB and AC such that `DE||BC`. If `AD= x, DB= 2x-1, AE= x+3` and EC= 2x, then find the value of x.
View SolutionAn aeroplane leaves an airport and flies due west at a speed of 2100 km per hour. At the same time, another aeroplane leaves the same airport and flies due south at a speed of 2000 km per hour. How far apart will be the two planes after `1` hours?
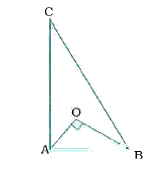
View SolutionIn the given figure, `OA= 3cm, OB= 4 cm, /_AOB= 90^(@), AC= 12 cm" and "BC= 13 cm`. Prove that `/_CAB= 90^(@)`.
View SolutionIn trapezium ABCD, `AB||CD` and `AB= (1)/(3)CD`. The diagonals AC and BD interset at O. If `ar (AOB)= 21 cm^(2)`, then find ar (COD).
View Solution`DeltaABC" and "DeltaDEF` are two equilateral triangles of sides 4 cm and 2 cm respectively. Find the ratio of ar(ABC) and ar(DEF).
View SolutionA girl of height 100 cm is walking away from the base of a lamp-post at a speed of `1.9m"/"s`. If the lamp is 5m above the ground, find the length of her shadow after 4 seconds.
View SolutionIn `triangleABC, /_C= 90^(@)` and P and Q are the midpoints of BC and AC respectively. Prove that `AP^(2)+ BQ^(2)= 5PQ^(2)`.
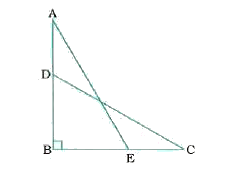
View SolutionIn the given figure, `/_B= 90^(@)`. If AE= CD= 13 cm and BE= AD= 5 cm, then find BC.
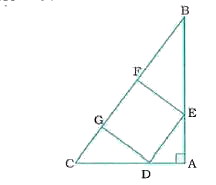
View SolutionIn the given figure, EFGD is a square and `/_BAC= 90^(@)`. Prove that `BF xx CG= GF^(2)`.
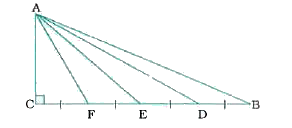
View SolutionIn right angled DeltaABC, `/_C= 90^(@)` and D, E, F are three points on BC such that they divide BC in eaual parts (see the given figure). Prove that `8(AF^(2)+AD^(2))= 11AC^(2)+5AB^(2)`.
View SolutionIn an equilateral ABC, E is a point on BC such that `BE= (1)/(4)BC`. Prove that `16AE^(2)= 13AB^(2)`.
View SolutionA rhombus has each side of length 20 cm and one pair of opposite angles `60^(@)` each. Find the length of its diagonals.
View SolutionIn `DeltaABC, /_B=90^(@)`. D and E are any points on sides AB and BC respectively. Prove that `AE^(2)+CD^(2)= AC^(2)+DE^(2)`.
View SolutionIn `DeltaABC, /_B= 90^(@)` and BM is an altitude. Prove that `(1)/(BM^2)= (1)/(AB^2)+(1)/(BC^2)`.
View SolutionABCD is a rhombus. Prove that `AB^(2)+BC^(2)+CD^(2)+DA^(2)= AC^(2)+BD^(2)`.
View SolutionIn equilateral DeltaABC, D is a point on BC such that `BD= (1)/(3)BC`. Prove that `9AD^(2)= 7AB^(2)`.
View SolutionIf A be the area of a right Deltaand b be one of the sides containing the right angle, prove that the length of the altitude on the hypotenuse is `(2Ab)/(sqrt(b^(4)+4A^(2))`.
View SolutionThe perimeter of a right triangle 60 cm. If its hypotenuse is 25 cm, find the area of the triangle.
View Solution
PRACTICE THOROUGHLY questions and complete solutions for chapter TRIANGLES of KUMAR PRAKASHAN of Class 10