Complete Solutions to exam of chapter mar 2019 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | mar 2019 |
| CAMBRIDGE PUBLICATION(KANNAD) | exam |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ nನೇ ಪದ `a_n` = 24 - 3n, ಆದಾಗ, ಆ ಶ್ರೇಢಿಯ 2ನೇ ಪದವು
View Solution2x + 3y - 9 = 0 ಮತ್ತು 4x + 6y - 18 = 0 ಸಮೀಕರಣಗಳನ್ನು ಪ್ರತಿನಿಧಿಸುವ ರೇಖೆಗಳು
View Solutionಒಂದು ವೃತ್ತದ ಎರಡು ಬಿಂದುಗಳ ಮೂಲಕ ಹಾದು ಹೋಗುವ ಸರಳರೇಖೆಯು
View Solutionಒಂದು ವೃತ್ತದ ವಿಸ್ತೀರ್ಣವು 49 `pi` ಚದರಮಾನಗಳು ಆದರೆ, ಅದರ ಪರಿಧಿಯು
View Solutionಎರಡು ಅನುಕ್ರಮ ಧನ ಪೂರ್ಣಾಂಕಗಳ ಗುಣಲಬ್ಧ 30. ಇದರ ಬೈಜಿಕ ರೂಪ...
View Solutionಯಾವುದೇ ಎರಡು ಧನ ಪೂರ್ಣಾಂಕ a ಮತ್ತು b ಗಳಿಗೆ ಮ.ಸಾ.ಅ (a, b) x ಲ.ಸಾ.ಅ (a, b) ಇದಕ್ಕೆ ಸಮನಾದದ್ದು.
View Solution
cos `48^@` - sin `42^@` ಯ ಬೆಲೆಯು
View SolutionP(A) = 0.05 ಆದರೆ, P`(overlineA)` ಯು
View Solution`17 =6 xx2 +5 `ಇದನ್ನು ಯೂಕ್ಷಿಡ್ ಭಾಗಾಕಾರ ಅನುಪ್ರಮೇಯ a = bq +r, ಗೆ ಹೋಲಿಸಿದಾಗ ಶೇಷವನ್ನು ಸೂಚಿಸುವ ಸಂಖ್ಯೆ ಯಾವುದು?
View SolutionP(x) = `x^2` - 3 ಬಹುಪದೋಕ್ತಿಯ ಶೂನ್ಯತೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
View SolutionP (x) = 2 `x^2` - `x^3` + 5 ಬಹುಪಡೋಕ್ತಿಯ ಮಹತ್ತಮ ಘಾತ (ಡಿಗ್ರಿ) ಬರೆಯಿರಿ.
View Solution2 `x^2` - 4x + 3 = 0 ವರ್ಗಾಸಮೀಕರಣದ ಶೋಧಕದ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ .
View Solutionಶಂಕುವಿನ ಭಿನ್ನಕದ ಪಾಶ್ಚ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯುವ ಸೂತ್ರವನ್ನು ಬರೆಯಿರಿ.
View Solution2 + 7 + 12........... ಈ ಸಮಾಂತರ ಶ್ರೇಣಿಯ ಮೊದಲ 20 ಪದಗಳ ಮೊತ್ತವನ್ನು ಸೂಕ್ತವಾದ ಸೂತ್ರದ ಸಹಾಯದಿಂದ ಕಂಡುಹಿಡಿದಿಠಿ.
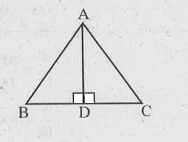
View Solution`triangle ABC` ಯಲ್ಲಿ `AD bot BC` ಮತ್ತು `AD^(2) = BD x CD` ಆಗಿದೆ. ಹಾಗಾದರೆ `AB^(2) + AC^(2) = (BD + CD)^(2)` ಎಂದು ಸಾಧಿಸಿ.
View Solutionಈ ಕೆಳಗಿನ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣ ಜೋಡಿಗಳನ್ನು ಸೂಕ್ತ ವಿಧಾನದಿಂದ ಬಿಡಿಸಿ :
x + y = 5, 2x – 3y = 5
View SolutionA (4, -3) ಮತ್ತು B (8, 5) ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖಾಖಂಡವನ್ನು ಆಂತರಿಕವಾಗಿ 3:1 ಅನುಪಾತದಲ್ಲಿ ವಿಭಾಗಿಸುವ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
View Solution`3 + sqrt5` ನ್ನು ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಎಂದು ಸಾಧಿಸಿ.
View Solution`P(x) = ax^(2) +bx +c` ವರ್ಗ ಬಹಪದೋಕ್ತಿಯ ಶೂನ್ಯಗಳ ಮೊತ್ತ -3 ಮತ್ತು ಗುಣಲಬ್ಧ 2 ಆದರೆ, b +c = 5a ಎಂದು ಸಾಧಿಸಿ.
View Solution`P(x) = 3x^(3) +x^(2) + 2x +5` ನ್ನು `g(x) =x^(2) + 2x+1` ರಿಂದ ಭಾಗಿಸಿದಾಗ ದೊರಕುವ ಭಾಗಲಬ್ಧ ಮತ್ತು ಶೇಷವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
View Solution`2x^2` - 5x + 3 = 0 ಸಮೀಕರಣವನ್ನು ಸೂತ್ರದ ಸಹಾಯದಿಂದ ಬಿಡಿಸಿ.
View Solutionಒಂದು ಆಯತಾಕಾರದ ಜಮೀನಿನಿ ಉದ್ದವು ಅದರ ಅಗಲದ ಮೂರಂಷ್ಟಿದೆ. ಜಮೀನಿನ ವಿಸ್ತೀರ್ಣವು 147 ಚದರ ಮೀಟರ್ಗಳಾದರೆ ಅದರ ಉದ್ದ ಮತ್ತು ಅಗಲವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
View Solution`sintheta =12/13` ಆದರೆ, cos`theta` ಮತ್ತು tan`theta` ಗಳ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
View Solution`sqrt3tantheta` = 1 ಮತ್ತು’`theta`’ ಲಘುಕೋನವಾದಾಗ `sin3theta` + `cos2theta` ಬೆಲೆ ಕಂಡುಹಿಡಿಯಿರಿ.
View Solution`[(1+costheta)/(1-costheta)]` =`(cosectheta + cottheta)^2` ಎಂದು ಸಾಧಿಸಿ.
View Solution1 ರಿಂದ 6ರವರೆಗಿನ ಸಂಖ್ಯೆಗಳನ್ನು ಹೊಂದಿರುವ ಒಂದು ಘನಾಕೃತಿಯ ದಾಳವನ್ನು ಒಂದು ಬಾರಿ ಉದರುಳಿಸಿದಾಗ, ಬೆಸ ಸಂಖ್ಯೆ ಮೇಲೆ ಬರುವ ಸಂಭವನೀಯತೆಯು,
View Solutionಶಂಕುವಿನ ಭಿನ್ನಕ ರೂಪದ ಕಸದ ಬುಟ್ಟಿಯ ವೃತ್ತಾಕಾರದ ಎರಡು ಬದಿಯ ತ್ರಿಜ್ಯಗಳು ಕ್ರಮವಾಗಿ 15cm ಮತ್ತು 8 cm ಆಗಿದೆ ಇದರ ಆಳವು 63 cm, ನಪ್ಪಿದ್ದರೆ, ಕಸದ ಬುಟ್ಟಿಯ ಘನಫಲವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
View Solutionಬಾಹ್ಯ ಬಿಂದುವಿನಿಂದ ವೃತ್ತಕ್ಕೆ ಎಳೆದ ಸ್ಪರ್ಶಕಗಳ ಉದ್ದವು ಸಮನಾಗಿರುತ್ತದೆ". ಎಂದು ಸಾಧಿಸಿ.
View Solutionಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಏಳನೇ ಪವು.ಅದರ ಎರಡನೇ ಪದದ ನಾಲ್ಕರಪ್ಪಿದೆ ಹಾಗೂ ಶ್ರೇಢಿಯ ಹನ್ನೇರಡನೇ ಪದವು ನಾಲ್ಕನೇ ಪದದ ಮೂರಂಷ್ಟಕ್ಕಿಂತ 2 ಹೆಚ್ಚಾಗಿದೆ. ಹಾಗಾದರೆ ಆ ಶ್ರೇಢಿಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
View Solutionಒಂದು ರೇಖಾಖಂಡವನ್ನು ಸಮಾಂತರ ಶ್ರೇಢಿಯಲ್ಲಿರುವಂತೆ ನಾಲ್ಕು ಭಾಗಗಳಾಗಿ ವಿಭಾಗಿಸಿದೆ. ಇವುಗಳಲ್ಲಿ ಮೂರನೇ ಮತ್ತು ನಾಲ್ಕನೇ ಭಾಗದ ಉದ್ದಗಳ ಮೊತ್ತವು ಮೊದಲೆರಡು ಭಾಗಗಳ ಉದ್ದಗಳ ಮೊತ್ತದ ಮೂರಂಷಪ್ಪಿದೆ. ನಾಲ್ಕನೇ ಭಾಗದ ಉದ್ದವು 14 ಸೆಂ.ಮೀ.ಗಳಾದರೆ. ಆ ರೇಖಾ ಖಂಡದ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
View SolutionA (-3, 2), B(-1, -4) ಮತ್ತು C(5, 2) `triangle`ABC ಯು ಶೃ೦ಗ ಬಿಂದುಗಳಾಗಿವೆ. M ಮತ್ತು N ಗಳು ಕ್ರಮವಾಗಿ AB ಮತ್ತು AC ಗಳ ಮಧ್ಯಬಿಂದುಗಳಾದರೆ 2 MN= BC ಎಂದು ಸಾಧಿಸಿ.
View SolutionA(-5, -1) B(3, -5) ಮತ್ತು C(5, 2) ಶೃಂಗ ಬಿಂದುಗಳನ್ನು ಹೊಂದಿರುವ ತ್ರಿಭುಜದ ವಿಸ್ತೀರ್ಣವು ಅದೇ ABC ತ್ರಿಭುಜದ ಬಾಹುಗಳ ಮಧ್ಯಬಿಂದುಗಳನ್ನು ಸೇರಿಸಿದಾಗ ಉಂಟಾದ ತ್ರಿಭುಜದ ವಿಸ್ತೀರ್ಣದ ನಾಲ್ಕರಷ್ಟಿದೆ ಎಂದು ಸಾಧಿಸಿ .
View Solutionಗೋಪುರವೊಂದರ ಪಾದದಿಂದ 4m ಮತ್ತು 9m ದೂರದಲ್ಲಿ ಒಂದೇ ಸರಳರೇಖೆಯ ಮೇಲಿನ ಬಿಂದುಗಳ ಮೇಲಿನ ಬಿಂದುವಿನಿಂದ ಗೋಪುರದ ಮೇಲ್ತುದಿಗೆ ಉನ್ನತ ಕೋನಗಳು ಪರಸ್ಪರ ಪೂರಕಗಳಾಗಿವೆ. ಗೋಪುರದ ಎತ್ತರವು 6m ಎಂದು ಸಾಧಿಸಿ.
View Solution14 cm ತ್ರಿಜ್ಯವಿರುವ ಇರುವ ಒಂದು ಅರ್ಧಗೋಳಾಕೃತಿಯ ಪಾತ್ರೆಯಲ್ಲಿ ಪೂರ್ಣವಾಗಿ ಮರಳನ್ನು ತುಂಬಿದೆ. ಈ ಮರಳನ್ನು ಸಮತಟ್ಟಾದ ನೆಲದ ಮೇಲೆ ಸುರಿದಾಗ ಆ ಮರಳಿನ ರಾಶಿಯು ಶಂಕುವಿನ ಆಕೃತಿಯಾಗುತ್ತದೆ. ಈ ಶಂಕು ಆಕೃತಿಯ ಮರಳಿನ ರಾಶಿಯ ಎತ್ತರವು 7cm. ಆದಾಗ ಶಂಕುವಿನ ವೃತ್ತ ಪಾದವು ನೆಲದ ಮೇಲಿನ ಎಷ್ಟು ವಿಸ್ತೀರ್ಣವನ್ನು ಆಕ್ರಮಿಸಿಕೊಳ್ಳುತ್ತದೆ ಎಂಬುದನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
View Solution'ಎರಡು ಸಮರೂಪ ತ್ರಿಭುಜಗಳ ವಿಸ್ತೀರ್ಣಗಳ ಅನುಪಾತವು ಅವುಗಳ ಅನುರೂಪ ಬಾಹುಗಳ ವರ್ಗಗಳ ಅನುಪಾತಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ'' . ಎಂದು ಸಾಧಿಸಿ.
View Solution
exam questions and complete solutions for chapter mar 2019 of CAMBRIDGE MATHS (KANNADA) of Class 10