There is a point inside a circle. What is the probability that this point is close to the circumference than to the centre ?
3/4
1/2
1/4
1/3
The correct Answer is:A
To solve the problem of finding the probability that a point inside a circle is closer to the circumference than to the center, we can follow these steps:
Step 1: Understand the Problem
We need to find the area where points are closer to the circumference than to the center of the circle.
Step 2: Define the Circle
Let the radius of the circle be r. The center of the circle is point O and the circumference is at a distance r from O.
Step 3: Determine the Distance Criteria
A point P inside the circle is closer to the circumference than to the center if the distance from P to the circumference is less than the distance from P to the center.
Step 4: Set Up the Inequality
If the distance from point P to the center O is d, then the distance from P to the circumference is r−d. We need to find when:
r−d<d
This simplifies to:
r<2d⇒d>r2
Step 5: Identify the Relevant Area
The points that satisfy d>r2 lie outside a smaller circle with radius r2 centered at O.
Step 6: Calculate Areas
1. Area of the larger circle (radius r):
Alarge=πr2
2. Area of the smaller circle (radius r2):
Asmall=π(r2)2=πr24
3. Area of the annular region (the area between the two circles):
Aannulus=Alarge−Asmall=πr2−πr24=πr2(1−14)=πr234
Step 7: Calculate the Probability
The probability that a randomly chosen point inside the circle is closer to the circumference than to the center is given by the ratio of the area of the annular region to the area of the larger circle:
P=AannulusAlarge=3πr24πr2=34
Conclusion
Thus, the required probability is:
34
---
We need to find the area where points are closer to the circumference than to the center of the circle.
Let the radius of the circle be r. The center of the circle is point O and the circumference is at a distance r from O.
A point P inside the circle is closer to the circumference than to the center if the distance from P to the circumference is less than the distance from P to the center.
If the distance from point P to the center O is d, then the distance from P to the circumference is r−d. We need to find when:
r−d<d
This simplifies to:
r<2d⇒d>r2
The points that satisfy d>r2 lie outside a smaller circle with radius r2 centered at O.
1. Area of the larger circle (radius r):
Alarge=πr2
Asmall=π(r2)2=πr24
Aannulus=Alarge−Asmall=πr2−πr24=πr2(1−14)=πr234
The probability that a randomly chosen point inside the circle is closer to the circumference than to the center is given by the ratio of the area of the annular region to the area of the larger circle:
P=AannulusAlarge=3πr24πr2=34
Thus, the required probability is:
34
Topper's Solved these Questions
- POLYNOMIAL,QUADRATIC EQUATION & INEQUALITIESBook:NDA PREVIOUS YEARSChapter:POLYNOMIAL,QUADRATIC EQUATION & INEQUALITIESExercise:Math
Explore 170 Videos
- PROPERTIES OF TRIANGLE, INVERSE TRIGONOMETRIC FUNCTIONBook:NDA PREVIOUS YEARSChapter:PROPERTIES OF TRIANGLE, INVERSE TRIGONOMETRIC FUNCTIONExercise:MCQ
Explore 103 Videos
Similar Questions
A point is chosen at random inside a circle. Find the probability that the point is closer to the centre of the circle than to its circumference.
View SolutionA point is selected at random from the interior of a circle. The probability that the point is closer to the centre than the boundary of the circle is
View Solution
Knowledge Check
There is a point inside a circle. What is the probability that this point is close to the circumference than to the center?
AA. 34BB. 12CC. 14DD. 13A point is selected at random from inside a circle. The probability that the point is closer to the circumference of the circle than to its centre, is
A23B13C34D14A point is chosen at random inside a circle. What is the probability that the point is closer to the centre of the circle than to its boundary?
A1√2B14C13D12
A square is incribed in a circle . If p1 is the probability that a randomly chosen point of the circle lies within the square and p2 is the probability that the point lies outside the square then
View SolutionA square is inscribed in a circle. If pr is the probability that a randomly chosen point inside the circle lies within the square and p, is the probability that the point lies outside the square, then
View SolutionThere is a point inside a circle. What is the probability that this point is close to the circumference than to the center?
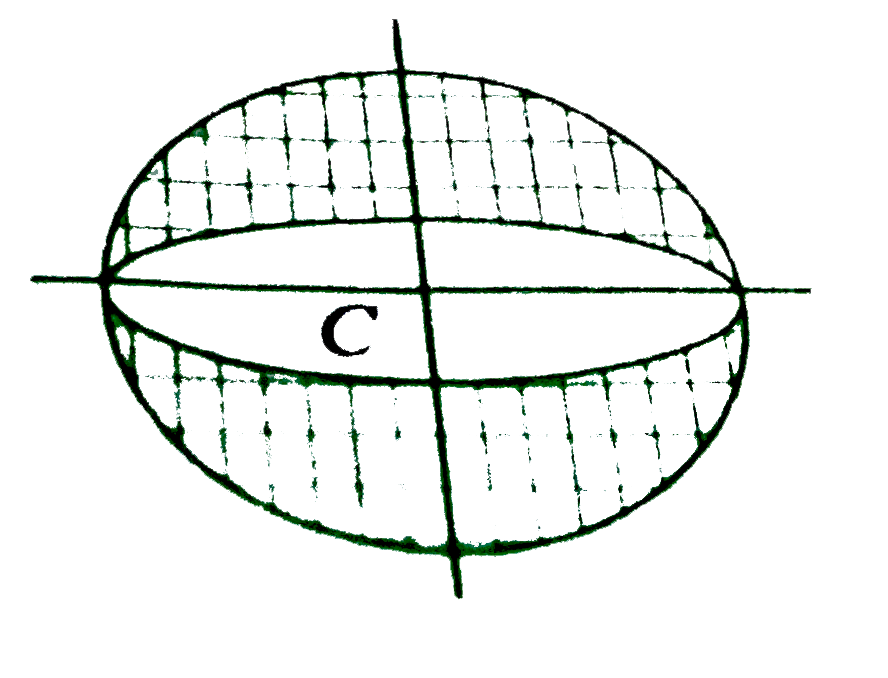
View SolutionThere are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity 2√2/3 is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
1−b2a2=89orb2a2=19
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
p=Area of shaded regionArea of circle
=πa2−πabπa2=1−ba=1−13=23
Now, answer the following questions.
A point is selected at random inside a circle. The probability that the point is closer to the center of the circle than to its circumference is
View SolutionA point is selected randomly from the interior of a circle. The probability that the point is closer to the centre, then the boundary of circle is
View Solution