Explain the use of a metre bridge for finding unknown resistance.
It works bridge is balanced, we get PQ=RS.
it consists of uniform wire AC one metre long, soldered to the ends of two thick rectangular strips of copper A and C on the wooden base. A metre scale is also fitted on the wooden board. Another copper strip D is also fixed on the wooden board as shown in the figure. R is a resistance box and S is unknown resistance. positive of battery is connected to point A and negative to point C. A sliding contact B called jockey can be moved along the graduated scale. G is a galvanometer connected between D and B.
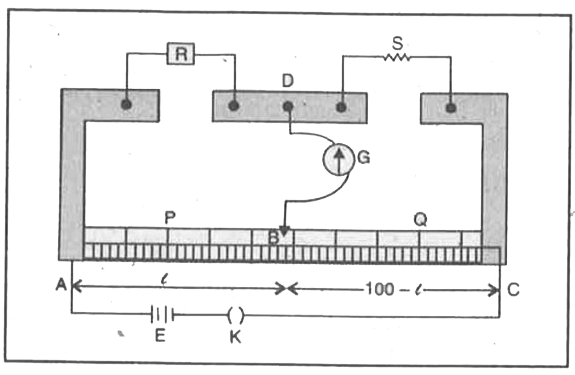
Key K is inserted and a known resistance R is taken out from the resistance box. move the jockey on the wire till for a certain position B, galvanometer shows no deflection. the bridge is then said to be balanced. if P(=lr) and Q[(=(100-l)r] are the resistance of part AB and BC, then we have
PQ=RS
or RS=PQ=lr(100−l)l
or RS=lr100−l
or S=100−llR
Knowing l, and R, S can be calculated.
Topper's Solved these Questions
- BOOK - MBD -HARYANA BOARDCHAPTER - CURRENT ELECTRICITYEXERCISE - OBJECTIVE TYPE QUESTIONS20videos
CURRENT ELECTRICITY
- BOOK - MBD -HARYANA BOARDCHAPTER - CURRENT ELECTRICITYEXERCISE - SHORT ANSWER TYPE QUESTIONS9videos
CURRENT ELECTRICITY
- BOOK - MBD -HARYANA BOARDCHAPTER - BOARD QUESTION PAPER (SOLVED) - 2019EXERCISE - LONG ANSWER TYPE QUESTIONS4videos
BOARD QUESTION PAPER (SOLVED) - 2019
- BOOK - MBD -HARYANA BOARDCHAPTER - DUAL NATURE OF MATTER AND RADIATIONSEXERCISE - OBJECTIVE TYPE QUESTIONS17videos
DUAL NATURE OF MATTER AND RADIATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
During an experiment with a metre bridge, the galvanometer shows a null point when the jockey is pressed at 40.0cm using a standard resistance of 90Ω, as shown in the figure. The least count of the scale used in the metre bridge is 1mm. The unknown resistance is
 A60±0.15ΩB135±0.56ΩC60±0.25ΩD135±0.23Ω
A60±0.15ΩB135±0.56ΩC60±0.25ΩD135±0.23Ω - Question 2 - Select One
Consider a metre bridge whose length of wire is 2m. A resistance of 10Ω is connected across one gap of the meter bridge and an unknown resistance is connected across the other gap. When these resistances are interchanged, the balance point shifts by 50 cm. What is the value of the unknown resistance?
A250ΩB10ΩC16.7ΩDNone of the above - Question 3 - Select One
In a metre bridge , the balancing length from the left end is found to be 40cm, when a known resistance of 3Ω is placed in the right gap, then the value of unknown resistance is
A1ΩB2ΩC3ΩD4Ω
Draw the circuit diagram to determine unknown resistance using meter bridge. Write the equation used for determining the unknown resistance.
View SolutionAn unknown resistance 'X' is placed in the left gap and and a known resistance of 60Ω is plaecd in the right gap of metre bridge. The null point is obtained at 40 cm from the left end fo the bridge. Fid the unknown resistance.
View SolutionPotentiometer and metre bridge
View SolutionTwo equal resistance are connected in the gaps of a metre bridge. If the resistance in the left gap is increased by 10% the balancing point shift
View SolutionTwo equal resistance are connected in the gaps of a metre bridge. If the resistance in the left gap is increased by 10% the balancing point shift
View Solution
