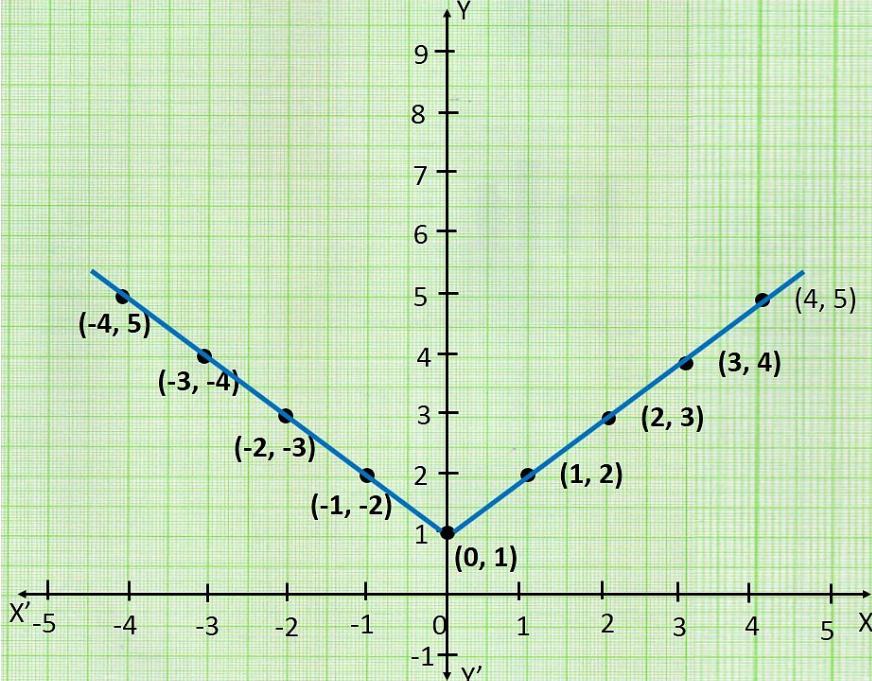
The function f is defined by f(x)=⎧⎪⎨⎪⎩1−x x<01 x=0x+1 x>0⎫⎪⎬⎪⎭. Draw the graph of f(x).
Video Solution
Text Solution
f(x)=⎧⎪⎨⎪⎩1−x x<01 x=0x+1 x>0⎫⎪⎬⎪⎭
Let f(x)=y.Then,
y=1−x or x+y=1 forx<0
y=1 forx=1
andy=x+1 or −x+y=1 for x>0
To draw the graph of f(x),draw the line x+y=1 and take that part for which x<0
i.e., take that portion of the line which lies on the left side of the y−axis.
For x>0, draw the line −x+y=1 and take that portion that lies on the right side of the y−axis.
Forx=0,mark the point (0,1).
So, the graph of f(x) is as shown in Figure
|
Updated on:21/07/2023
Related Playlists
- BOOK - NCERTCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE12videos
RELATIONS AND FUNCTIONS
- BOOK - NCERTCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2.35videos
RELATIONS AND FUNCTIONS
- BOOK - NCERTCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2.110videos
RELATIONS AND FUNCTIONS
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - EXERCISE 16.321videos
PROBABILITY
- BOOK - NCERTCHAPTER - SEQUENCES AND SERIESEXERCISE - EXERCISE 9.56videos
SEQUENCES AND SERIES
Similar Practice Problems
- Question 1 - Select One
Let f:R→R be a function defined by f(x)=|x|3+|x|1+x2, then the graph of f(x) lies in the
AI and II quadrantsBI and III quadrantsCII and III quadrantsDIII and IV quadrants . - Question 1 - Select One
A function f defined by f(x)=In(√x2+1−x) is
Aan even functionBan odd functionCBoth even and odd functionDNeither even nor odd function - Question 1 - Select One
If f(x) is a real-valued function defined as f(x)=In(1−sinx), then the graph of f(x) is
Asymmetric about the line x=πBsymmetric about the y-axisCsymmetric and the line x=π2Dsymmetric about the origin - Question 1 - Select One
Let a function f be defined by f(x)=x-|x|x for x≠0 and f(0)=2. Then f is
Acontinuous nowhereBcontinuous everywhereCcontinuous for all x except x =1Dcontinuous for all x except x=0 - Question 1 - Select One
The function f defined as f(x)=(sinx2)/x for x≠0 and f(0)=0 is:
Acontinuous and derivable at x = 0,Bneither continuous nor derivable at x = 0,Ccontinuous but not derivable at x = 0Dnone of these. - Question 1 - Select One
If the function,f:[1,∞]→[1,∞] is defined by f(x)=3x(x−1), then f−1(x) is
A(12)x(x−1)B12(1+√1+4log2x)C12(1−√1+4log2x)Dnot defined
Similar Questions
The function f is defined by f(x)=⎧⎪⎨⎪⎩1−x x<01 x=0x+1 x>0⎫⎪⎬⎪⎭. Draw the graph of f(x).
View SolutionIf a function f(x) is defined as f(x)={−x,x<0,x2,0≤x≤tandx2−x+1,x>1 then
View SolutionIf f(x) is a real valued function defined as f(x)=In(1−sinx) then graph of f(x) is
View SolutionA function f is defined by f(x) =x2+1. Find f(0), f(5), f(10).
View Solution

