AREAS OF PARALLELOGRAMS AND TRIANGLES for Class 9 MATHS
INTRODUCTION
Toh bachcho humne abhi tak padha hai about the Geometry jo ki kisi bhi cheez ki measurement ke liye use kiya jata hai like earth, lands aur fields ki dimension ko measure karne se bana hai . For example ek farmer ko apne 3 bachoo mei ek triangular field ko divide krna hai . Toh usne uss triangle ki ek side ko 3 equal parts mei divide kiya aur unn 2 points ko opposite vertex se jod diya . Kya lagta hai aapko ki ye division equal hai ya nhi ? Iska jawab jaane ke liye aapko area of plane figures recall karna hoga.
Toh chaliye aise hi kuch aur interesting facts janne ke liye ab hum padhte hai kuch aur figures ke area ke baare mein.
INTRODUCTION
Toh bachcho humne abhi tak padha hai about the Geometry jo ki kisi bhi cheez ki measurement ke liye use kiya jata hai like earth, lands aur fields ki dimension ko measure karne se bana hai . For example ek farmer ko apne 3 bachoo mei ek triangular field ko divide krna hai . Toh usne uss triangle ki ek side ko 3 equal parts mei divide kiya aur unn 2 points ko opposite vertex se jod diya . Kya lagta hai aapko ki ye division equal hai ya nhi ? Iska jawab jaane ke liye aapko area of plane figures recall karna hoga.
Toh chaliye aise hi kuch aur interesting facts janne ke liye ab hum padhte hai kuch aur figures ke area ke baare mein.
INTRODUCTION
Baccho aapne apni previous classes m geometry k baare m aur geometry se related bohot se topics cover kiye hai. Hum sab jaante hai ki geometry humari life m ek bohot hi important role play krta hai. Structures of almost everything around us is derived from a geometrical concept. A very important application of geometry is finding out areas of different planes. Baccho iss chapter m hum area se related concepts cover krenge related to parallelograms and triangles. Baccho, aapne congruency k baare m previous classes m pdha hai. We know that congruent figures are equal in area, shape and size.We will use congruency rules to prove theorems as we proceed with the chapter. So let's begin!
INDEX
Figures on the Same Base and Between the Same Parallels|Parallelograms on the same Base and Between the same Parallels|Triangles on the same Base and between the same Parallels|Summary
INDEX
Figures on the Same Base and Between the Same Parallels|Parallelograms on the same Base and Between the same Parallels|Triangles on the same Base and between the same Parallels|Summary
CONCEPT OF AREA
The plane enclosed by a simple closed figure is
called a planar region corresponding to that figure . The magnitude or measure of this planar region is called its AREA
CONCEPT OF AREA
The plane enclosed by a simple closed figure is
called a planar region corresponding to that figure . The magnitude or measure of this planar region is called its AREA
Explanation
Bachcho triangles aapke liye kuch new topic nahi hai ye aap apni previous classes mai bhi padh chuke ho lekin class 9th mai aap triangles aur ache aur meaningful way mai padhoge aur wo bhi bahot interesting examples ke sath to chaliye padhte hain.
Explanation
Bachcho triangles aapke liye kuch new topic nahi hai ye aap apni previous classes mai bhi padh chuke ho lekin class 9th mai aap triangles aur ache aur meaningful way mai padhoge aur wo bhi bahot interesting examples ke sath to chaliye padhte hain.
FIGURES ON THE SAME BASE AND BETWEEN SAME PARALLELS
Baccho, aap sabne apni previous classes m parallel lines aur unse related properties k baare m pdha hai. Iss section m hum ye jaanenge ki hum kaise conclude kr skte hai ki do figures same base p aur same parallel k beech m lie krrhe hai. For this, observe the sides and vertices of the following figures:
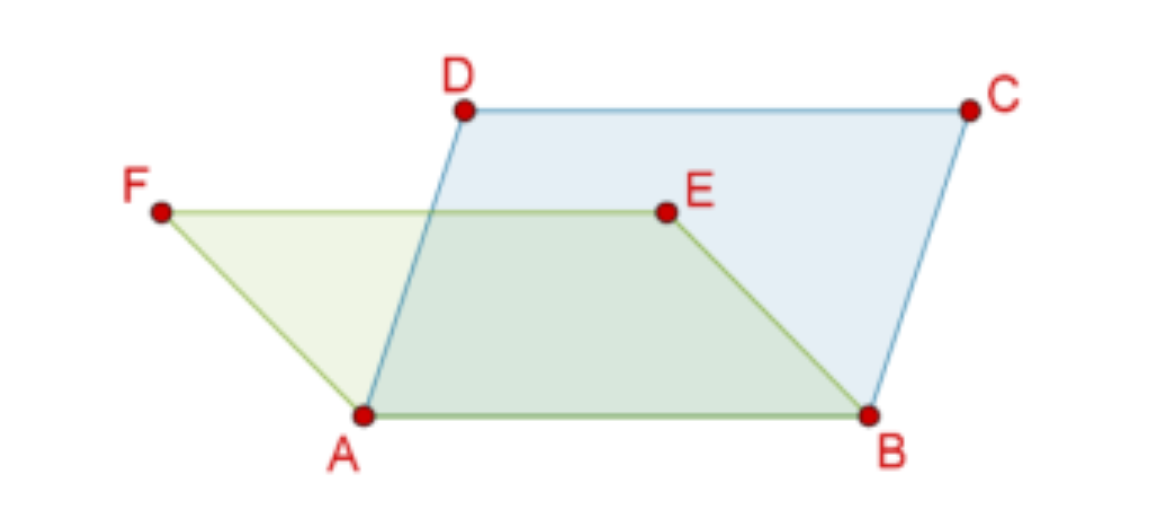
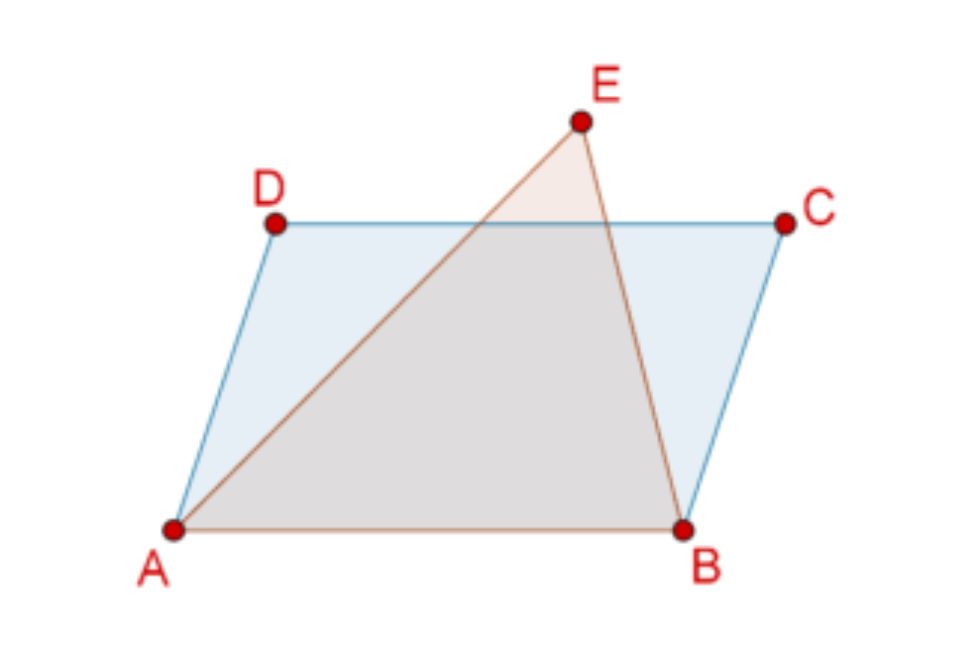
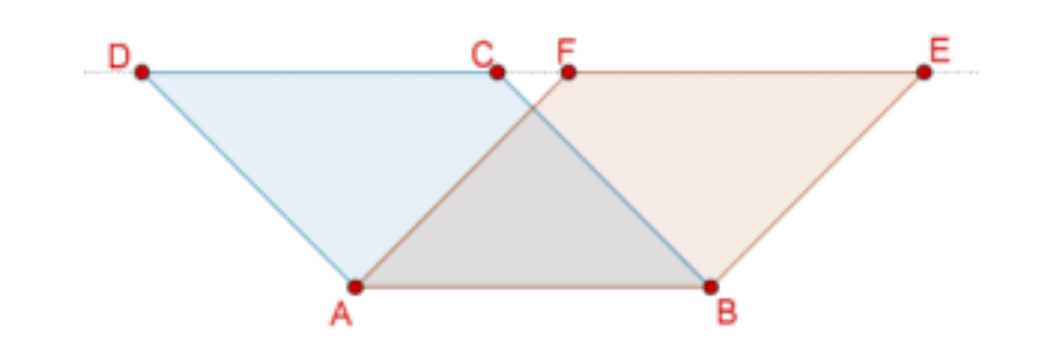

Baccho, after observing the above figures, we can see that two figures can be said to be on the same base and between the same parallels if they have a common base (a common side) and the vertex (or vertices) opposite to the common base of each figure lie on some line parallel to the base.
FIGURES ON THE SAME BASE AND BETWEEN SAME PARALLELS
Baccho, aap sabne apni previous classes m parallel lines aur unse related properties k baare m pdha hai. Iss section m hum ye jaanenge ki hum kaise conclude kr skte hai ki do figures same base p aur same parallel k beech m lie krrhe hai. For this, observe the sides and vertices of the following figures:




Baccho, after observing the above figures, we can see that two figures can be said to be on the same base and between the same parallels if they have a common base (a common side) and the vertex (or vertices) opposite to the common base of each figure lie on some line parallel to the base.
FIGURES ON THE SAME BASE AND BETWEEN SAME PARALLELS
Baccho, aap sabne apni previous classes m parallel lines aur unse related properties k baare m pdha hai. Iss section m hum ye jaanenge ki hum kaise conclude kr skte hai ki do figures same base p aur same parallel k beech m lie krrhe hai. For this, observe the sides and vertices of the following figures:




Baccho, after observing the above figures, we can see that two figures can be said to be on the same base and between the same parallels if they have a common base (a common side) and the vertex (or vertices) opposite to the common base of each figure lie on some line parallel to the base.
PARALLELOGRAMS ON THE SAME BASE AND BETWEEN SAME PARALLELS
Baccho, ab hum dekhenge ki agar do parallelograms same base aur same parallels k beech m lie krte hai, to hume kya relations milte hai.
Jab do parallelograms sabe base aur same parallels k beech m lie krte hai to unke areas same hojate hai. Observe the following figures and try to measure the areas of the given parallelograms visually: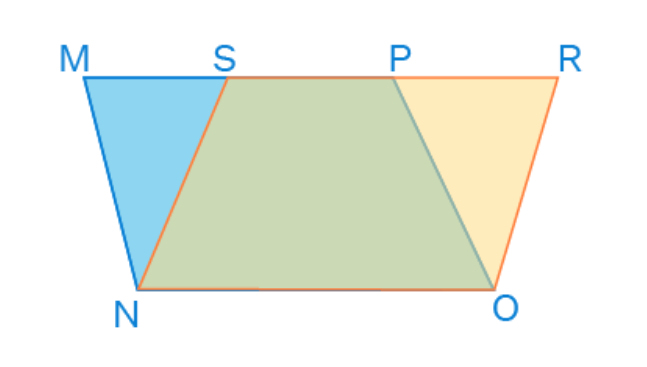

Baccho, ab hum iss theorem ka mathematical proof dekhenge.
PARALLELOGRAMS ON THE SAME BASE AND BETWEEN SAME PARALLELS
Baccho, ab hum dekhenge ki agar do parallelograms same base aur same parallels k beech m lie krte hai, to hume kya relations milte hai.
Jab do parallelograms sabe base aur same parallels k beech m lie krte hai to unke areas same hojate hai. Observe the following figures and try to measure the areas of the given parallelograms visually:


Baccho, ab hum iss theorem ka mathematical proof dekhenge. We will also see if the reverse of this theorem holds true or not.
PARALLELOGRAMS ON THE SAME BASE AND BETWEEN SAME PARALLELS
Baccho, ab hum dekhenge ki agar do parallelograms same base aur same parallels k beech m lie krte hai, to hume kya relations milte hai.
Jab do parallelograms sabe base aur same parallels k beech m lie krte hai to unke areas same hojate hai. Observe the following figures and try to measure the areas of the given parallelograms visually:


Baccho, ab hum iss theorem ka mathematical proof dekhenge. We will also see if the reverse of this theorem holds true or not.
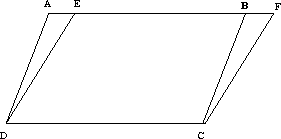
Theorem 9.1
Parallelograms on the same base and between the same parallels are equal in area.
Two parallelograms ABCE and ABDF, on
the same base AB and between the same parallels AB and CF are given.
To prove , ar (ABCE) = ar (ABDF).
Can you see that △BCD and △AEF might be congruent? This is easy to show. We have:
BC=AE (opposite sides of a parallelogram are equal)
∠BCD=∠AEF (corresponding angles when BC∣∣AEand CE is the transversal)
∠BDC=∠AFE (corresponding angles when BD∣∣AF and FD is the transversal)
By the ASA criterion, the two triangles are congruent, which means that their areas are equal. It can be written as area (BCD) = area (AEF). Now, if we add the area of the region ABDE, we will get,
area (BCD) + area (ABDE) = area (AEF) + area (ABDE)
area(ABCE) = area(ABDF)
Hence, it is proved that the two parallelograms drawn on the same base and between the same parallels are equal in area.
The converse of this theorem also holds true, which implies, Parallelograms on the same base (or equal bases) and having equal areas lie between the same parallels
Theorem 9.1 :
Parallelograms on the same base and between the same parallels are equal in area.

Two parallelograms ABCE and ABDF, on
the same base AB and between the same parallels AB and CF are given.
. To prove , ar (ABCE) = ar (ABDF).
Can you see that △BCD and △AEF might be congruent? This is easy to show. We have:
BC=AE (opposite sides of a parallelogram are equal)
∠BCD=∠AEF (corresponding angles when BC∣∣AEand CE is the transversal)
∠BDC=∠AFE (corresponding angles when BD∣∣AF and FD is the transversal)
By the ASA criterion, the two triangles are congruent, which means that their areas are equal. It can be written as area (BCD) = area (AEF). Now, if we add the area of the region ABDE, we will get,
area (BCD) + area (ABDE) = area (AEF) + area (ABDE)
area(ABCE) = area(ABDF)
Hence, it is proved that the two parallelograms drawn on the same base and between the same parallels are equal in area.
Theorem 9.1 :
Parallelograms on the same base and between the same parallels are equal in area.

Two parallelograms ABCE and ABDF, on
the same base AB and between the same parallels AB and CF are given.
. To prove , ar (ABCE) = ar (ABDF).
Can you see that △BCD and △AEF might be congruent? This is easy to show. We have:
BC=AE (opposite sides of a parallelogram are equal)
∠BCD=∠AEF (corresponding angles when BC∣∣AEand CE is the transversal)
∠BDC=∠AFE (corresponding angles when BD∣∣AF and FD is the transversal)
By the ASA criterion, the two triangles are congruent, which means that their areas are equal. It can be written as area (BCD) = area (AEF). Now, if we add the area of the region ABDE, we will get,
area (BCD) + area (ABDE) = area (AEF) + area (ABDE)
area(ABCE) = area(ABDF)
Hence, it is proved that the two parallelograms drawn on the same base and between the same parallels are equal in area.
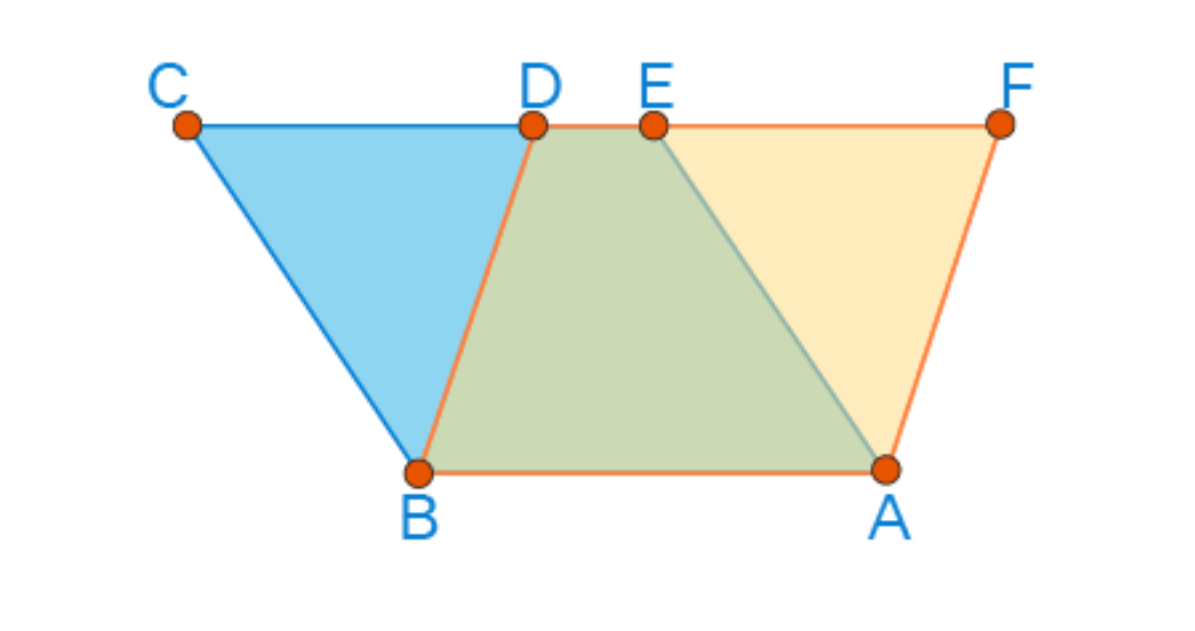
Derivation from Theorem 9.1 Triangle and a parallelogram on the same base and between same parallels
From the above proven theorem, we can also derive another theorem which states that If a triangle and parallelogram are on the same base and have the same altitude, the area of the triangle will be half that of the parallelogram. If they have same altitude, they will lie between the same parallels. Hence the area of the triangle will be equal to half that of the parallelogram.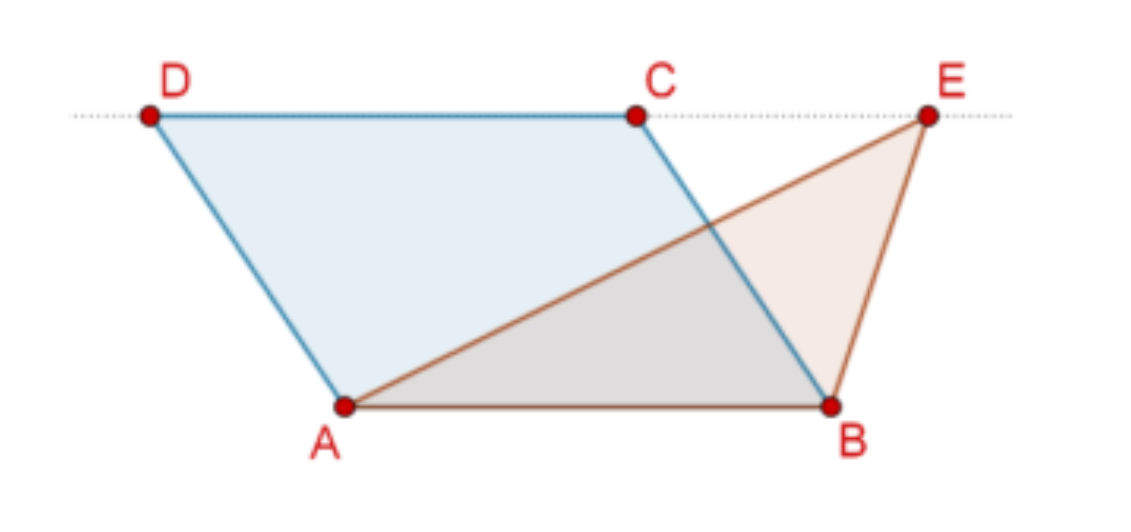
TRIANGLES ON THE SAME BASE AND BETWEEN THE SAME PARALLELS
Iss figure mai aapko two triangles dekhne ko milenge ABC and PBC aur inn dono ka base BC same hai aur inki parallel bhi equal hai BC and AP. What can you say
about the areas of such triangles? To answer this
question, hume ek activity perform karni hogi hume ek drawing sheet par bahot sare triangles ke pair banane honge aur jinka base aur parallel lines same ho and find their areas by the method of counting the squares. Each time jab triangles ka area find out karoge to aapko dekhne ko milega ki two triangles ka area (approximately) equal hoga. Aur isko aur ache se samajhne ke liye hum theorems and kuch interesting examples dekhenge.
TRIANGLES ON THE SAME BASE AND BETWEEN THE SAME PARALLELS

Iss figure mai aapko two triangles dekhne ko milenge ABC and PBC aur inn dono ka base BC same hai aur inki parallel bhi equal hai BC and AP. What can you say
about the areas of such triangles? To answer this
question, hume ek activity perform karni hogi hume ek drawing sheet par bahot sare triangles ke pair banane honge aur jinka base aur parallel lines same ho and find their areas by the method of counting the squares. Each time jab triangles ka area find out karoge to aapko dekhne ko milega ki two triangles ka area (approximately) equal hoga. Aur isko aur ache se samajhne ke liye hum theorems and kuch interesting examples dekhenge.
Example 1
ABCD is a parallelogram, AE⊥DCand CF⊥AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
AD=BC
AB=DC
In ABXE
EC∣∣AB (area of parallelogram)
DC∣∣AB
Area of AXBE=160cm2
From theorem 9.1
area(AXBE)=area(ABCD)=160cm2
FBYC is a rectangle
Area(FBYC)=x×10cm2
Area(FBYC)= 144cm2
x×10=144
x=14.4cm
BC=AD=14.4cm.
Example 1
ABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).

Given : A △ABC in which D is the midpoint of BC and E is the important of AD.
To PROVE : ar(△BED)=14ar(△ABC).
Proof : D is the midpoint of BC ⇒ AD is a median of △ ABC
⇒ar(△ABD=ar(△ACD)
[∴ a median divides a △ into two △ of equal area].
⇒ar(△ABD)=12ar(△ABC). ...(i)
E is the midpoint of AD ⇒ BE is a median of △ ABD
⇒ar(△BED)=ar(△BEA)
[∴ a median divides a △ into two △ of equal area].
⇒ar(△BED)=12ar(△ABD)=12{12ar(△ABC)} [using (i)]
⇒ar(△BED)=14ar(△ABC).
Example 1
ABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).

Given : - A △ABC in which D is the midpoint of BC and E is the important of AD.
To PROVE : ar(△BED)=14ar(△ABC).
Proof : D is the midpoint of BC ⇒ AD is a median of △ ABC
⇒ar(△ABD=ar(△ACD)
[∴ a median divides a △ into two △ of equal area].
⇒ar(△ABD)=12ar(△ABC). ...(i)
E is the midpoint of AD ⇒ BE is a median of △ ABD
⇒ar(△BED)=ar(△BEA)
[∴ a median divides a △ into two △ of equal area].
⇒ar(△BED)=12ar(△ABD)=12{12ar(△ABC)} [using (i)]
⇒ar(△BED)=14ar(△ABC).
Example 2
ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that:
(i) ar (ABCD) = ar (EFCD)
(ii) ar (ABCD) = DC × AL
As per the given figure, both ABCD and EFCD lies on the same parallel line EB and have common base CD.
We know, if two parallelograms lie on the same parallel line and have a common base, then they have equal area.
Thus, ar(ABCD)=ar(EFCD)
Also, we can say that ,
ar(ABCD)=ar(EFCD)=DC×DE
As, AL is a perpendicular to CD in rectangle EFCD,
AL=DE
So, ar(ABCD)=DC×AL
Example 2
If the medians of a △ABC intersect at G, show that
ar(△AGB)=ar(△AGC)=ar(△BGC)
=13ar(△ABC).
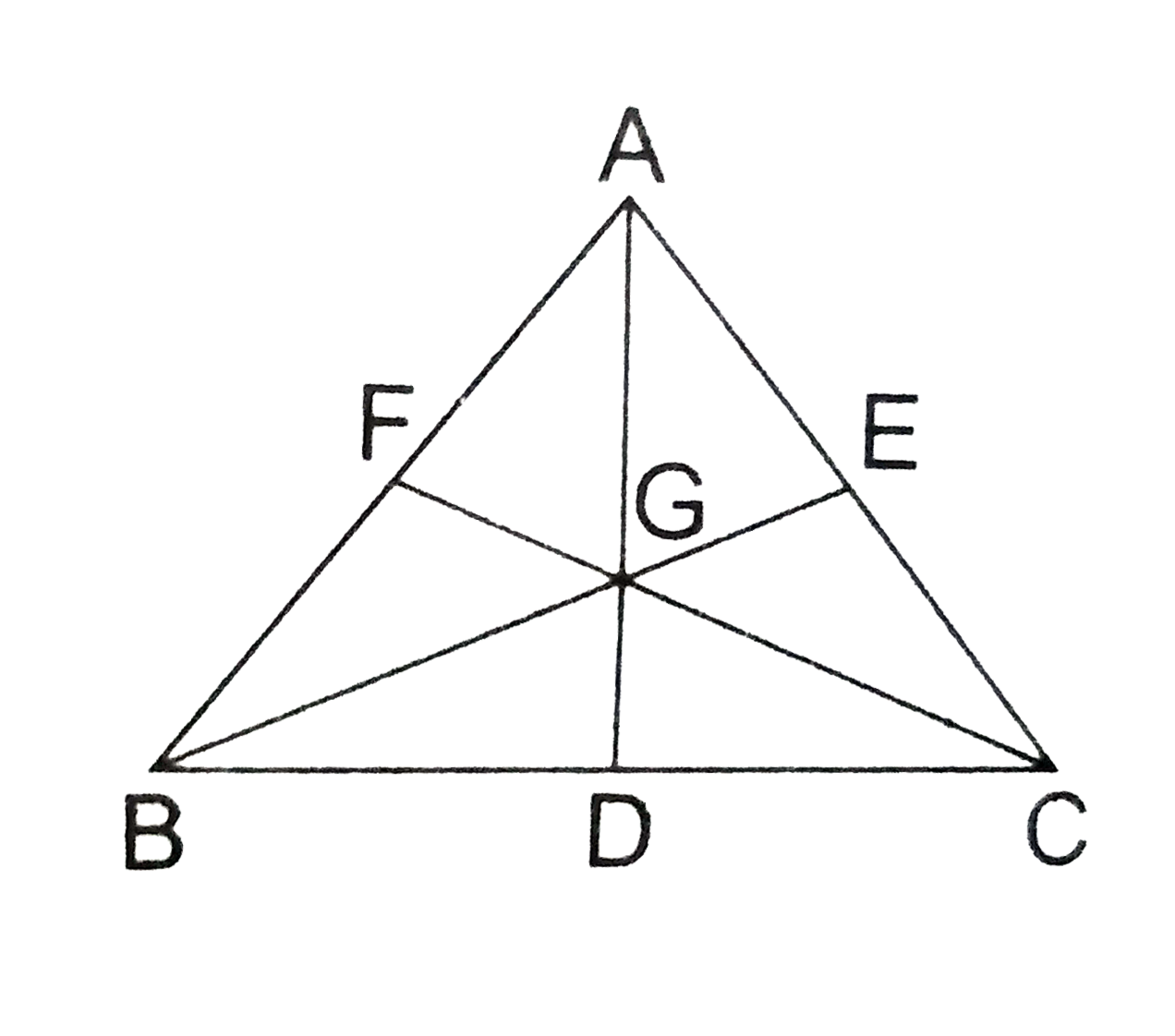
GIVEN A △ABC. Its medians AD, BE and CF intersect at G.
TO PROVE ar(△AGB)=ar(△AGC)=ar(△BGC)=13ar(△ABC)
PROOF We know that a median of a triangle divides it into two triangle of equal area.
In △ABC,AD is the median.
∴ar(△ABD)=ar(△ACD). ...(i)
In △GBC, GD is the median.
∴ar(△GBD)=ar(△GCD). ...(ii)
From (i) and (ii), we get
ar(△ABD)−ar(△GBD)=ar(△ACD)−ar(△GCD)
⇒ar(△AGB)=ar(△AGC).
Similarly, ar(△AGB)=ar(△BGC).
⇒ar(△AGB)=ar(△AGC).
But, ar(△ABC)=ar(△AGB)+ar(△AGC)+ar(△BGC)
=3ar(△AGB) [using (iii)].
∴ar(△AGB)=13ar(△ABC).
Hence, ar(△AGB)=ar(△AGC)=ar(△BGC)=13ar(△ABC).
Example 2
If the medians of a △ABC intersect at G, show that
ar(△AGB)=ar(△AGC)=ar(△BGC)
=13ar(△ABC).

GIVEN : - A △ABC. Its medians AD, BE and CF intersect at G.
TO PROVE ar(△AGB)=ar(△AGC)=ar(△BGC)=13ar(△ABC)
PROOF We know that a median of a triangle divides it into two triangle of equal area.
In △ABC,AD is the median.
∴ar(△ABD)=ar(△ACD). ...(i)
In △GBC, GD is the median.
∴ar(△GBD)=ar(△GCD). ...(ii)
From (i) and (ii), we get
ar(△ABD)−ar(△GBD)=ar(△ACD)−ar(△GCD)
⇒ar(△AGB)=ar(△AGC).
Similarly, ar(△AGB)=ar(△BGC).
⇒ar(△AGB)=ar(△AGC).
But, ar(△ABC)=ar(△AGB)+ar(△AGC)+ar(△BGC)
=3ar(△AGB) [using (iii)].
∴ar(△AGB)=13ar(△ABC).
Hence, ar(△AGB)=ar(△AGC)=ar(△BGC)=13ar(△ABC).
TRIANGLES ON THE SAME BASE AND BETWEEN THE SAME PARALLELS
Iss figure mai aapko two triangles dekhne ko milenge ABC and PBC aur inn dono ka base BC same hai aur inki parallel bhi equal hai BC and AP. What can you say
about the areas of such triangles? To answer this
question, hume ek activity perform karni hogi hume ek drawing sheet par bahot sare triangles ke pair banane honge aur jinka base aur parallel lines same ho and find their areas by the method of counting the squares. Each time jab triangles ka area find out karoge to aapko dekhne ko milega ki two triangles ka area (approximately) equal hoga. Aur isko aur ache se samajhne ke liye hum theorems and kuch interesting examples dekhenge.
If a triangle and parallelogram are drawn on the same base and between the same parallel lines, then the area of the triangle is half of the area of the parallelogram.
Example 3
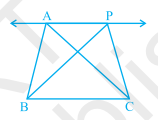
In Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).

GIVEN D is the midpoint of side AB of △ ABC and P is any point on BC. CQ||PD meets AB in Q.
TO PROVE ar(△BPQ)=12ar(△ABC).
CONSTRUCTION Join CD and PQ.
PROOF We know that a median of a triangle divides it into two triangles of equal area.
And, in △ABC, CD is a median.
∴ar(△BCD)=12ar(△ABC)
⇒ar(△BPD)+ar(△DPC)=12ar(△ABC) ...(i)
But, △DPC and DPQ being on the same base DP and between the same parallels DP and CQ, we have
ar(△DPC)=ar(△DPQ) ...(ii)
Using (ii) in(i), we get
ar(△BPQ)+ar(△DPQ)=12ar(△ABC)
∴ar(△BPQ)=12ar(△ABC).
Example 3
In Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).

GIVEN : - D is the midpoint of side AB of △ ABC and P is any point on BC. CQ||PD meets AB in Q.
TO PROVE ar(△BPQ)=12ar(△ABC).
CONSTRUCTION Join CD and PQ.
PROOF We know that a median of a triangle divides it into two triangles of equal area.
And, in △ABC, CD is a median.
∴ar(△BCD)=12ar(△ABC)
⇒ar(△BPD)+ar(△DPC)=12ar(△ABC) ...(i)
But, △DPC and DPQ being on the same base DP and between the same parallels DP and CQ, we have
ar(△DPC)=ar(△DPQ) ...(ii)
Using (ii) in(i), we get
ar(△BPQ)+ar(△DPQ)=12ar(△ABC)
∴ar(△BPQ)=12ar(△ABC).
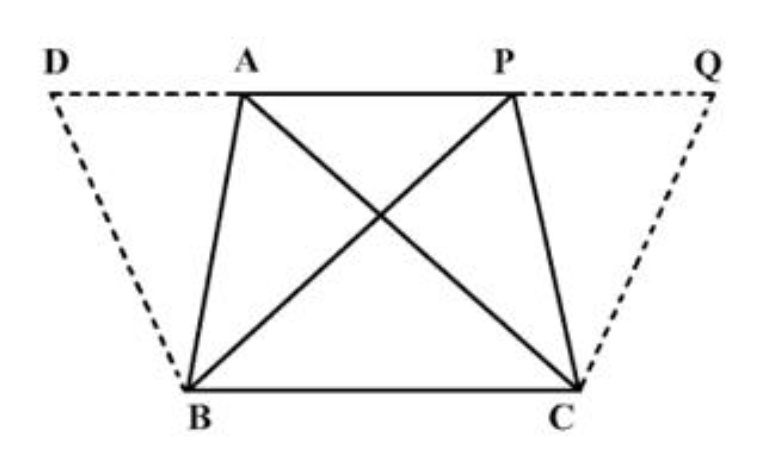
Theorem 9.2
Two triangles on the same base (or equal bases) and between the same parallels are equal in area
Consider the figure given below where △ABE and parallelogram ABCD are drawn on the same base AB and between the same parallels AB and CE.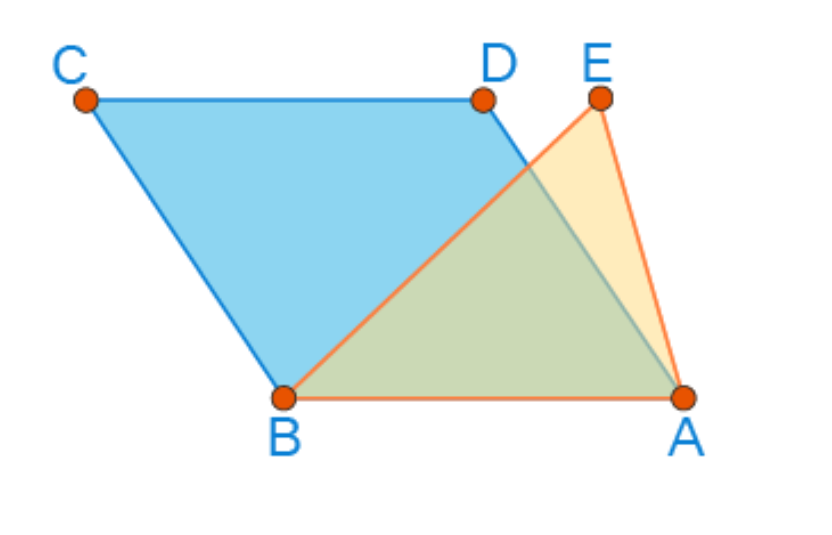
Here, area(△ABE)=12×area (ABCD). Let us prove the above theorem. Complete the parallelogram ABEF as shown below such that the triangle is exactly half of the parallelogram.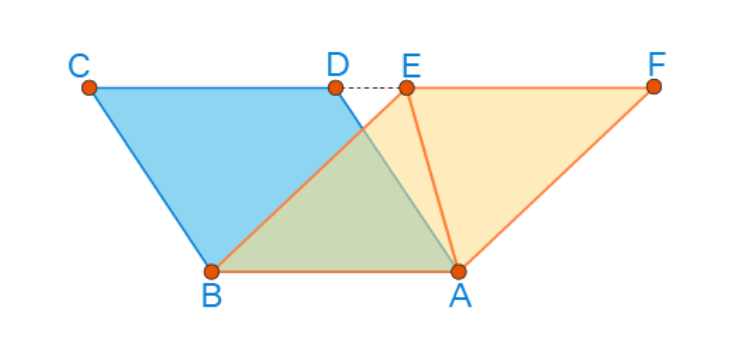
Here, area(△ABE)=12×area (ABEF). But, as we know that two parallelograms on the same base and between the same parallel lines are equal in area. This implies, area (ABCD) = area (ABEF). So, we have,
area(△ABE)=12×area (ABCD)
Hence it is proved that a triangle is half of the area of a parallelogram drawn on the same base and between the same parallels.
Theorem 9.2
Two triangles on the same base (or equal bases) and between the same parallels are equal in area Now, suppose ABCD is a parallelogram whose one of the diagonals is AC
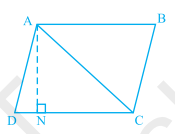
(see Figure 13). Let AN⊥DC. Note that
△ADC≅△CBA (Why?)
So,ar(ADC)=ar(CBA) (Why?)
Therefore, ar(ADC)=1/2ar(ABCD)=1/2(DC×AN) (Why?)
So, area of △ADC = 1/2 ×baseDC× corresponding altitude AN.
Dusre shabdo mei, area of a triangle is half the product of its base (or any side) and the corresponding altitude (or height). Aapko yaad hoga area of triangle ka formula Class VII ? From this formula, two triangles with same base (or equal bases) and equal areas hai toh unke corresponding altitudes equal honge.
Iss result se ek theorem aati hai.
Theorem 9.2
Two triangles on the same base (or equal bases) and between the same parallels are equal in area Now, suppose ABCD is a parallelogram whose one of the diagonals is AC

(see Figure 13). Let AN⊥DC. Note that
△ADC≅△CBA (Why?)
So,ar(ADC)=ar(CBA) (Why?)
Therefore, ar(ADC)=1/2ar(ABCD)=1/2(DC×AN) (Why?)
So, area of △ADC = 1/2 ×baseDC× corresponding altitude AN.
Dusre shabdo mei, area of a triangle is half the product of its base (or any side) and the corresponding altitude (or height). Aapko yaad hoga area of triangle ka formula Class VII ? From this formula, two triangles with same base (or equal bases) and equal areas hai toh unke corresponding altitudes equal honge.
Iss result se ek theorem aati hai.
Example 3
ABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).

Given : A △ABC in which D is the midpoint of BC and E is the important of AD.
To PROVE : ar(△BED)=14ar(△ABC).
Proof : D is the midpoint of BC ⇒ AD is a median of △ ABC
⇒ar(△ABD=ar(△ACD)
[∴ a median divides a △ into two △ of equal area].
⇒ar(△ABD)=12ar(△ABC). ...(i)
E is the midpoint of AD ⇒ BE is a median of △ ABD
⇒ar(△BED)=ar(△BEA)
[∴ a median divides a △ into two △ of equal area].
⇒ar(△BED)=12ar(△ABD)=12{12ar(△ABC)} [using (i)]
⇒ar(△BED)=14ar(△ABC).
Theorem 9.3
: Two triangles having the same base (or equal bases) and equal
areas lie between the same parallels.
Ek example lete hai isko samjhne k liye
Example 4
Show that a median of a triangle divides it into two triangles of equal areas.

Let ABC be a triangle and let AD be one of its medians (see Figure14 ).
You wish to show that ar(ABD)=ar(ACD).
Area k formula mei altitude aata hai, so let us draw AN⊥BC.
Now ar(ABD) = 12 × base × altitude (of ΔABD)
=12×BD×AN
=12×CD×AN (As BD=CD)
= 12 × base × altitude (of △(ACD) = ar(ACD)
Example 4
If the medians of a △ABC intersect at G, show that
ar(△AGB)=ar(△AGC)=ar(△BGC)
=13ar(△ABC).

GIVEN:
A △ABC. Its medians AD,BE and CF intersect at G.
TO PROVE ar(△AGB)=ar(△AGC)=ar(△BGC)=13ar(△ABC)
PROOF:
We know that a median of a triangle divides it into two triangle of equal area.
In △ABC ,AD is the median.
∴ar(△ABD)=ar(△ACD). ...(i)
In △GBC, GD is the median.
∴ar(△GBD)=ar(△GCD). ...(ii)
From (i) and (ii), we get
ar(△ABD)−ar(△GBD)=ar(△ACD)−ar(△GCD)
⇒ar(△AGB)=ar(△AGC).
Similarly, ar(△AGB)=ar(△BGC).
⇒ar(△AGB)=ar(△AGC).
But, ar(△ABC)=ar(△AGB)+ar(△AGC)+ar(△BGC)
=3ar(△AGB) [using (iii)].
∴ar(△AGB)=13ar(△ABC).
Hence, ar(△AGB)=ar(△AGC)=ar(△BGC)=13ar(△ABC).
Example 4
Show that a median of a triangle divides it into two triangles of equal areas.

Let ABC be a triangle and let AD be one of its medians (see Figure14 ).
You wish to show that ar(ABD)=ar(ACD).
Area k formula mei altitude aata hai, so let us draw AN⊥BC.
Now ar(ABD) = 12 × base × altitude (of ΔABD)
=12×BD×AN
=12×CD×AN (As BD=CD)
= 12 × base × altitude (of △(ACD) = ar(ACD)
Example 5
In a triangle ABC, E is the mid-point of median AD. Show that ar (BED)=14ar (ABC)
We know, the median of a triangle, divides the triangle into two triangles of equal areas.
So, in ΔABC
ar(ACD)=ar(ABD)=12ar(ABC)→(1)
Also, we are given,E is the mid-point of AD that means BE is the median of ΔABD
So,
ar(BED)=ar(AEB)=12ar(ABD)
From (1),
ar(BED)=12(12ar(ABC))
ar(BED)=14ar(ABC)
Example 5
In ΔABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).

GIVEN:
D is the midpoint of side AB of △ABC and P is any point on BC. CQ∣∣PD meets AB in Q.
TO PROVE:
ar(△BPQ)=12ar(△ABC).
CONSTRUCTION: Join CD and PQ.
PROOF:
We know that a median of a triangle divides it into two triangles of equal area.
And, in △ABC, CD is a median.
∴ar(△BCD)=12ar(△ABC)
⇒ar(△BPD)+ar(△DPC)=12ar(△ABC) ...(i)
But, △DPC and DPQ being on the same base DP and between the same parallels DP and CQ, we have
ar(△DPC)=ar(△DPQ) ...(ii)
Using (ii) in(i), we get
ar(△BPQ)+ar(△DPQ)=12ar(△ABC)
∴ar(△BPQ)=12ar(△ABC).
Example 5
In a triangle ABC, E is the mid-point of median AD. Show that ar (BED)=14ar (ABC)
We know, the median of a triangle, divides the triangle into two triangles of equal areas.
So, in ΔABC
ar(ACD)=ar(ABD)=12ar(ABC)→(1)
Also, we are given,E is the mid-point of AD that means BE is the median of ΔABD
So,
ar(BED)=ar(AEB)=12ar(ABD)
From (1),
ar(BED)=12(12ar(ABC))
ar(BED)=14ar(ABC)
Example 6
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show thatar (APB) × ar (CPD) = ar (APD) × ar (BPC).
Let us draw a point X and N on BD such that
AN⊥BD and CX⊥BD.
Then,
L.H.S.=ar(APB)×ar(CPD)
12(AN)(PB)×12(CX)(PD)
12(AN)(PD)×12(CX)(PB)
ar(APD)×ar(BPC)=R.H.S.
ANGLES ON SAME BASE AND WITH EQUAL AREAS
Baccho, humari next theorem is based on the previous one. According to this theorem, if two triangles of equal area lie on the same base, then they lie between same parallels as well.
Example 6
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show thatar (APB) × ar (CPD) = ar (APD) × ar (BPC).
Let us draw a point X and N on BD such that
AN⊥BD and CX⊥BD.
Then,
L.H.S.=ar(APB)×ar(CPD)
12(AN)(PB)×12(CX)(PD)
12(AN)(PD)×12(CX)(PB)
ar(APD)×ar(BPC)=R.H.S.
Example 7
Show that a median of a triangle divides it into two triangles of equal areas.
Please refer to the diagram in the video.
Here, AD is median to BC such that BD=CD
and AE⊥BC.
ar(ABD)=12×AE×BD
=12×AE×CD(as BD=CD)
=ar(ACD)
As, ar(ABD)=ar(ACD),
it shows a median of a triangle divides it into two triangles of equal areas.
Theorem 9.3
Two triangles having the same base (or equal bases) and equal areas lie between the same parallels
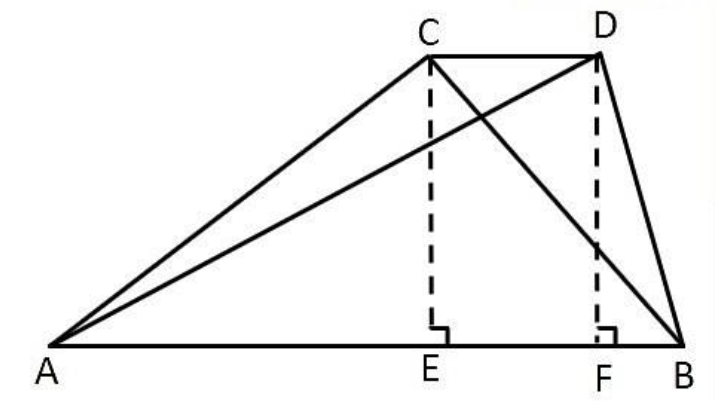
Given: △ABC and △ABD are two triangles on same base AB such that area(△ABC)=area(△ABD).
Join CD
To prove: CD∣∣AB
Construction: Draw the altitudes of △ABC and △ABD through C and D and meeting base at E and F respectively.
Proof: Since CE⊥AB and DF⊥AB (by construction)
Since, lines perpendicular to same line are parallel to each other.
∴CE∣∣DF .......(1)
Now, area(△ABC)=12×AB×CE
area(△ABD)=12×AB×DF
Since , area(△ABC)=area(△ABD)(Given)
∴CF=DF .........(2)
Now, In CDFE,CF∣∣DF and CE∣∣DF
Since one pair of opposite sides are equal and parallel.
Hence CDFE is a parallelogram.
So, CD∣∣EF (opposite sides of parallelogram are parallel)
∴CD∣∣AB
Hence, proved.
Example 7
Show that a median of a triangle divides it into two triangles of equal areas.
Please refer to the diagram in the video.
Here, AD is median to BC such that BD=CD
and AE⊥BC.
ar(ABD)=12×AE×BD
=12×AE×CD(as BD=CD)
=ar(ACD)
As, ar(ABD)=ar(ACD),
it shows a median of a triangle divides it into two triangles of equal areas.
Summary
In this chapter, you have studied the following points:
- Area of a figure is a number (in some unit) associated with the part of the plane enclosed by that figure.
- Two congruent figures have equal areas but the converse need not be true.
- If a planar region formed by a figure T is made up of two non-overlapping planar regions formed by figures P and Q, then ar (T) = ar (P) + ar (Q), where ar (X) denotes the area of figure X.
- Two figures are said to be on the same base and between the same parallels, if they have a common base (side) and the vertices, (or the vertex) opposite to the common base of each figure lie on a line parallel to the base.
- Parallelograms on the same base (or equal bases) and between the same parallels are equal in area.
- Area of a parallelogram is the product of its base and the corresponding altitude.
- Parallelograms on the same base (or equal bases) and having equal areas lie between the same parallels.
- If a parallelogram and a triangle are on the same base and between the same parallels, then area of the triangle is half the area of the parallelogram.
- Triangles on the same base (or equal bases) and between the same parallels are equal in area.
- Area of a triangle is half the product of its base and the corresponding altitude.
- Triangles on the same base (or equal bases) and having equal areas lie between the same parallels.
- A median of a triangle divides it into two triangles of equal areas.
Example 6
Show that a median of a triangle divides it into two triangles of equal areas.
Please refer to the diagram in the video.
Here, AD is median to BC such that BD=CD
and AE⊥BC.
ar(ABD)=12×AE×BD
=12×AE×CD(as BD=CD)
=ar(ACD)
As, ar(ABD)=ar(ACD),
it shows a median of a triangle divides it into two triangles of equal areas.
Summary
In this chapter, you have studied the following points:
- Area of a figure is a number (in some unit) associated with the part of the plane enclosed by that figure.
- Two congruent figures have equal areas but the converse need not be true.
- If a planar region formed by a figure T is made up of two non-overlapping planar regions formed by figures P and Q, then ar (T) = ar (P) + ar (Q), where ar (X) denotes the area of figure X.
- Two figures are said to be on the same base and between the same parallels, if they have a common base (side) and the vertices, (or the vertex) opposite to the common base of each figure lie on a line parallel to the base.
- Parallelograms on the same base (or equal bases) and between the same parallels are equal in area.
- Area of a parallelogram is the product of its base and the corresponding altitude.
- Parallelograms on the same base (or equal bases) and having equal areas lie between the same parallels.
- If a parallelogram and a triangle are on the same base and between the same parallels, then area of the triangle is half the area of the parallelogram.
- Triangles on the same base (or equal bases) and between the same parallels are equal in area.
- Area of a triangle is half the product of its base and the corresponding altitude.
- Triangles on the same base (or equal bases) and having equal areas lie between the same parallels.
- A median of a triangle divides it into two triangles of equal areas.
Example 7
In a triangle ABC, E is the mid-point of median AD. Show that ar (BED)=14ar (ABC)
We know, the median of a triangle, divides the triangle into two triangles of equal areas.
So, in ΔABC
ar(ACD)=ar(ABD)=12ar(ABC)→(1)
Also, we are given,E is the mid-point of AD that means BE is the median of ΔABD
So,
ar(BED)=ar(AEB)=12ar(ABD)
From (1),
ar(BED)=12(12ar(ABC))
ar(BED)=14ar(ABC)
Example 8
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show thatar (APB) × ar (CPD) = ar (APD) × ar (BPC).
Let us draw a point X and N on BD such that
AN⊥BD and CX⊥BD.
Then,
L.H.S.=ar(APB)×ar(CPD)
12(AN)(PB)×12(CX)(PD)
12(AN)(PD)×12(CX)(PB)
ar(APD)×ar(BPC)=R.H.S.
Example 9
Show that a median of a triangle divides it into two triangles of equal areas.
Please refer to the diagram in the video.
Here, AD is median to BC such that BD=CD
and AE⊥BC.
ar(ABD)=12×AE×BD
=12×AE×CD(as BD=CD)
=ar(ACD)
As, ar(ABD)=ar(ACD),
it shows a median of a triangle divides it into two triangles of equal areas.
Summarize
In this chapter, you have studied the following points:
- Area of a figure is a number (in some unit) associated with the part of the plane enclosed by that figure.
- Two congruent figures have equal areas but the converse need not be true.
- If a planar region formed by a figure T is made up of two non-overlapping planar regions formed by figures P and Q, then ar (T) = ar (P) + ar (Q), where ar (X) denotes the area of figure X.
- Two figures are said to be on the same base and between the same parallels, if they have a common base (side) and the vertices, (or the vertex) opposite to the common base of each figure lie on a line parallel to the base.
- Parallelograms on the same base (or equal bases) and between the same parallels are equal in area.
- Area of a parallelogram is the product of its base and the corresponding altitude.
- Parallelograms on the same base (or equal bases) and having equal areas lie between the same parallels.
- If a parallelogram and a triangle are on the same base and between the same parallels, then area of the triangle is half the area of the parallelogram.
- Triangles on the same base (or equal bases) and between the same parallels are equal in area.
- Area of a triangle is half the product of its base and the corresponding altitude.
- Triangles on the same base (or equal bases) and having equal areas lie between the same parallels.
- A median of a triangle divides it into two triangles of equal areas.
Let's Revise
1. Baccho iss chapter m humne parallelograms aur triangles k areas se related theorems k baare m pdha jisse hume unke alag alag relations k baare m pta chla.
2. Area ek enclosed region ko kaha jaata hai. Saare 2D geometrical shapes k areas hote hai. Jab do figures k shape, size aur areas equal hote hai to vo congruent figures kehlaati hai.
3. Jab do parallelograms same base aur same parallels k beech , hote hai to unke areas bhi equal hote hai. Iss theorem ka converse bhi true hai.
4. Jab do triangles same base p aur same parallels k beech m hote hai to unke areas equal hojate hai. Iss theorem ka converse also hold true.
5. Jab ek parallelogram aur ek triangle same base aur same parallels k beech m lie krte hai to triangle ka area becomes half of the area of the parallelogram.
6. The area of a triangle is half the product of its base and the corresponding altitude.
7. Triangle ka median use do equal parts m divide krta hai.
