गणितीय आगमन का सिद्धांत कक्षा 11 गणित
भूमिका
गणितीय आगमन एक तकनीक (technique) है जिसका प्रयोग विविध प्रकार के गणितीय कथनों का सूत्रिकरण करने में किया जा सकता है, जो n के पदों में सूत्रबद्ध हों, जहाँ n एक धन पूर्णांक है। इस अध्याय मे हम देखेंगे आगमन सिद्धांत की प्रेरणा कहाँ से आयी तथा इस सिद्धांत को समझने का प्रयास करेंगे।
आइए बच्चों इस अध्याय को करीब से समझते है...
गणितीय आगमन गणितीय उपपत्ति प्रस्तुत करने की एक विधि है जिसका उपयोग प्रायः यह दर्शाने के लिये किया जाता है कि कोई कथन सभी प्राकृतिक संख्याओं के लिये सत्य है। इस प्रकार हम कह सकते है बीजगणित में या गणित की अन्य शाखाओं में कुछ ऐसे परिणाम या कथन होते हैं जिन्हें एक धन पूर्णांक n के पदों में व्यक्त किया जाता है। ऐसे कथनों को सिद्ध करने के लिए विशिष्ट तकनीक पर आधारित समुचित सिद्धांत है जो गणितीय आगमन का सिद्धांत (Principle of Mathematical Induction) कहलाता है।
गणितीय आगमन के सिद्धांत के अनुसार प्राकृत सँख्या n से संबंधित कोई साध्य सभी n≥k के लिए सही होगा यदि
- P(k) सत्य हो अर्थात साध्य (conditional Proposition) P(n), n=k के लिए सत्य हो।
- P(m+1) सत्य हो जब कभी P(m) सत्य हो अर्थात साध्य P(n), n = m के लिए सत्य होने पर n=m+1 के लिए भी सत्य है, जहाँ m≥k
अब यहाँ हम साध्य (Proposition) को समझने का प्रयास करते है...
- वह कथन जो या तो सत्य हो या असत्य हो साध्य कहलाता है, अब आपको ऐसा लग रहा होगा की प्रत्येक कथन अवश्य ही सत्य या असत्य होगा परन्तु ऐसा नहीं है। जैसे की कथन "कक्षा 12 मे पढ़ने वाला प्रत्येक छात्र IIT की परीक्षा मे सफल होता है" यह कथन साध्य नहीं है क्योंकि यह हम नहीं कह सकते है प्रत्येक छात्र IIT परीक्षा मे सफल होगा अथवा नहीं अर्थात हम नहीं बता सकते की कथन सत्य है या असत्य।
प्राकृत सँख्या n से संबंधित किसी सूत्र को स्थापित करने या किसी साध्य को साबित करने मे गणितीय आगमन सिद्धांत का प्रयोग किया जाता है। प्राकृत सँख्या n मे किसी साध्य को संकेत के रूप मे साधारणतः P(n) से दर्शाया जाता है, जैसा की हमने ऊपर दर्शाया है।
व्यावहारिक जीवन में आगमन के सिद्धांत को एक उदाहरण के माध्यम से समझने का प्रयास करते है :
मान लेते है किसी किसी तल पर कुछ टाइल्स एक समांतर क्रम में व्यवस्थित किये गए है जैसा की नीचे चित्र में दिखाया गया है
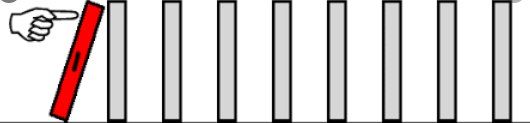
अब यदि हम पहली टाइल को धक्के से गिराते है तो हम देखते है कि पहली टाइल अपने बाद वाली (अनुवर्ती) टाइल को गिरा देती है और यह घटना अन्य आगे रखी टॉइल्स में बढ़ती जाती है।
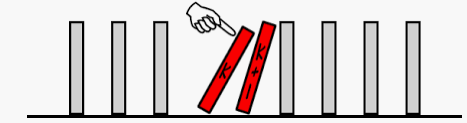
इसी प्रकार कोई k वीं टाइल रखी हुई है जो क्रम मे है उसे धक्का देने से k+1 वीं, k+2 वीं टाइल क्रमशः गिरेगी, तो हम इस घटना से यह अनुमान लगा सकते है की इस क्रम में जितनी भी टाइल्स रखी होगी वे सभी इस घटना के अनुरूप गिरती जाएगी।
यही विश्लेषण ही गणितीय आगमन के सिद्धांत का आधार है।
हम जानते हैं कि प्राकृत संख्याओं का समुच्चय N वास्तविक संख्याओं का विशेष क्रमित उपसमुच्चय है। वास्तव में, R का सबसे छोटा उपसमुच्चय N है, जिसमें निम्नलिखित गुण हैं:
एक समुच्चय S आगमनिक समुच्चय (Inductive set) कहलाता है यदि 1∈S और x+1∈S जब कभी x∈S क्योंकि N, जो कि एक आगमनिक समुच्चय है, R का सबसे छोटा उपसमुच्चय है, परिणामतः R के किसी भी ऐसे उपसमुच्चय में जो आगमनिक है, N अनिवार्य रूप से समाहित होता है।
प्राकृतिक संख्याओं के समुच्चय N में यदि A⊂N तब :
(i)1∈A
(ii) यदि a∈A⇔a+1∈A तो A=N
आगमनिक समुच्चय
प्राकृतिक संख्याओं के समुच्चय N का एक ऐसा उपसमुच्चय Sn जो प्रथम n क्रमागत प्राकृतिक संख्याओं को लेने से प्राप्त होता है, आगमनिक समुच्चय (Inductive set) कहलाता है।
यदि k∈Sn और k≤n
तब k+1∈Sn
गणितीय आगमन का सिद्धांत
माना धन पूर्णांकों से सम्बंधित एक कथन P(n) दिया गया है। तो इस कथन की सत्यता की जांच निम्न चरणों द्वारा की जाती है
दिया गया कथन n=k+1 के लिए सत्य है तो हम यह निर्णय ले सकते है कि कथन P(n) सभी प्राकृत संख्या n के लिए सत्य है।
आइए इसके लिए एक महत्वपूर्ण परिणाम देखते है :
प्राकृतिक संख्याओ के `n` पदों का योग
P(n)=1+2+3+4+...............+n=n(n+1)2,
n के सभी प्राकृतिक मानों के लिये सत्य है।
step 1-
सर्वप्रथम यह दिखाएं कि यह कथन n=1 के लिये सत्य है।
P(1) का मतलब निम्नलिखित कथन होगा-
1(1+1)2=1
स्पष्टतः यह कथन सत्य है क्योंकि इसका दायां पक्ष और बांयां पक्ष दोनो ही एक हैं (अतः समान हैं)
अतः n=1 के लिये कथन सत्य है (अर्थात् P(1) सत्य है।)
step 2-
अब हम यह मानेंगे कि प्रथम k प्राकृतिक संख्याओं के लिए भी अर्थात n=k के लिए भी दिया गया कथन सत्य है अर्थात
1+2+3+4+5+...............+k
=k(k+1)2.....(i)
तो हमें सिद्ध करना हैं कि P(k+1) भी सत्य है। अर्थात
हमें सिद्ध करना हैं
1+2+3+4+5+......................+k+(k+1)
=(k+1)(k+2)2
उपपति -
समीकरण 1 में दोनों तरफ k+1 जोड़ने पर
1+2+3+4+5+......................+k+(k+1)
=(k)(k+1)2+(k+1)
⇒(k+1)[k2+1]
=(k+1)(k+2)2
इससे प्रदर्शित हुआ कि वास्तव में P(k+1) भी सत्य है।
इस प्रकार गणितीय आगमन से सिद्ध हुआ कि उपरोक्त कथन P(n),n के सभी प्राकृतिक मानों के लिये सत्य है।
इतिसिद्धम
गुण - यदि कोई दिया गया कथन P(n) ,n≥4 के सभी मानों के लिए कथन सत्य हो तो इस स्थिति में प्रथम चरण n=4 से प्रारंभ होगा और हम सर्वप्रथम परिणाम को n=4 के लिए अर्थात् P(4) के लिए सत्यापित करेंगे ।
OMR (One Minute Revision)
चरण 1 सर्वप्रथम कथन P(n) की n=1 लिए सत्यता की जांच करे।
चरण 2 - यदि कथन P(n), n=1 के लिए सत्य है तो कल्पना करे कि यह n=k के लिए P(k) सत्य है।
चरण 3 - सिद्ध करे की कथन n=k+1 के लिए भी सत्य है। यदि यह सत्य साबित हुआ तो हम कह सकते है क़ि कथन P(n) सभी प्राकृतिक संख्याओं के लिए सत्य है।
उदाहरण 1
सभी n≥1 के लिए, सिद्ध कीजिए
12+22+32+42+...+n2=n(n+1)(2n+1)6
मान लीजिए कि दिया कथन P(n) है,अर्थात्
P(n):12+22+32+42+...+n2=n(n+1)(2n+1)6
n=1 के लिए
चूंकि कथन में योग वाला अनुक्रम दिया गया है इसलिए n=1 के लिए बाएं पक्ष से केवल पहला पद (12) लेंगे और दायें पक्ष में n=1 मान रखेंगे
P(1):=1(1+1)(2×1+1)6
P(1):=1×2×36=1
जो कि सत्य है
किसी धन पूर्णांक k के लिए कल्पना कीज़ए कि P(k) सत्य है, अर्थात्
12+22+32+42+...+k2=k(k+1)(2k+1)6 ....(i)
अब हम सिद्ध करेंगे कि P(k+1) भी सत्य है,
(12+22+32+42+...+k2)+(k+1)2
=k(k+1)(2k+1)6+(k+1)2 [(i) के प्रयोग से]
=k(k+1)(2k+1)+6(k+1)26
=(k+1)(2k2+7k+6)6
=(k+1)(2k2+4k+3k+6)6
=(k+1)(2k(k+2)+3(k+2))6
=(k+1)((k+2)(2k+3))6
=(k+1)((k+1+1)(2k+2+1))6
=(k+1)(k+1+1){2(k+1)+1}6
=(k+1)((k+1)+1){2(k+1)+1}6
इस प्रकार P(k+1) सत्य है जब कभी P(k) सत्य है।
अतः गणितीय आगमन सिद्धांत से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है।
उदाहरण 2
गणितीय आगमन सिद्धांत से साबित कीजिए कि
11.2+12.3+.....+1n(n+1)=nn+1
माना कि
P(n):11.2+12.3+….+1n(n+1)=nn+1
Step I. जब n=1,L.H.S=11.2=12
तथा R.H.S=nn+1=11+1=12
∴L.H.S.=R.H.S
अतः P(1) सत्य है।
माना कि P(m) सत्य है तो
11.2+12.3+………+1m(m+1)=mm+1....(i)
साबित करना है कि P(m+1) सत्य है।
अतः P(m+1): 11.2+12.3+….+1m(m+1)+1(m+1)(m+1+1)
अंतिम पद को छोड़कर शुरू के सभी पदों के योग का मान समी (i) से रखने पर
=mm+1+1(m+1)(m+2)
=m(m+2)+1(m+1)(m+2)
=m2+2m+1(m+1)(m+2)
=(m+1)2(m+1)(m+2)
=m+1m+2
=m+1(m+1)+1....(ii)
समीकरण (ii) से हमने सिद्ध किया कि P(m) सत्य होने पर P(m+1) भी सत्य है।
अतः कथन P(n) गणितीय आगमन के सिद्धांत से सभी प्राकृत संख्या n के लिए सत्य है।
उदाहरण 3
x>−1 के लिए सभी प्राकृत संख्याओं n के लिए साबित कीजिए कि
(1+x)n≥(1+nx)
माना कि,
P(n):(1+x)n≥(1+nx) जहाँ x>−1
जब n=1
L.H.S=(1+x) तथा R.H.S=(1+x)
∴ जब n=1, (1+x)n=1+nx
अतः (1+x)n≥1+nx सत्य है जब n=1
∴P(1) सत्य है।
माना कि P(m) सत्य है
⇒(1+x)m≥(1+mx).....(i)
साबित करना है कि P(m+1) सत्य है।
अर्थात P(m+1): ⇒(1+x)1+m≥(1+(1+m)x)=α (माना).....(ii)
(सिद्ध करना है)
अब समीकरण (i) के दोनों तरफ (1+x) से गुणा करने पर
(1+x)m⋅(1+x)≥(1+mx)(1+x)
(1+x)m+1≥(1+mx)(1+x)=β (माना).....(iii)
ध्यान दीजिए यहाँ हमने समी (ii) एवं (iii) के दायें पक्ष को क्रमशः α एवं β माना है
अबβ−α=(1+mx)(1+x)−1−(m+1)x
β−α =1+mx+x+mx2−1−mx−x
=mx2>0
चूंकि m एक प्राकृत संख्या है और किसी भी वास्तविक संख्या का वर्ग (x2) हमेशा धनात्मक होता है
∴mx2>0
β−α>0
∴β>α…………(iv)
समीकरण (iii) तथा (iv) से
(1+x)m+1>α
⇒(1+x)m+1>1+(m+1)x. [(ii) से]
अतः P(m) सत्य होने पर P(m+1) सत्य होगा। ……..B
समीकरण A तथा B से, गणितीय आगमन सिद्धांत से सभी प्राकृत संख्याओं n के लिए P(n) सत्य है।
उदाहरण 4
प्रत्येक धन पूर्णांक n के लिए सिद्ध कीजिए कि 7n−3n,4 से विभाजित होता है।
मान लीजिए दिया कथन P(n):7n−3n,4 से विभाजित है।
हम पाते हैं P(1):71−31=4 जो कि 4 से विभाजित होता है। इस प्रकार P(n),n=1 के लिए सत्य है।
कल्पना कीजिए कि एक धन पूर्णांक k के लिए P(k) सत्य है।
अर्थात, P(k):7k−3k,4 से विभाजित होता है।
अतः हम लिख सकते हैं 7k−3k=4d जहाँ d∈N
अब हम सिद्ध करना चाहते हैं कि P(k+1) सत्य है, जब कभी P(k) सत्य है।
अब 7(k+1)−3(k+1)
=7(k+1)−7.3k+7.3k−3(k+1)
=7(7k−3k)+(7−3)3k
=7(4d)+(7−3)3k
=7(4d)+4.3k
=4(7d+3k)
यहाँ देख सकते है की 4⋅(7d+3k), 4 से पूर्णतः विभाजित है।
अतः P(k) सत्य होने पर, P(k+1) सत्य है।
इस प्रकार गणितीय आगमन से सिद्ध हुआ कि उपरोक्त कथन P(n),n के सभी प्राकृतिक मानों के लिये सत्य है।
उदाहरण 5
यदि n≥2 तो आगमन सिद्धांत से साबित करें कि n4<10n
माना कि,
P(n):n4<10n,n≥2
जब n=2, L.H.S =24=16 तथा R.H.S=102=100
∴16<100∴P(2) सत्य है …….(A)
माना कि P(m) सत्य है तो m4<10m
अर्थात 10m>m4………..(1)
साबित करना है कि P(m+1) सत्य है अर्थात (m+1)4<10m+1 अर्थात
10m+1>(m+1)4
=α (माना) …...(2)
अर्थात 10m+1≥α,
जहां α=(m+1)4
समीकरण (1) के दोनों तरफ 10 से गुणा करने पर
10m⋅10>10m4
10m+1>10m4=β माना
अर्थात 10m+1>β
जहां β=10m4……(3)
अब βα=10m4(m+1)4
βα=10(mm+1)4
चूँकि
m≥2
दोनों पक्षों में 1 जोड़ने पर
∴m+1≥3
व्युत्क्रम करने पर असमिका के चिह्न बदल जाते हैं
⇒13≥1m+1
−1 का गुणा करने पर असमिका के चिह्न बदल जाते हैं
⇒−1m+1≥−13
दोनों पक्षों में 1 जोड़ने पर-
⇒1−1m+1≥1−13
⇒mm+1≥23
⇒(mm+1)4≥(23)4
⇒10(mm+1)4≥10.1681≥1
∴ समी (3) से βα≥1=β>α ….(4)
समीकरण 2 और 4 से
10m+1>α
अर्थात 10m+1>(m+1)4
∴P(m) सत्य होने पर P(m+1) सत्य होगा ….(B)
समीकरण A और B से, आगमन सिद्धांत से सभी प्राकृत संख्याओं n≥2 के लिए P(n) सत्य है।
सारांश
गणितीय आगमन (Mathematical induction) गणितीय उपपत्ति (Mathematical Proof) प्रस्तुत करने की एक विधि है जिसका उपयोग प्रायः यह दर्शाने के लिये किया जाता है कि कोई कथन (statement) सभी प्राकृतिक संख्याओं के लिये सत्य है।
चरण 1 सर्वप्रथम कथन P(n) की n=1 लिए सत्यता की जांच करे।
चरण 2 - यदि कथन P(n), n=1 के लिए सत्य है तो कल्पना करे कि यह n=k के लिए P(k) सत्य है।
चरण 3 - सिद्ध करे की कथन n=k+1 के लिए भी सत्य है। यदि यह सत्य साबित हुआ तो हम कह सकते है क़ि कथन P(n) सभी प्राकृतिक संख्याओं के लिए सत्य है।
कुछ स्मरण रखने योग्य श्रेणियों के n पदों का योग-
=n(n+1)2
=n2
=n(n+1)(2n+1)6
=[n(n+1)2]2
=a(1−rn)1−r
