Complete Solutions to PROBLEMS FOR PRACTIVE of chapter GRAVIATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVIATION |
| PRADEEP | PROBLEMS FOR PRACTIVE |
| Number Of Questions | 47 |
| Academic Year | 2023-24 |
Two satelites of a planet have period 32 days and 256 days. If the radius of orbit of former is R, find the orbital radius of the latter.
03:16View SolutionA geostationary satellite is orbiting the Earth at a height of `6 R` above the surface of Earth, where `R` is the radius of the Earth. The time period of another satellites is `6 sqrt(2) h`. Find its height from the surface of Earth.
03:11View SolutionA geo-stationary stellite orbits around the earth in a circular orbit of radius 36,000km. Then, the time period of a spy stellite orbitting a few hundred km above the earth's surface `(R_(earth) = 6400km)` will approximately be
02:33View SolutionIf the distance between the earth and the sun were half its present value, the number of days in a year would have been
02:20View SolutionHow fast (in `m^(2) s^(-1))` is area swept out by (a) the radius from sun to earth ? (b) the radius from the sun to earth `= 1.496 xx 10^(11) m` , Distance of earth to moon `= 3.845 xx 10^(8) m` and period of revolution of moon `= 27 (1)/(3)` days.
02:55View SolutionEstimate the mass of the sun, assuning the orbit of Earth round the sun to be a circule. The disatnce between the sun and the Earth is `1.49 xx 10^(11) m`, and `G = 6.67 xx 10^(-11) Nm^(2) kg^(-2)`.
03:33View SolutionA spherical mass of `20 kg` lying on the surface of the Earth is attracted by another spherical mass of `150 kg` with a force equal to `0.23 mg f`. The centres of the two masses are `30 cm` apart. Calculate the mass of the Earth. Radius of the Earth is `6 xx 10^(6)m`.
03:19View SolutionThere is a point between the earth and the moon, where the gravitational force on a space ship due to earth and moon together is zero. Find the distance of that point from the earth Given the disatnce between earth and moon is `3.845 x 10^(8) m` and the moon has `1.2 %` of the mass of the earth.
04:05View SolutionThree point mass bodies of masses `m, 2m` and `4m` are placed at `A, B` and `C` as shown in fig. where `AB = BC = l`.
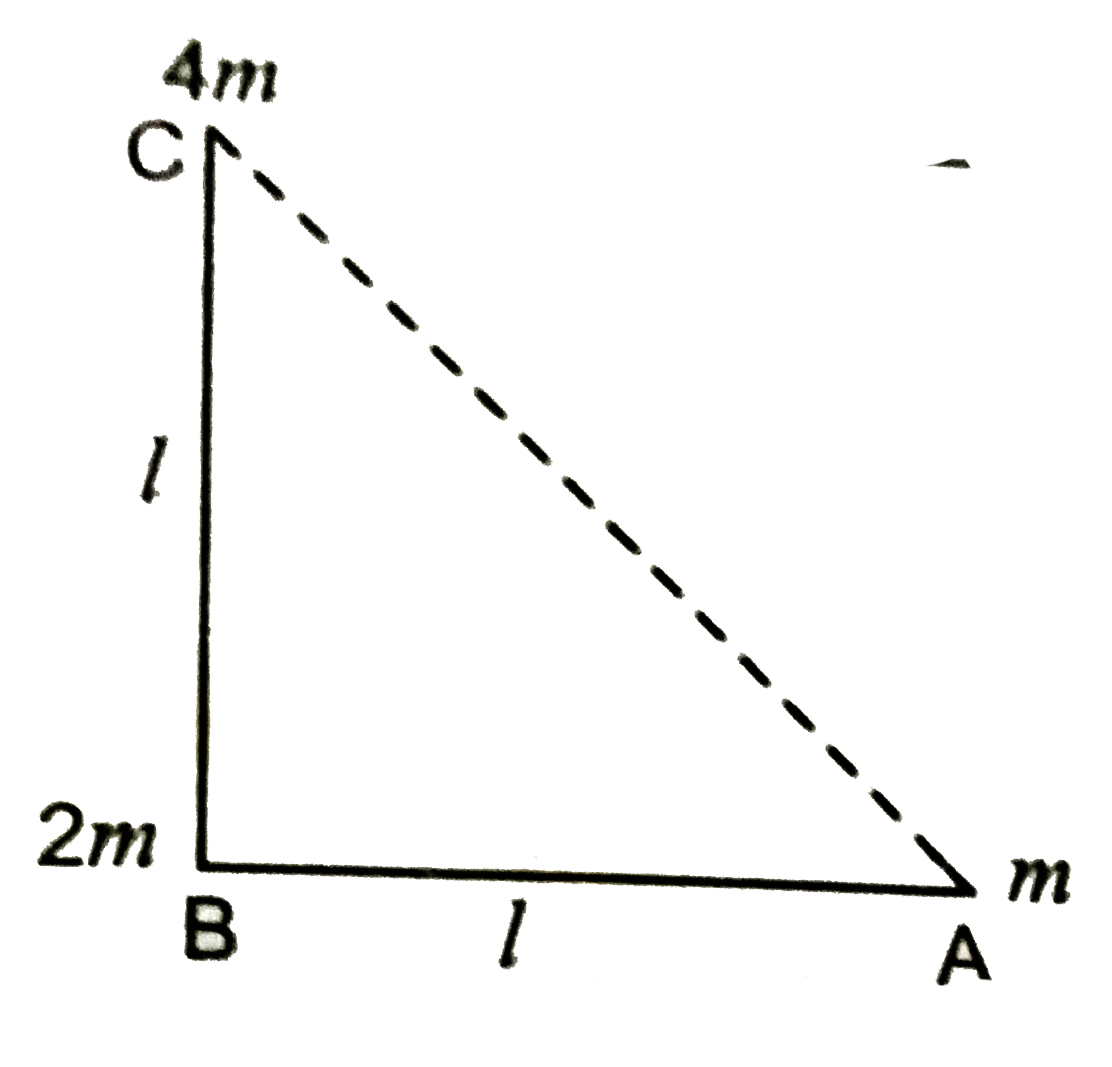
Find the magnitude of the resulatant gravitational pull on body at `A` due to bodies at `B` and `C`.04:24View SolutionFour point mass bodies of masses as shown in Fig. are placed at the vertices of a square `ABCD`, gravitational force on the body at `A`. Given, `G = 6.6 xx 10^(-11) Nm^(2) kg^(-2)`
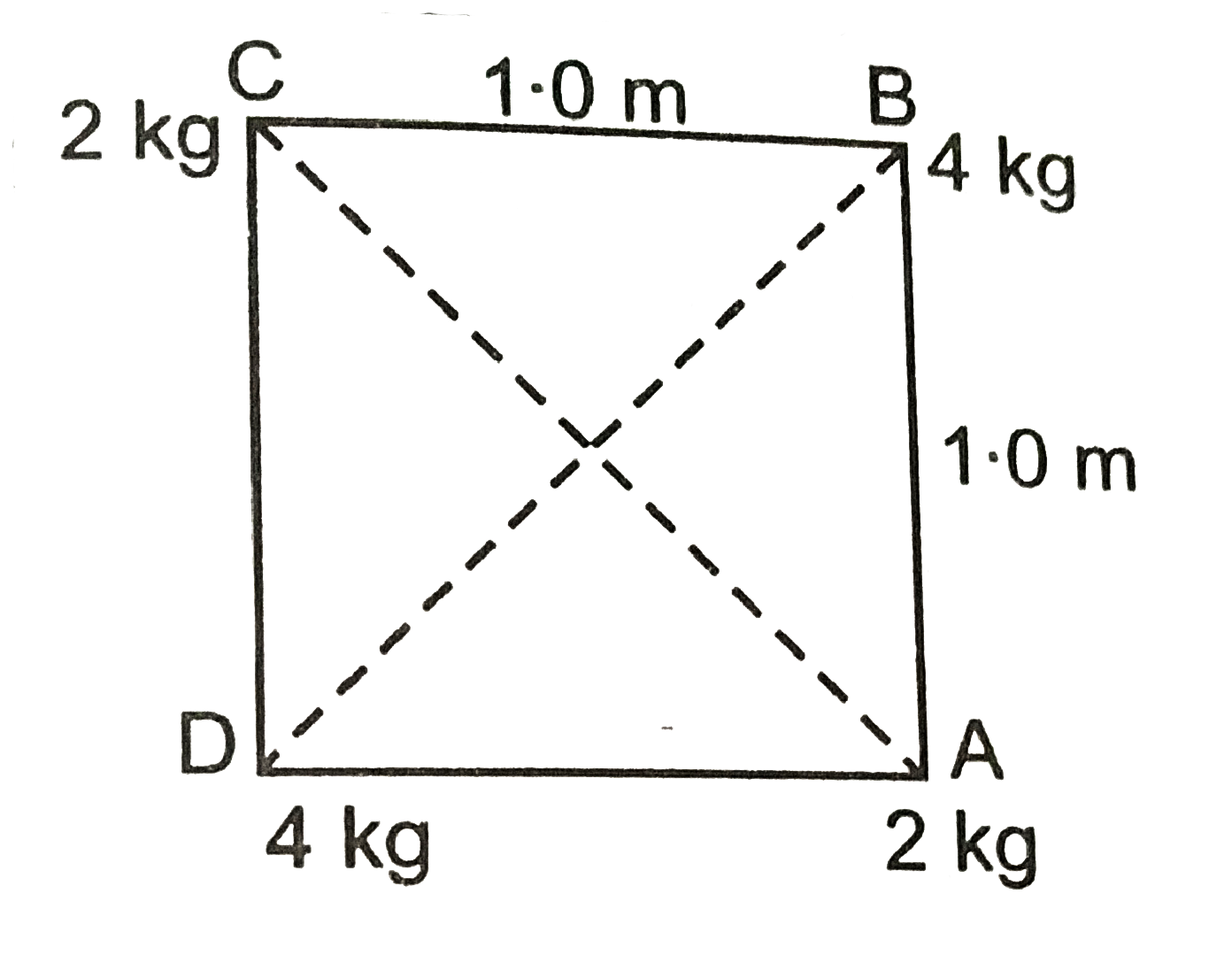 04:40View Solution
04:40View SolutionIf the radius of the Earth shrinks by `2%`, mass remaing same, then how would the have of acceleration due to gravity change?
04:47View SolutionA body weighs `54 kg f` on the surface of Earth. How much will it weigh on the surface of mers whose mass is `1//9` and the redius is `1//2` of that of earth?
03:19View SolutionThe weight of a person on the Earth is `80 kg`. What will be his weight on the Moon ? Mass of the Moon `= 7.34 xx 10^(22) kg`, radius `= 1.75 xx 10^(6) m` and gravitational constant `= 6.67 xx 10^(-11) N m^(2) kg^(-2)`. What will be the mass of the person at the Moon and acceleration due to gravity there ? If this person can jump `2 m` high on the Earth, how much high can he jump at the Moon ?
05:11View SolutionIf the Earth were made of lead of relative density `11.4`, then find the value of acceleration due to gravity on the surface of Earth ? Radius of the Earth is `6400 km` and `G = 6.67 xx 10^(-11) Nm^(2) kg^(-2)`.
02:50View SolutionA spherical mass of `20 kg` lying on the surface of the Earth is attracted by another spherical mass of `150 kg` with a force equal to `0.23 mg f`. The centres o fthe two masses are `30 cm` apart. Calculate the mass of the Earth. Radius of the Earth is `6 xx 10^(6)m`.
03:19View SolutionThe radius of earth is about `6400Km` and that of mars is about `3200 km` The mass of the earth is about `10`times the mass of mars. An object weight `200N` on earth 's surface, then its weight on the surface of mars will be:
03:57View SolutionThe value of acceleration due to gravity at the surface of the earth is `9.8 ms^(-2)` and the mean radius is about `6.4 xx 10^(6) m`. Assuming that we could get more soil some where, estimate how thick would an added uniform outer layer on the earth have to have the value of acceleration due to gravity `10 ms^(-2)` exactly ?
03:47View SolutionHow much above the surface of earth does the accelration due to gravity reduces by `64%` of its value on the earth. Radius of earth `= 6400 km`.
02:14View SolutionHow much above the surface of earth does the accelration due to gravity reduces by `64%` of its value on the earth. Radius of earth `= 6400 km`.
02:14View SolutionA particle hanging from a spring stretches it by 1 cm at earth's surface. How much will the same particle stretch the spring at a place 800 km above the earth's surface/ Radius of the earth=6400 km.
03:26View SolutionAssuming the Earth to be a sphere of uniform mass density, how much would a body weight half way down to the centre of the Earth, if it weighed `300N` on the surface of Earth.
02:00View SolutionCompare the weights of a body when it is
(i) `200 km` above the surface of the Earth and
(ii) `200 km` below the surface of Earth. Radius of the Earth is `6400 km`.04:15View SolutionThe acceleration due to gravity at a height `1km` above the earth is the same as at a depth `d` below the surface of earth. Then :
03:04View SolutionFind the percentage decrease in the weight of the body when taken to a depth of `32 km` below the surface of earth. Radius of the earth is `6400 km`.
02:31View SolutionA body of mass `10 kg` is taken from equator to pole of the Earth. Calculate the change in its weight, if the radius of the Earth is `6.38 xx 10^(6) m`, time period of Earth's rotation about its polar axis is `24` hours.
03:13View SolutionAt what rate should the earth rotate so that the apparent g at the equator becomes zero? What will be the length of the day in this situation?
02:12View SolutionCalculate the value of acceleration due to gravity at a place of lititude `30^(@)`. Radius of the Earth `6.4xx 10^(6)m`.The value of acceleration due to gravity on Earth is `9.8 m//s^(2)`.
02:22View SolutionHow far from Earth must a body be along a line joining the sun to the earth so that resultage gravitational pull on the body due to Earth and sun is zero ? Distance between sun and the Earth is `1.5 xx 10^(8) km`. Mass of sun `= 3.25 xx 10^(5)` times mass of Earth.
03:59View Solutioncalculate the gravitaional intensity and graviational potential at a location which is from the surface of the Earth at a height `4` times the radius of the surface. `R_(e) = 6400 km`,
`G = 6.67 xx 10^(-11) Nm^(2) kg^(-2) , M_(e) = 6 xx 10^(24) kg`.02:31View SolutionTwo masses of `500 kg` each are placed at two points `A` and `B`, distance `5 m` apart. There is a point `P` such that `AP = 3 m` and `BP = 4 m`. Find (i) the magnitude of gravitational intensity at `P` and
(ii) gravitational potential at `P`.
Given `G = 6.67 xx 10^(-11) Nm^(2) kg^(-2)`.05:52View SolutionWhat is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R?
02:33View SolutionA satellite of a mass `m` orbits the earth at a hight `h` above the surface of the earth. How much energy must be expended to rocket the satellite out of earth's gravitational influence? (where `M_(E)` and `R_(E)` be mass and radius of the earth respectively)
02:57View SolutionCalculate the gravitational potential energy of a body of mass `30 kg`, at a height of `4 R` from the surface of Earth, where `R (= 6.4 xx 10^(6) m)` is the radius of the Earth. Mass of the Earth `= 6.0 xx 10^(24) kg, G = 6.67 xx 10^(-11) Nm^(2) kg^(-2)`.
02:36View SolutionIn the solar system, the Sun is in the focus of the system for Sun-earth binding system. Then the binding energy for the system will be [given that radius of the earth's orbit round the Sun is `1.5 xx 10^(11) m` and mass of the earth `= 6 xx 10^(24) kg`]
01:56View SolutionAn artifical satellitee of mass `100 kg` is in a circular orbit at `500 km` above the Earth's surface. Take redius of Earth as `6.5 xx 10^(6) m`.(a) Find the acceleration due to gravity at any point along the satellite path (b) What is the centripetal acceleration o fthe satellite?
03:29View SolutionThe orbit of a geostationary satellite is concentric and coplanar with the equator of Earth and rotates along the direction of rotation of Earth. Calculate the height and speed. Take mass of Earth `= 6 xx 10^(-11) Nm^(2) kg^(-2)`. Given `pi^(2) = 10`.
03:48View SolutionAn Earth's satellite makes a circule around the Earth in `100` minutes. Calculate the height of the satellite above the Earth's surface. Given the radius of the Earth is `6400 km` `g = 10 ms^(-2)`. Use `pi^(2) = 10`.
05:40View SolutionThe radius of a planet is `R`. A satellite revolves around it in a circle of radius `r` with angular velocity `omega_(0)`. The acceleration due to the gravity on planet's surface is
01:24View SolutionThe escape speed of a body on the earth's surface is `11.2kms^(-1)`. A body is projected with thrice of this speed. The speed of the body when it escape the gravitational pull of earth is
03:54View SolutionA body is projected vertically upwards from the surface of the Earth so as to reach a height equal to the radius of the Earth. Neglecting resistance due to it, calculate the initial speed which should be imparted to the body. Mass of Earth `= 5.98 xx 10^(24) kg`, Radius of Earth `= 6400 km`, `G = 6.67 xx 10^(-11) Nm^(2) kg^(-2)`.
02:50View SolutionA spaceship is launched into a circular orbit close to the earth's surface . What additional velocity has now to be imparted to the spaceship in the orbit to overcome the gravitational pull. Radius of earth `= 6400 km`, `g = 9.8m//s^(2)`.
01:38View SolutionThe mass of the earth is `6.0 xx 10^(24) kg` and its radius is `6.4 xx 10^(6) m`. How much work will be done in taking a `10 kg` body from the surface of the Earth to infinity ? What will be the gravitational potential energy of the body on the Earth's surafce ?
`G = 6.67 xx 10^(-11) Nm^(2) kg^(-2)`.03:36View SolutionA body of mass `50 kg` falls on the earth from infinity. What will be its velocity on reaching the earth? What will be its `KE`? Take radius of the earth `= 6.4 xx 10^(6) m , g = 10 ms^(-2)`. Air friction is neglected.
02:45View SolutionFind the work done to bring `4` particle each of mass `100` gram from distances to the vertices of a square of side `20 cm`.
04:14View SolutionTwo masses, `800 kg` and `600 kg` are at a distance `0.25 m` apart. The magnitude of total force experienced by a body of mass `1 kg` placed at a point distance `0.2 m` from the `800 kg` mass and `0.15 m` from the `600 kg` mass :
05:59View SolutionInfinite number of masses, each of mass `m`, are placed along a straight line at distance of `r, 2r, 4r, 8r`, etc. from reference point `O`. Find the
(i) gravitational field intensity and
(ii) gravitational potential at point `O`.04:59View SolutionIn an imaginary planetary systam, the centrel star has the same mass as our sun, but is much brighter so that only a planet twice the distance between the Earth and sun can support life. According to bilogical evolution (including aging processes etc.) on that planet similar to ours, what would be the average life span of a 'human' on that planet in terms of its natural life ? The average life span of a human on the Earth may be taken to be `70` years.
03:49View Solution
PROBLEMS FOR PRACTIVE questions and complete solutions for chapter GRAVIATION of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS GRAVIATION
- ADDITIONAL EXERCISES
- ADVANCED PROBLEMS FOR COMPETITIONS
- Assertion-Reason Type Questions
- CONCEPTUAL PROBLEMS
- CONCEPTUAL PROBLEMS I.
- CONCEPTUAL PROBLEMS II.
- CONCEPTUAL PROBLEMS III.
- CONCEPTUAL PROBLEMS IV.
- CONCEPTUAL PROBLEMS V.
- CURIOSITY QUESTION
- FILL IN THE BLANKS
- FOCUS Multiple Choice questions I.
- Integer Type Questions
- LONG ANSWER QUESTIONS
- MULTIPLE CHOICE QUESTIONS
- MULTIPLE CHOICE QUESTIONS -II
- Multiple Choice questions II.
- Multiple Choice questions III.
- Multiple Choice questions IV.
- Multiple Choice questions V.
- NCERT
- NCRET MULTIPLE CHOICE QUESTIONS -I
- PROBLEMS FOR PRACTIVE
- PROBLEMS FOR PRACTIVE A
- PROBLEMS FOR PRACTIVE B
- PROBLEMS FOR PRACTIVE C
- PROBLEMS FOR PRACTIVE D
- PROBLEMS FOR PRACTIVE E
- PROBLEMS FOR PRACTIVE F
- PROBLEMS FOR PRACTIVE G
- PROBLEMS FOR PRACTIVE H
- PROBLEMS FOR PRACTIVE I
- PROBLEMS FOR PRACTIVE J
- PROBLEMS FOR PRACTIVE K
- QUESTIONS
- Sample Problem
- SHORT ANSWER QUESTIONS
- SHORT ANSWER QUESTIONS I.
- SHORT ANSWER QUESTIONS II.
- SHORT ANSWER QUESTIONS III.
- SHORT ANSWER QUESTIONS IV.
- SHORT ANSWER QUESTIONS V.
- SOLVED EXAMPLES
- SOLVED EXAMPLES TYPE A
- SOLVED EXAMPLES TYPE B
- SOLVED EXAMPLES TYPE C
- SOLVED EXAMPLES TYPE D
- SOLVED EXAMPLES TYPE E
- SOLVED EXAMPLES TYPE F
- SOLVED EXAMPLES TYPE G
- SOLVED EXAMPLES TYPE H
- SOLVED EXAMPLES TYPE I
- SOLVED EXAMPLES TYPE J
- SOLVED EXAMPLES TYPE K
- VALUE BASED QUESTIONS
- VERY SHORT ANS. QUESTIONS
- VERY SHORT ANS. QUESTIONS I.
- VERY SHORT ANS. QUESTIONS II.
- VERY SHORT ANS. QUESTIONS III.
- VERY SHORT ANS. QUESTIONS IV.
- VERY SHORT ANS. QUESTIONS V.
- VERY SHORT ANSWER QUESTIONS
