Complete Solutions to ADDITIONAL EXERCISES of chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEMS OF PARTICLES AND ROTATIONAL MOTION |
| PRADEEP | ADDITIONAL EXERCISES |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
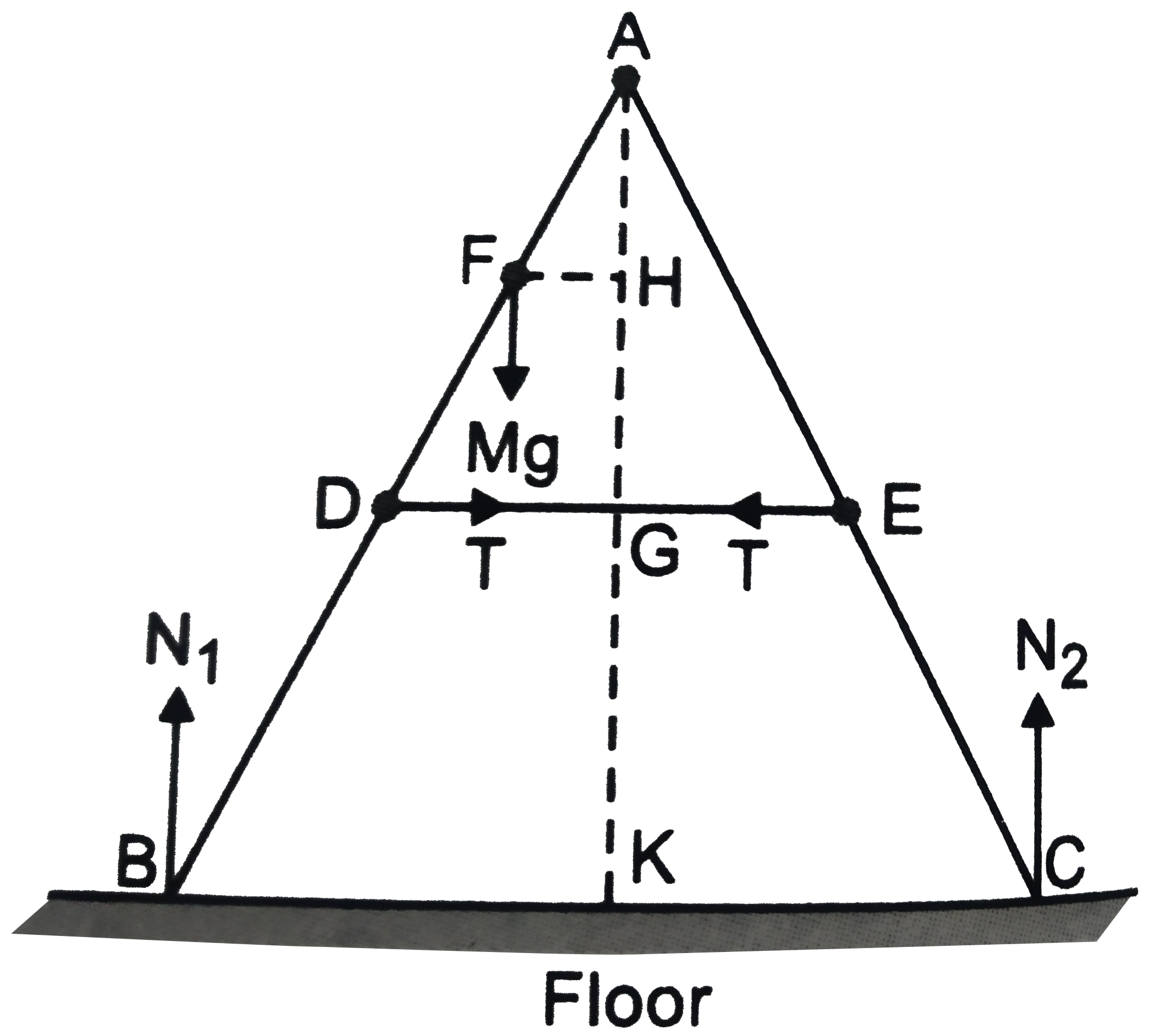
As shown in Fig. the two sides of a step ladder `BA` and `CA` are `1.6 m` long and hinged at `A`. A rope `DE, 0.5 m` is tied half way up. A weight `40 kg` is suspended from a point `F, 1.2 m` from B along the ladder` BA`. Assuming the floor to be fricionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take `g = 9.8 m//s^(2))`
(Hint. Consider the eqilibrium of each side of the ladder separately.)
 09:04View Solution
09:04View SolutionA man stands on a rotating platform, with his arms stretched horizontal holding a `5 kg` weight in each hand. The angular speed of the platform is `30` revolutions per minute. The man then brings his arms close to his body with the distance of each weight from the axis changing from `90 cm` to `20 cm`. moment of inertia of the man together with the platform may be taken to be constant and equal t `7.6 kg m^(2)`. (a) What is the his new angular speed ? (Neglect friction.)
(b) Is kinetic energy conserved in the process ? If not, from where does the change come about ?04:49View SolutionA bullet of mass `10 g` and speed `500 m//s` is fired into a door and gets embedded exactly at the centre of the door. The door is `1.0 m` wide and weight `12 kg`. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.(Hint. The moment of inertia of the door about the vertical axis at one end is `ML^(2)//3)`
06:12View SolutionTwo discs of moments of inertia `I_(1) and I_(2)` about their respective axes (normal to the disc and passing through the centre) and rotating with angular speeds `omega_(1) and omega_(2)` are brought into contact face to face with their axes of rotation coincident.
(a) Does the law of conservation of angular momentum apply to the situation ? Why ?
(b) Find the angular speed of the two-disc system.
(c ) Calculate the loss in kinetic energy of the system in the process.
(d) Account for this loss.08:40View Solution(a) Prove the theorem of perpendicular axes.
(Hint : Square of the distance of a point (x, y) in the x-y plane from an axis through the origin and perpendicular to the plane is `(x^(2)+y^(2))`.
(b) Prove the theorem of parallel axes.
(Hint : If the centre of mass of a system of n particles is chosen to be the origin `summ_(i)r_(i)=0`).05:39View SolutionProve the result that the velocity `v` of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclied plane of a hight h is given by `v^(2) = (2gh)/((1 + k^(2)//R^(2))` using dynamical consideration (i.e. by consideration of forces and torque). Note k i sthe radius of gyration of the body about its symmentry axis, and `R` is the radius of the body. The body starts from rest at the top of the plane.
06:03View SolutionA disc roating about its axis with angular speed `omega_(0)` is placed lightly (without any translational pull) on a perfectly frictionless table. The radius of the disc is `R`. What are the linear velocities of the points `A, B and C` on the disc shown in Fig. Will the disc roll in the direction indicated ?
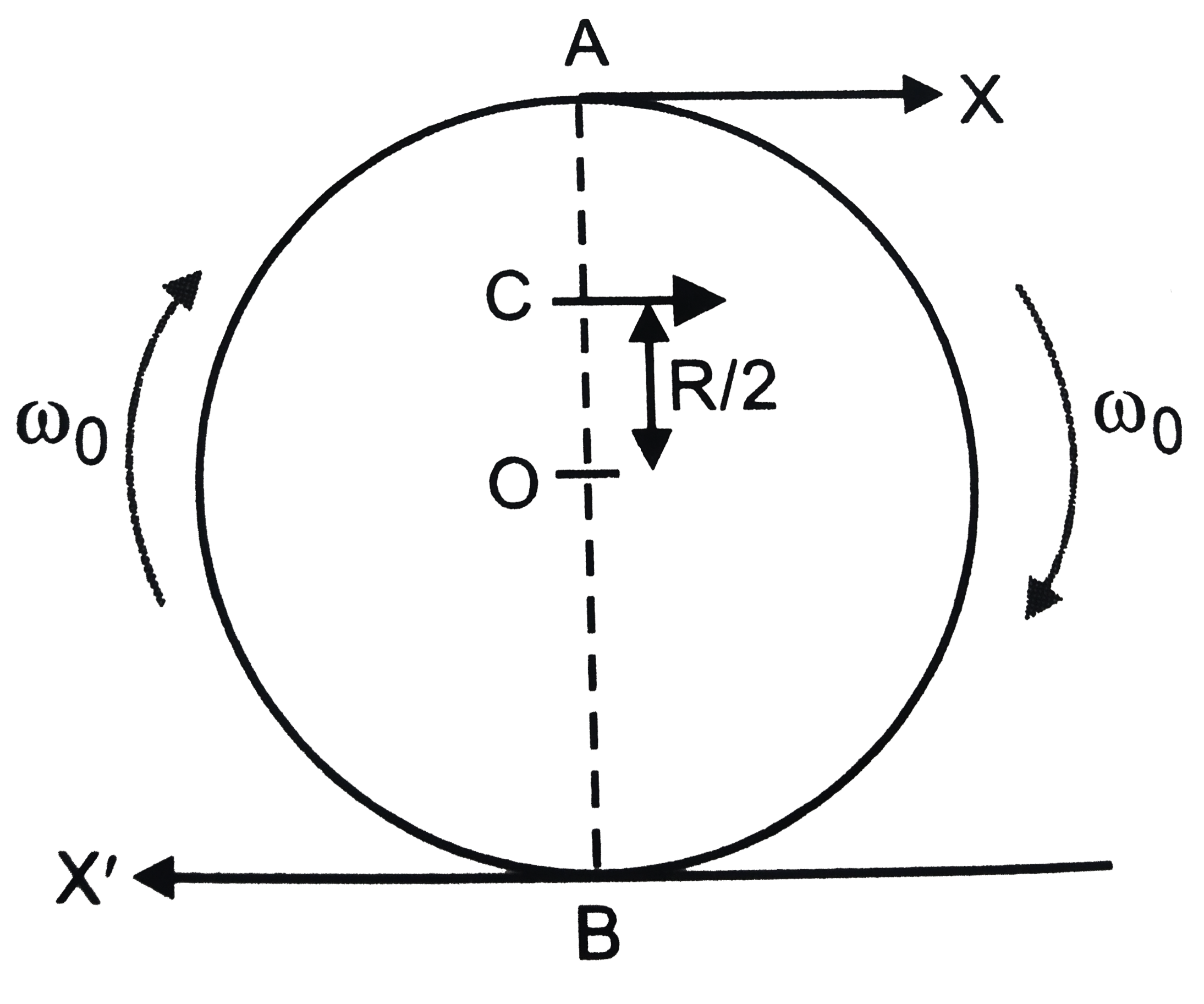 04:24View Solution
04:24View Solution(i) Explain why friction is necessary to make the disc to roll in the direction indicated. (ii) Give the direction of frictional force at `B`, and the sense of frictional torque, before perfect rolling begins. (iii) What is the force of friction after perfect rolling begins?
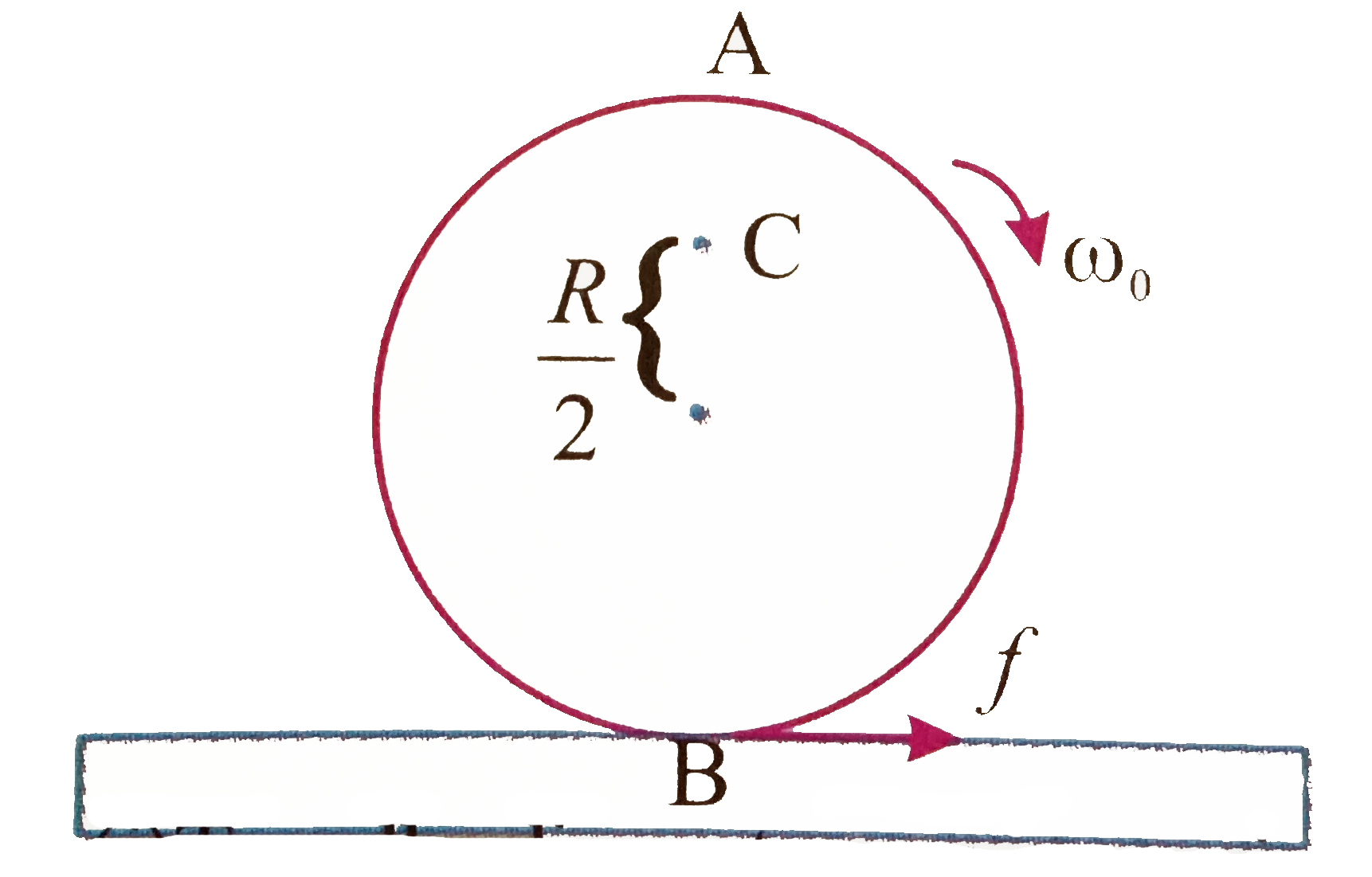 02:50View Solution
02:50View SolutionA solid disc and a ring, both of radius `10 cm` are placed on a horizontal table simultaneously, with initial angular speed equal to `10 pi rad//s`. Which of the two will start to roll earlier ? The coefficient of kinetic friction is `mu_(k) = 0.2`.
14:09View SolutionA cylinder of mass `10 kg` and radius `15 cm` is rolling perfectly on a plane of inclination `30^(@)`. The coefficient of static friction is `mu_(s) = 0.25`.
(a) How much is the force of friction acting on the cylinder ?
(b) What is the work done against friction during rolling ?
(c ) If the inclination `theta` of plane is increased, at what value of `theta` does the cylinder begin to skid and not roll perfectly ?07:58View SolutionRead each statement below carefully and state with reasons, if it is true ot false. (a) During rolling the force of friction acts in the same direction as the direction of motion of c.m of the body. (b) The instantaneous speed of the point of contact during rolling is zero. (c ) The instantaneous acceleration of the point of contact during rolling is zero. (d) For perfect rolling motion, work done against friction is zero. (e) A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling motion).
09:58View Solution
ADDITIONAL EXERCISES questions and complete solutions for chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- ADDITIONAL EXERCISES
- ADVANCED PROBLEMS FOR COMPETITIONS
- Assertion- Reason Type questions
- CONCEPTUAL PROBLEMS
- CONCEPTUAL PROBLEMS I.
- CONCEPTUAL PROBLEMS II.
- CURIOSITY QUESTIONS
- FILL IN THE BLANKS
- Focus Multiple Choice Questions I.
- Integer Type Questions
- LONG ANSWER QUESTIONS
- MULTIPLE CHOICE QUESTIONS
- Multiple Choice Questions Comprehension 2
- Multiple Choice Questions II.
- Multiple Choice Questions III. Comprehension 1
- MULTIPLE CHOICE QUESTIONS-I
- MULTIPLE CHOICE QUESTIONS-II
- NCERT
- PROBLEMS FOR PRACTICE
- PROBLEMS FOR PRACTICE TYPE A
- PROBLEMS FOR PRACTICE TYPE B
- PROBLEMS FOR PRACTICE TYPE C
- PROBLEMS FOR PRACTICE TYPE D
- PROBLEMS FOR PRACTICE TYPE E
- QUESTIONS
- Sample problem
- SHORT ANSWER QUESTIONS
- SHORT ANSWER QUESTIONS I.
- SHORT ANSWER QUESTIONS II.
- SOLVED EXAMPLES
- SOLVED EXAMPLES TYPE A
- SOLVED EXAMPLES TYPE B
- SOLVED EXAMPLES TYPE C
- SOLVED EXAMPLES TYPE D
- SOLVED EXAMPLES TYPE E
- VALUE BASED QUESTIONS
- VERY SHORT ANSWER QUESTIONS
- VERY SHORT ANSWER QUESTIONS I.
- VERY SHORT ANSWER QUESTIONS II.
