Complete Solutions to EXERCISE of chapter INTRODUCTION TO THREE DIMENSIONAL GEOMETRY of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | INTRODUCTION TO THREE DIMENSIONAL GEOMETRY |
| MODERN PUBLICATION | EXERCISE |
| Number Of Questions | 86 |
| Academic Year | 2023-24 |
A point is on x-axis. What are its y-co-ordinate and z-co-ordinate ?
01:56View SolutionA point is in the XZ-plane. What can you say about its y-co-ordinate ?
01:30View SolutionIn the figure, find the reflection of P(x, y, z) in the: XY-plane.
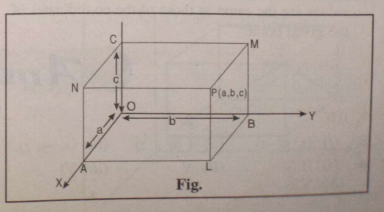 00:59View Solution
00:59View SolutionIn the figure, find the reflection of P(x, y, z) in the: YZ-plane.
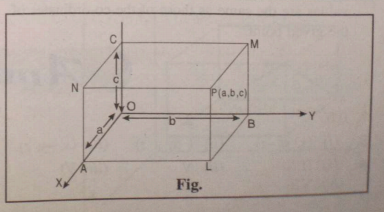 01:05View Solution
01:05View SolutionIn the figure, find the reflection of P(x, y, z) in the: ZX-plane.
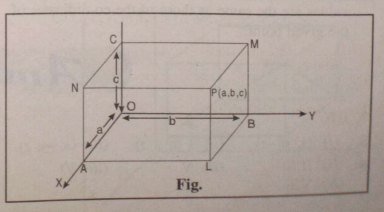 01:12View Solution
01:12View SolutionFind the octant in which the following points lie :
(- 3, 1, 2).01:43View SolutionFind the octant in which the following points lie :
(3, 1, - 2) .01:58View SolutionFind the octant in which the following points lie :
(- 3, 1, - 2) .01:43View SolutionFind the octant in which the following points lie :
(- 3, - 1, - 2).01:51View SolutionWrite the perpendicular distance of the point (x, y, z) from the three co-ordinate planes. (Assume that x, y, z are all positive)
02:46View SolutionThe co-ordinates of a point are (1, -2, 7). Find the co-ordinates of the seven points whose absolute values are the same as those of the co-ordinates of the given point.
02:53View SolutionWrite the co-ordinates of the feet of perpendicular from the point (a, b, c) on the co-ordinate axes.
01:41View SolutionFind the image of the point in the specified plane :
(5,4,-3) in the XY-plane.01:18View SolutionFind the image of the point in the specified plane :
(-2,0,0) in the XY-plane.01:02View SolutionFind the image of the point in the specified plane :
(-3, 4, 7) in the YZ-plane.01:08View SolutionFind the image of the point in the specified plane :
(- 7, 2, -1) in the ZX-plane.01:31View SolutionFind the image of the point in the specified plane :
(- 4,0, 1) in the ZX-plane.02:25View SolutionFind the perpendicular distances of the point P (a, b, c) from the co-ordinate axes.
04:22View SolutionPlanes are drawn parallel to co-ordinate planes through the points (3, 0, -1) and (-2, 5, 4). Find the lengths of the edges of the parallelopiped so formed.
04:13View SolutionFill in the blanks :
The x-axis and y-axis, taken together, determine a plane, known as ........ .01:02View SolutionThe co-ordinate of points in the xy-plane are of the form ……..
01:16View SolutionCo-ordinate planes divide the space into …….. Octants.
01:12View SolutionFind the distance between the points :
(1, -3,4) and (- 4, 1, 2) .01:44View SolutionFind the distance between the points :
(- 3,7,2) and (2, 4, - 1) .01:37View SolutionFind the distance between the points :
(- 1,3, - 4) and (1, - 3, 4) .01:37View SolutionFind the distance between the points :
(2,-1,3) and (- 2,1,3).02:29View SolutionFind the equation of the set of points which are equidistant from the points (1, 2, 3) and (3, 2, - 1).
05:00View SolutionFind the locus of a point, which is equidistant from the points (-1, 2, 3) and (3, 2, 1).
04:49View SolutionFind the locus of a point, which moves so that its distance from (1, 2, 3) is four times its distance from YZ-plane.
04:35View SolutionFind the points on the X-axis, which are at a distance of `2 sqrt6` units from the point (1,-2, 3).
05:43View SolutionFind the co-ordinate of a point on y-axis which are at a distance of `5sqrt(2)` from the point P(3,-2,5).
02:23View SolutionFind k so that the distance between the points (7, 1, - 3) and (4,5, k) be 13 units.
02:58View SolutionProve that the following points are collinear :
(- 2, 3, 5), (1, 2, 3), (7, 0, - 1).03:49View SolutionProve that the following points are collinear :
(2, - 1, 3), (4, 3, 1), (3, 1, 2).03:12View SolutionProve that the following points are collinear :
(6, - 7, - 1), (2, - 3, 1), (4, -5, 0).02:52View SolutionProve that the following points are collinear :
(- 1, 4, - 2), (2, -2, 1), (0, 2,-1).03:20View SolutionProve that the following points are collinear :
(3,-5,1), (-1, 0, 8), (7,-10, - 6).03:28View SolutionProve that the following points are collinear :
(2,- 4,1), (4, 4, 3), (3, 0, 2).03:21View SolutionProve that the following points are collinear :
(4, 5, - 5), (0, - 11, 3), (2, - 3, -1).03:29View SolutionProve that the following points are collinear :
(1, 2, 3), (4, 0, 4), (-2, 4, 2).04:24View SolutionProve that the following points are collinear :
(- 2, 3, 5), (1, 2, 3), (7, 0, - 1).03:49View SolutionVerify that the points (3, - 2, 4), (1, 0, - 2) and (-1,2, - 8) are collinear.
02:55View SolutionShow that the triangle with vertices (0, 7, 10), (-1, 6, 6) and (- 4, 9, 6) is right-angled.
03:29View SolutionAre the points A (3, 6, 9), B (10, 20, 30) and C (25,- 41, 5) the vertices of a right-angled triangle ?
04:03View SolutionProve that the points (0, 7,-10), (1, 6,-6) and (4,9, - 6) are the vertices of an isosceles triangle.
03:11View SolutionShow that A(a,b,c),B(b,c,a) and C(c,a,b) are the vertices of an equilateral triangle.
03:15View SolutionShow that the points : (0,4,1),(2,3,-1),(4,5,0) and (2,6,2) are vertices of square.
05:28View SolutionShow that the points `(1, 2, 3), (-1, -2, -1), (2, 3, 2) and (4, 7, 6)` are the vertices of a parallelogram.
08:04View SolutionShow that the points (-1,2,1), (1,-2,5), (4,-7,8) and (2,-3,4) are vertices of a parallelogram.
04:45View SolutionShow that the points (5, - 1, 1),(7, - 4, 7), (1, - 6, 10) and (- 1, -3, 4) are the vertices of a rhombus.
06:03View SolutionFind the equation of the set of points P, the sum of whose distance from A(4,0,0) and B(-4,0,0) is equal to 10.
05:43View SolutionIf A and B be the points (3,4,5) and (-1,3,-7) respectively, find the equation of the set of point P such that `PA^2+PB^2=k^2`, where k is constant.
04:57View SolutionFind the co-ordinates of the point, which is equidistant from four points (0, 0, 0), (a, 0, 0), (0, b, 0) and (0, 0, c).
04:09View SolutionFind the co-ordinates of the point, which is equidistant from four points (0, 0, 0), (a, 0, 0), (0, b, 0) and (0, 0, c).
04:09View SolutionShow that (-1, 4, -3) is the circumcentre of the triangle formed by the points (3, 2, -5), (-3, 8, -5) and (- 3, 2, 1).
01:38View SolutionFind the co-ordinates of the point, which divides the join of (-2, 3, 5) and (1, - 4, - 6) in the ratio 2 : 3 internally.
03:36View SolutionFind the co-ordinates of the point, which divides the join of (-2, 3, 5) and (1, - 4, - 6) in the ratio 2 : 3 externally.
02:41View SolutionFind the co-ordinates of the points, which divide the join of the points (1, -2, 3) and (3, 4, -5) in the ratio 2 : 3 internally.
02:22View SolutionFind the co-ordinates of the points, which divide the join of the points (1, -2, 3) and (3, 4, -5) in the ratio 2 : 3 externally.
02:29View SolutionFind the co-ordinates of the mid-point of the join of the points A (3, 5, 7) and B(-3,-3, 1).
01:26View SolutionFind the coordinates of the points which trisect the line segment joining the points P(4,2,-6) and Q(10,-16,6).
05:41View SolutionFind the co-ordinates of the point R, which divides the join of P (0, 0, 0) and Q (4, -1, -2) in the ratio 1 : 2 externally and verify that P is the mid-point of [RQ].
05:04View SolutionFind the ratio in which the line joining the points (- 2, 4, 5) and (3,- 5, 4) is divided by xz plane.
01:56View SolutionFind the ratio in which the line joining the points (- 2, 4, 5) and (3,- 5, 4) is divided by xz plane.
01:56View SolutionFind the ratio in which the line segment joining the points (4, 8, 10) and (6, 10, -8) is divided by yz-plane.
05:57View SolutionFind the ratio in which yz-plane divides the line segment formed by Joining the points (-2, 4, 7) and (3,-5, 8).
07:10View SolutionFind the ratio in which `2x+3y+5z=1` divides the line joining the points `(1, 0, -3) and (1, -5, 7).`
04:01View SolutionGiven that A (3, 2,-4), B(5, 4, -6) and C(9, 8, -10) are collinear. Find the ratio in which B divides [AC].
03:44View SolutionUsing Section formula, show that the points A (2,- 3, 4), B (-1, 2, 1) and C `(0,1/3,2)` are collinear.
02:55View SolutionGiven that p(3,2,-4) , Q (5,4, -6) and R (9,8,-10) are collinear find the ratio in which Q divides PR
02:14View SolutionIf the mid points of the sides of a triangle are `(1, 5, -1), (0, 4, -2) and (2, 3, 4).` Find its vertices.
08:48View SolutionShow that the points (-1,2,1), (1,-2,5), (4,-7,8) and (2,-3,4) are vertices of a parallelogram.
04:45View SolutionThree vertices of parallelogram ABCD are A(3,-1,2), B(1,2,-4), C(-1,1,2). Find the co-ordinate of the fourth vertex.
04:06View SolutionShow that the points A(1, 2, 3,), B (-1, -2. -1), C(2, 3, 2) and D(4, 7, 6) are the vertices of parallelogram ABCD but it is not a rectangle.
08:24View SolutionThe vertices of triangle are `A(1,1,2),B(4,3,1) and C(2,3,5)`. A vector representing the internal bisector of the `angleA` is
05:09View SolutionFind the lengths of the medians of the triangle A (0, 0, 6), B (0, 4, 0) and C (6, 0, 0).
03:24View SolutionThe centroid of a triangle ABC is at the point (1,1,1). If the coordinates of A and B are (3,-5,7) and (-1,7,-6) respectively, find the coordinats of the point C.
03:18View SolutionIf the origin is the centroid of the triangle PQR with vertices P(2a,2,6), Q(-4,3b,-10) and R(8,14,2c), then find the value of a,b and c.
02:52View SolutionPlanes are drawn through the points (5, 0, 2) and (3, - 2, 5) parallel to the co-ordinates planes. Find the lengths of the edges of the rectangular parallelopiped so formed.
01:32View SolutionProve that the lines joining the vertices of a tetrahedron to the centroids of the opposite faces are concurrent.
04:10View SolutionFind the lengths of the edges of the rectangular parallelopiped formed by planes drawn through the points (1, 2, 3) and (4, 7, 6) parallel to the co-ordinate planes.
01:44View SolutionVerify that (0, 7, 10) , (-1,6,6) and (-4, 9,6) are the vertices of a right angled triangle.
04:14View SolutionShow that the points : (4, 7, 8), (2, 3, 4), (- 1, - 2, 1), (1, 2, 5) are the vertices of a parallelogram.
04:08View SolutionShow that the points (5, - 1, 1),(7, - 4, 7), (1, - 6, 10) and (- 1, -3, 4) are the vertices of a rhombus.
06:03View SolutionIf A and B be the points (3,4,5) and (-1,3,-7) respectively, find the equation of the set of point P such that `PA^2+PB^2=k^2`, where k is constant.
04:57View SolutionFind the co-ordinates of the point, which is equidistant from four points (0, 0, 0), (a, 0, 0), (0, b, 0) and (0, 0, c).
04:09View Solution
EXERCISE questions and complete solutions for chapter INTRODUCTION TO THREE DIMENSIONAL GEOMETRY of MODERN PUBLICATION of Class 11
