Complete Solutions to EXAMPLE of chapter RELATIONS AND FUNCTIONS of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| MODERN PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
If A = {1, 2} and B = (3, 4, 5}, obtain `A xx B` and represent it graphically.
01:56View SolutionIf A : {1, 2} and B = {a, b, c}, obtain `A xx B` and represent it by an arrow diagram.
01:19View SolutionFind x and y, if (2x, x + y) = (6, 2).
00:33View SolutionLet A = {a, b}, B = {a, b, c}. What is`A xx B`?
00:37View SolutionIf `A xx B = {(p, q), (p, r), (m, q),(m, r)}`, find A and B.
00:37View SolutionLet A and B be two sets such that n (A) = 5 and n(B) = 2. If `(a_1, 2), (a_2, 3),(a_3,2), (a_4,3), (a_5,2)` are in `A xx B` and `a_1,a_2, a_3, a_4` and `a_5` are distinct, find A and B.
01:05View SolutionIf G = {7, 8} and H = {5, 4, 2}, find `G xx H` and `H xx G`.
02:34View SolutionIf P = {a, b,c } and Q= {r}, form the sets `P xx Q` and `QxxP`. Are these two Products equal ?
01:00View SolutionLet A and B be two sets such that n (A) = 5 and n(B) = 2. If a, b,c, d, e are distinct and (a, 2), (6, 3), (c, 2), (d, 3), (e, 2) are in `A xx B`, find A and B.
00:59View SolutionIf P = {1, 2}, form the set `P xx P xx P`.
01:20View SolutionLet A = {1, 2, 3, 4} and B = {5, 7, 9}. Determine : `A xx B` and represent it graphically.
02:44View SolutionLet A = {1, 2, 3, 4} and B = {5, 7, 9}. Determine : `B xx A` and represent it graphically.
03:02View SolutionLet A = {1, 2, 3, 4} and B = {5, 7, 9}. Determine : Is `A xx B= B xx A` ?
01:37View SolutionLet A = {1, 2, 3, 4} and B = {5, 7, 9}. Determine : Is `n(A xx B)= n(B xx A)` ?
01:51View SolutionLet A = {2, 4, 6} and B = {a, b}. Represent the following product by arrow diagram :
`A xx B`.02:18View SolutionLet A = {2, 4, 6} and B = {a, b}. Represent the following product by arrow diagram :
`B xx A` .01:58View SolutionLet A = {2, 4, 6} and B = {a, b}. Represent the following product by arrow diagram :
`A xx A` .02:06View SolutionLet A = {2, 4, 6} and B = {a, b}. Represent the following product by arrow diagram :
`B xx B` .00:43View SolutionIf A = { 1, 2}, B = {3, 4}, C = {4, 5}, find `A xx (B uu C)`.
00:59View SolutionLet A = {1, 2, 4}, B= {3, 5, 7} and C = {5, 7, 9}, find `A xx (B nn C)`.
01:02View SolutionLet A = {1, 2, 3}, B = {2, 3, 4} and C = {4, 5}. Verify that : `Axx(B nn C)=(AxxB)nn (A xx C)`.
02:52View SolutionLet `A ={1/2,2}`, B= {2, 3, 5}, C = {- 1, - 2}, then verify the following : `Axx (B uu C)=(AxxB) uu (AxxC)`.
04:02View SolutionLet `A ={1/2,2}`, B= {2, 3, 5}, C = {- 1, - 2}, then verify the following : `Axx (B - C)=(AxxB) - (AxxC)`.
03:06View SolutionFor any three sets A, B, C, prove that : `Axx(B nn C)=(A xx B)nn (Axx C)` .
04:03View SolutionFor any three sets A, B, C, prove that : `Axx(B - C)=(A xx B)- (Axx C)` .
04:15View SolutionFor any sets A, B, C, D , prove that: `(AxxB)nn (CxxD)=(A nn C)xx(B nn D)`.
03:41View SolutionDetermine the domain and range of the relation R defined by R = {(x, x + 5) : x `in` {0, 1, 2, 3, 4, 5}}.
02:35View SolutionLetA= {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a ,`b in A`, b is exactly divisible by a}. Find the range of R.
03:52View SolutionLetA= {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a ,`b in A`, b is exactly divisible by a}. Find the domain of R
03:06View SolutionLetA= {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a ,`b in A`, b is exactly divisible by a}. Find the range of R.
03:52View SolutionIf A ={4,9,16,25}, B = {1, 2, 3, 4} and R is the relation ‘‘is square of" from A to B, write down the set corresponding to R. Also find the domain and range of R.
02:19View SolutionIf R is a relation "is divisor of" from the set A = {1, 2, 3} to B = {4, 10, 15}, write down the set of ordered pairs corresponding to R.
01:06View SolutionLet R be the relation on the set N of natural numbers defined by a + 3b = 12. Find : R.
02:22View SolutionLet R be relation on the set N of natural numbers defined by a +3b=12 . Find : (i) R (ii) domain of R (iii) Range of R
05:10View SolutionLet R be relation on the set N of natural numbers defined by a +3b=12 . Find : (i) R (ii) domain of R (iii) Range of R
05:10View SolutionLet A = {1, 2} and B = {3, 4}. Find the number of relations from A to B.
01:27View SolutionIf R is the relation ‘lessthan from A={1,2,3,4,5} to B={1,4,5}. Write down the cartesion product corresponding to R. Also find the inverse relation to R.
03:25View SolutionLet A = {1, 2, 3, 4,5,6}. Define a relation R from A to A by : R = {(x, y): y= x +1}. Depict this relation by arrow diagram.
02:34View SolutionLet A = {1, 2, 3, 4,5,6}. Define a relation R from A to A by : R = {(x, y): y= x +1}. Write down the domain, co-domain and range of R.
02:48View SolutionThe figure given below shows the relationship between the sets P and Q.
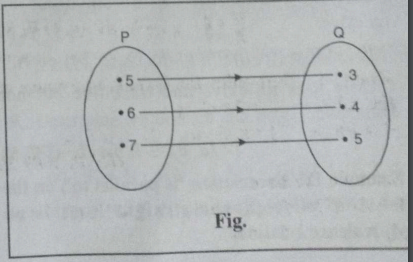 Write this relation in set builder form.`01:46View Solution
Write this relation in set builder form.`01:46View SolutionThe figure given below shows the relationship between the sets P and Q.
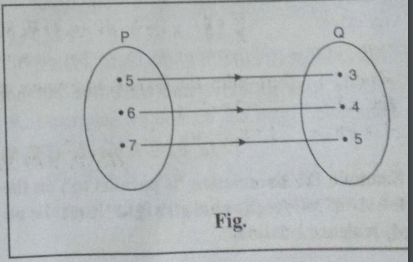 Write this relation in roster form.00:35View Solution
Write this relation in roster form.00:35View SolutionThe figure given below shows the relationship between the sets P and Q.
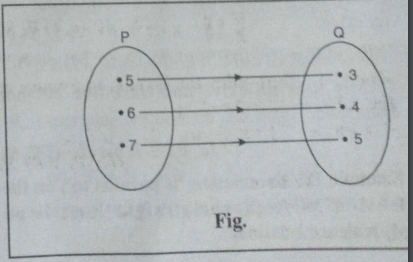 Write this relation What is its domain and range?00:56View Solution
Write this relation What is its domain and range?00:56View SolutionShow that the relation ‘>’ on the set R of all real numbers is transitive but it is neither reflexive nor symmetric.
04:21View SolutionConsider the set A = {a, b, c}. Give an example of a relation R on A. which is : reflexive and symmetric but not transitive.
02:41View SolutionConsider the set A = {a, b, c}. Give an example of a relation R on A. which is : Symmetric and transitive but not reflexive.
03:19View SolutionConsider the set A = {a, b, c}. Give an example of a relation R on A. which is : reflexive and transitive but not symmetric.
01:43View SolutionThe relation ‘is parallel to’, on the set A of all coplanar straight lines is an equivalence relation.
02:35View SolutionLet 'm' be a given positive integer. Prove that the relation, Congruence modulo m' on the set Z of all integers defined by : `a equiv b(mod m) hArr (a-b)` is divisible by m is an equivalence relation.
02:55View SolutionLet Z be the set of all integers and R be the relation on Z defined as `R = (a,b) : a,b `in` Z and a-b is divisible by 5) Prove that R is an equivalence relation.
06:32View SolutionIf R is a relation in `N xx N`, show that the relation R defined by (a, b) R (c, d) if and only if ad = bc is an equivalence relation.
03:24View SolutionWhich of the following graphs represent the function of x ? Why ?
 00:54View Solution
00:54View SolutionLet N be the set of natural numbers and the relation R be defined on N such that `R = {(x, y) : y = 2x, x, y in N}`. What is the domain, co-domain and Range of R ?
01:58View SolutionLet N be the set of natural numbers and the relation R be defined on N such that `R = {(x, y) : y = 2x, x, y in N}`. Is this relation a function ?
01:42View SolutionWhich of the following relations are functions ? Give reasons. If it is a function, determine its domain and range. R = {(2, 1), (3, 1), (4, 2), (5, 7), (6, 9)}.
01:41View SolutionWhich of the following relations are functions ? Give reasons. If it is a function, determine its domain and range. R = {(2, 2), (2, 4), (3, 3), (4, 4), (5, 8)}.
01:16View SolutionWhich of the following relations are functions ? Give reasons. If it is a function, determine its domain and range. R = {(1, 3), (1, 5), (2, 5), (3, 6), (3, 7)}.
01:16View SolutionLet f = {(1 ,1), (2, 3), (0, -1), (-1, -3)} be a linear function from Z into Z. Find f (x).
02:47View SolutionLet A = {1, 2, 3}, B= {4, 5} and let f = {(1, 4), (2, 5), (3, 5)}. Show that ‘f’ is an onto function from A into B.
02:16View SolutionLet N `rarr` N be defined by f (x) = 3x. Show that f is not an onto function.
02:12View SolutionLet A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Show that f is one-one.
02:52View SolutionIf `f (x) =x^3-1/x^3`, find the value of `f (x) +f (1/x)`.
01:10View SolutionIf ‘f’ is a real function defined by : `f(x)= (x-1)/(x+1)`, then prove that `f (2x) = (3 f(x)+1)/(f(x)+3)` .
02:11View SolutionIf `f (x) = 1/(2x+1), x ne -1/2`, then show that , `f(f (x)) = (2x+1)/(2x+3), x ne -3/2`.
01:38View SolutionIf `f (x) = log_e ((1+x)/(1-x))`, prove that: `f (x) +f (y)= f ((x+y)/(1+xy))` .
03:08View SolutionThe function ‘t', which maps temperature in Celsius into temperature in Fahrenheit is defined by `t(c)= (9c)/5+32`. Find : t(5 ).
00:41View SolutionThe function ‘t', which maps temperature in Celsius into temperature in Fahrenheit is defined by `t(c)= (9c)/5+32`. Find : t(25).
00:45View SolutionThe function ‘t', which maps temperature in Celsius into temperature in Fahrenheit is defined by `t(c)= (9c)/5+32`. Find : t(-5).
00:39View SolutionThe function ‘t', which maps temperature in Celsius into temperature in Fahrenheit is defined by `t(c)= (9c)/5+32`. Find : the value of c when t(c) = 210.
01:11View SolutionIf the function f : R `rarr` R is defined by , `f(x)= {(3x-1, if , x>3), (x^2-2, if , -2lexle3),(2x+3, if , xlt-2):}` Find : f (2).
01:09View SolutionIf the function f : R `rarr` R is defined by , `f(x)= {(3x-1, if , x>3), (x^2-2, if , -2lexle3),(2x+3, if , xlt-2):}` Find : f (4).
00:57View SolutionIf the function f : R `rarr` R is defined by , `f(x)= {(3x-1, if , x>3), (x^2-2, if , -2lexle3),(2x+3, if , xlt-2):}` Find : f(-1).
00:51View SolutionIf the function f : R `rarr` R is defined by , `f(x)= {(3x-1, if , x>3), (x^2-2, if , -2lexle3),(2x+3, if , xlt-2):}` Find : f(-3).
00:51View SolutionFor the relation `y = sqrtx` , say whether it is a function or not. If it is a function, find its domain and range.
02:53View SolutionFind the domain and range of the following functions : `f(x) = sqrt((x-1)(3-x))`.
03:06View SolutionFind the domain and range of the following function : `f (x) = 11-7 sin x`.
00:57View SolutionFind the domain and range of the following function : `f(x) = 1-|x|`.
01:59View SolutionFind the range of the following function : `f(x)= 1/((2x -3) (x +1))`.
03:42View SolutionFind the domain of the function `f(x) = (x^(2) + 3 x + 5)/( x^(2) - 5 x + 4)`
01:38View SolutionWhich of the following functions are odd or even or neither :
`f(x)=tanx+3" cosec "x+x`01:54View SolutionWhich of the following functions are odd or even or neither :
`f(x)=|x|+1`01:52View SolutionWhich of the following functions are odd or even or neither :
`f(x)=|x-2|`01:56View SolutionProve that f (x) =x-[x], where [x] denotes the integral part of x not exceeding and is periodic and find its period.
02:21View SolutionSolve : [2x- 3] = 5.
01:13View SolutionWhether the following relation is function? Give reason. If it is a function, determine its domain and range :
{(2, 1), (3, 1), (4, 2)}.01:19View SolutionWhich of the following relations are functions? Give reasons. If it is a function, determine its domain and range. `{(1,3), (1,5), (2,5)}.`
02:10View SolutionWhether the following relation is function? Give reason. If it is a function, determine its domain and range :
{(2, 2), (2, 4), (3, 3), (4, 4)}.01:01View SolutionWhich of the following relations are functions? Give reasons. If it is a function, determine its domain and range. `{(2,1), (5,1), (8,1), (11,1), (14,1), (17,1)}`
03:44View SolutionWhether the following relation is function? Give reason. If it is a function, determine its domain and range :
{(2, 1), (5, 1), (8, 1), (11, 2), (14, 2), (17, 2)}.01:29View SolutionWhether the following relation is function? Give reason. If it is a function, determine its domain and range :
{(1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7)}.01:37View SolutionWhether the following relation is function? Give reason. If it is a function, determine its domain and range :
{(2, 1), (4, 2),(6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}01:39View SolutionWhether the following relation is function? Give reason. If it is a function, determine its domain and range :
{(2, 1), (4, 2), (6, 3), (8, 4), (10, 5)}.01:30View SolutionWhether the following relation is function? Give reason. If it is a function, determine its domain and range :
{(1, 2), (2, 3), (3, 4), (3,5), (3, 7), (4,8)}.01:18View SolutionLet f = {(1,1), (2,3), (0,-1), (-1, -3)} be a function from Z to Z defined by `f(x) = ax + b`, for some integers a, b. Determine a, b.
03:39View SolutionDetermine function given below is one-to-one :
To each state of India assign its capital.01:53View SolutionDetermine function given below is one-to-one :
To each person on earth assign the number, which corresponds to his height.01:36View SolutionDetermine function given below is one-to-one : To each country in the world assign the latitude and longitude of its capital.
01:44View SolutionLet f: A `rarr` B be one-to-one function such that range of f is (b). Determine the number of elements in A.
00:59View SolutionIf `f(x) =3x^4-5x^2+7`, find f(x-1).
02:09View SolutionIf `f(x) =x^2-3x+4`, then find the values of x satisfying f (x) =f (2x+1).
02:19View SolutionIf `f(x) = x^2`, find `(f(1.1)-f(1))/((1.1-1))`.
02:23View Solution
EXAMPLE questions and complete solutions for chapter RELATIONS AND FUNCTIONS of MODERN PUBLICATION of Class 11
