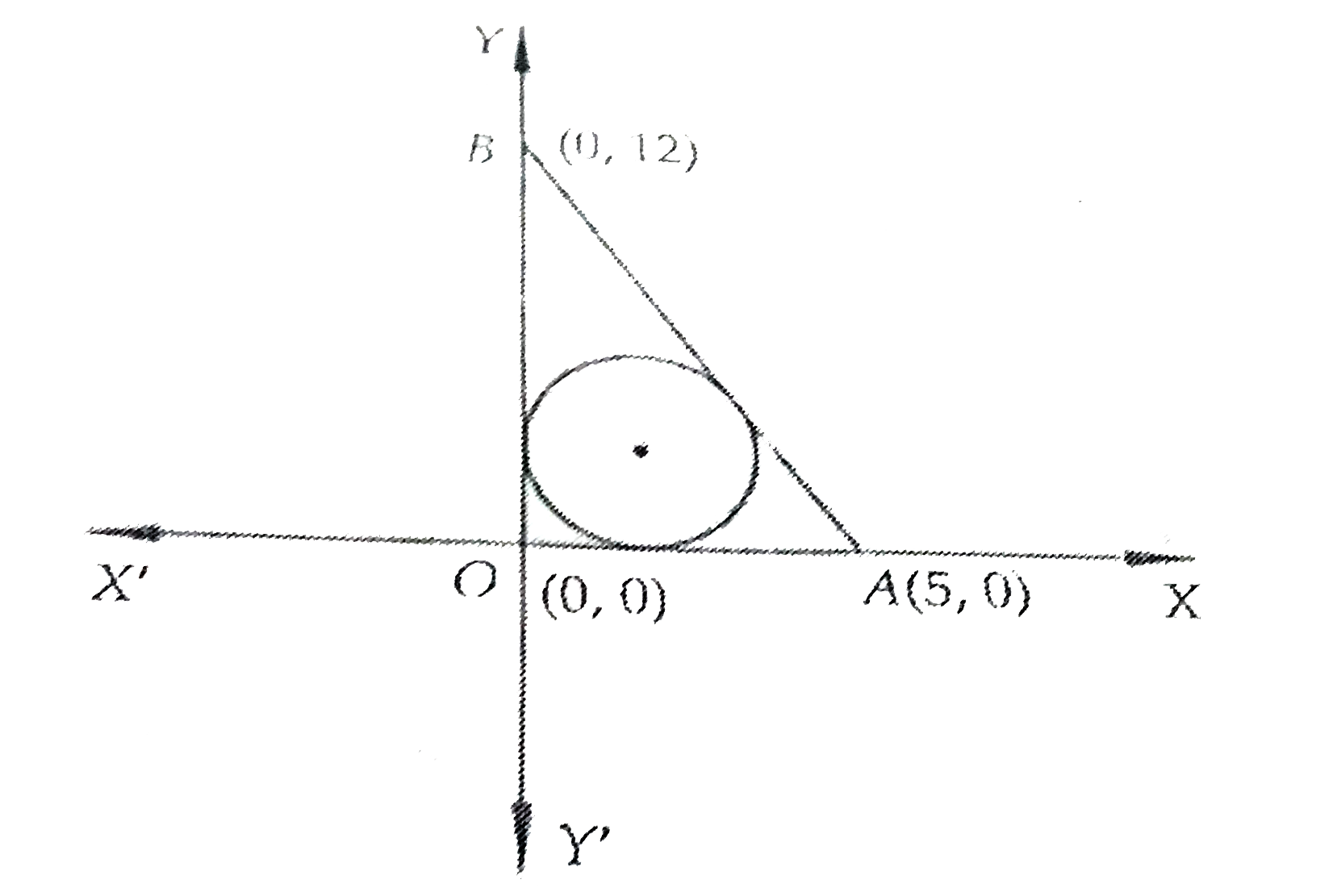
Write the coordinates of the incentre of the triangle having its vertices at (0,0), (5,0) and (0,12).
A
(3,3)
B
(2,2)
C
(7,7)
D
(9,9)
Video Solution
Text Solution
The correct Answer is:B
Clearly, ΔOAB is a rigth triangle right-angled at O such that OA,=5, OB=12 AB=13
So, the coordinartes of incentre are
(13×0+5×0+12×513+5+12,13×0+5×12+12×013+5+12) i.e., (2,2)
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN CO-ORDINATE SYSTEM EXERCISE - Section I - Solved Mcqs29videos
CARTESIAN CO-ORDINATE SYSTEM
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN CO-ORDINATE SYSTEM EXERCISE - Section II - Assertion Reason Type6videos
CARTESIAN CO-ORDINATE SYSTEM
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Chapter Test58videos
BINOMIAL THEOREM AND ITS APPLCIATIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DETERMINANTSEXERCISE - Chapter Test30videos
DETERMINANTS
Similar Questions
Knowledge Check
- Question 1 - Select One
The coordinates of the circumcentre of the triangle whose vertices are at (0,0),(6,0) and (0,8) is
A(a) (6,0)B(b) (0,8)C(c) (3,4)D(d) (0,0) - Question 2 - Select One
The coordinates of circumcentre of the triangle whose vertices are (0,0), (4,0) and (0,-6) is
A(0,0)B(4,0)C(0,−6)D(2,−3)
Find the co-ordinates of the orthocentre of a triangle whose vertices are (3,−1), (−1,2) and (0,0).
View SolutionFind the orthocentre of the triangle whose vertices are (0,0),(3,0), and (0,4).
View SolutionFind the orthocentre of the triangle whose vertices are (0,0),(3,0), and (0,4).
View SolutionFind the incentre of the triangle with vertices (1,√3),(0,0) and (2,0)
View SolutionThe incentre of the triangle whose vertices are (-36, 7), (20, 7) and (0, -8) is
View SolutionFind the coordinates of the centroid of a triangle whose vertices are (0, 6), (8, 12) and (8, 0) .
View Solution