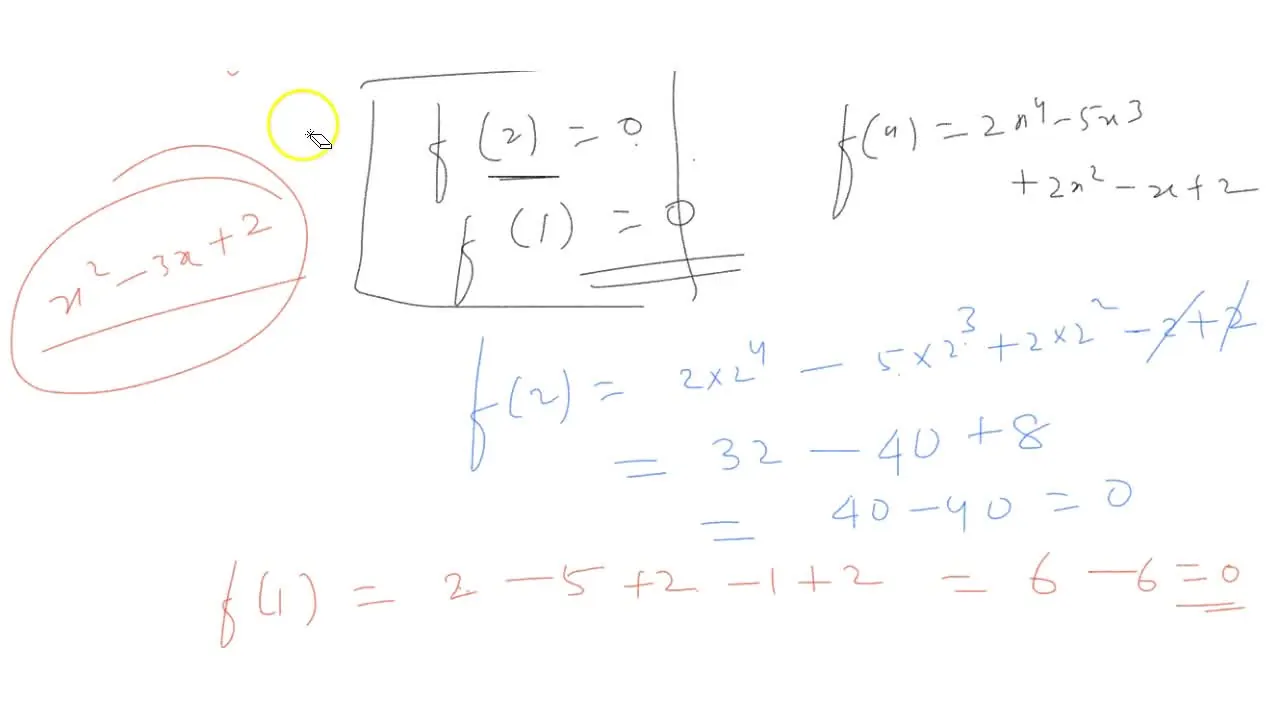Without actual division, prove that 2x4−5x3+2x2−x+2 is exactly divisible by x2−3x+2.
Let p(x)=2x4–5x3+2x2–x+2 firstly, factorise x2−3x+2.
Now, x2−3x+2=x2−2x−x+2 [by splitting middle term]
=x(x−2)−1(x−2)=(x−1)(x−2)
Hence, zeroes of x2−3x+2 are 1 and 2.
We have to prove that, 2x4–5x3+2x2–x+2 is divisible byx2−3x+2 i.e.,
to prove that p(1)=0 and p(2)=0
Now, p(1)=2(1)4–5(1)3+2(1)2−1+2=2−5+2−1+2=6−6=0
and p(2)=2(2)4–5(2)3+2(2)2–2+2=2x16−5x8+2x4+0=32–40+8=40–40=0
Hence, p(x) is divisible by x2−3x+2.
Related Playlists
Similar Questions
Without actual division, prove that 2x4−6x3+3x2+3x−2 is exactly divisible by x2−3x+2
View SolutionWithout actual division prove that 2x4−6x3+3x2+3x−2 is exactly divisible by x2−3x+2 is
View SolutionWithout actual division, prove that 2x4−5x3+2x2−x+2 is divisible by x2−3x+2.
View SolutionWithout actual division, prove that (2x4−6x3+3x+3x−2) is exactly divisible by (x2−3x+2).
View SolutionWithout actual division , prove that 2x4−5x3+2x2−x+2 is divisible by x2−3x+2.
View SolutionWithout actual division prove that 2x4−6x3+3x2+3x−2 is exactly division by x2−3x+2.
View SolutionWithout actual division, prove that x4+2x3−2x2+2x−3 is exactly divisible by x2+2x−3.
View SolutionWithout actual division , prove that (2x4+3x3−12x2−7x+6) is exactly divisible by (x2+x−6).
View SolutionWithout actual division, show that x3−3x2−13x+15 is exactly divisible by (x2+2x−3),
View SolutionProve that 2x4−9x3+21x2−26x+12 is completely divisible by 2x-3.
View Solution