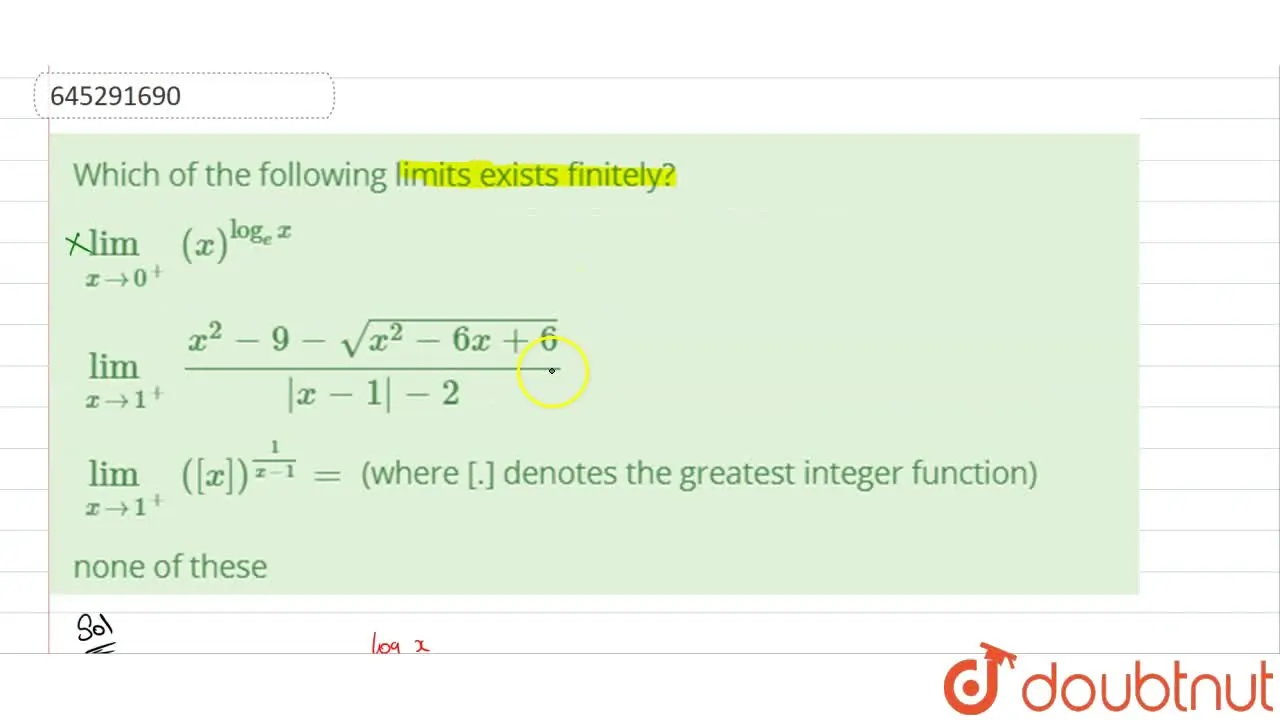
Which of the following limits exists finitely?Solution in Tamil
(where [.] denotes the greatest integer function)
none of these
The correct Answer is:C
(a)
So, limits does not exist finitely.
(b)
Now,
Also,
So, limit does not exist.
(c)
Related Playlists
- BOOK - CENGAGECHAPTER - LIMITSEXERCISE - Multiple Correct Answers Type4videos
LIMITS
- BOOK - CENGAGECHAPTER - LIMITSEXERCISE - ComprehensionType2videos
LIMITS
- BOOK - CENGAGECHAPTER - LIMITSEXERCISE - JEE Advanced Previous Year7videos
LIMITS
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 109videos
JEE 2019
- BOOK - CENGAGECHAPTER - LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSEXERCISE - DPP 1.210videos
LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORS
Similar Questions
If A=limx→0sin−1(sinx)cos−1(cosx)andB=limx→0[|x|]x, then
09:37View SolutionLet f(x) be the fourth degree polynomial such that f'(0)=−6,f(0)=2andlimx→1f(x)(x−1)2=1
The value of f(2) is04:17View SolutionIf limx→0[1+xln(1+b2)]1/x=2bsin2θ,b>0, and θ∈(−π,π], then the value of θ is
01:29View SolutionIf y = y(x) is the solution of the differential equation, xdydx+2y=x2 satisfying y(1) = 1, then y(12) is equal to
View SolutionThe number of integral values of p for which (p+1)ˆi−3ˆj+pˆk,pˆi+(p+1)ˆj−3ˆk and −3ˆi+pˆj+(p+1)ˆk are linearly dependent vectors is q
View SolutionWhich of the following has the limit as a finite number.
01:57View SolutionWhich of the following limit exists finitely? lim_(x rarr0^(+))(x)^(log_(e)x)
View SolutionWhich of the following limit exists?
07:03View SolutionWhich of the following qunatities related to an elcetron has a finite upper limit?
03:43View SolutionWhich of the following limits exists finitely?
01:46View Solutionनिम्नलिखित सीमाओं का निकालें यदि उनका अस्तित्व है।
limx→1[x]03:58View SolutionWhich of the following limits does not exist ?
01:01:15View SolutionWhich of the following limits exists finitely?
01:00:30View SolutionGeographic limit within which a population exists is called :
59:21View SolutionExamine the existence of the following limits:limx→0+logax
01:30:25View SolutionExamine the existence of the following limits:limx→0 cosecx
01:18:19View Solution