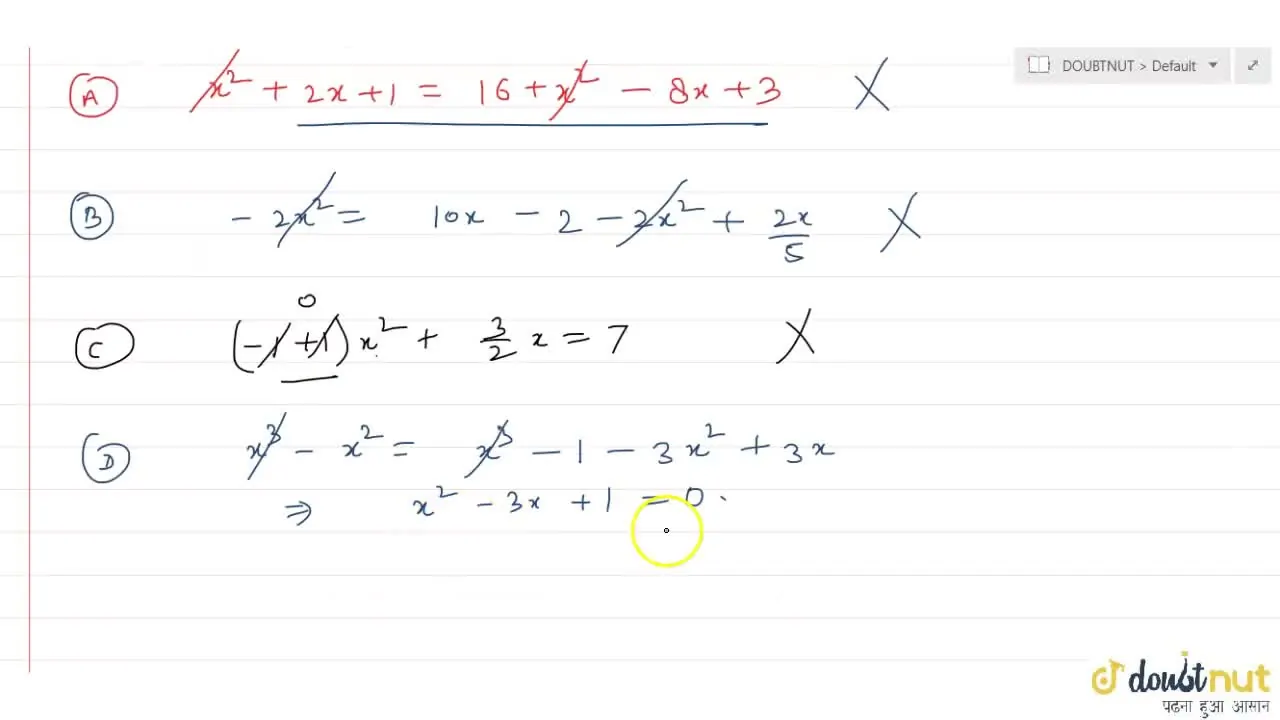Which of the following is a quadratic equation?
A
B
C
, where
D
Video Solution
Text Solution
The correct Answer is:D
(a) Given that
which is not of the form . Thus, the equation is not a quadratic equation.
(b) Given that
which is also not a quadratic equation
(c) Given that
Given
which is also not a quadratic equation.
(d) Given that
which represents a quadratic equation because it has the quadratic form
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Which of the following is quadratic equation ?
View SolutionWhich of the following are quadratic equations? x+3x=x2 (ii) x2+1x2=2
View SolutionWhich of the following are quadratic equations? x2−6x+4=0 (ii) 2x2−7x=0
View SolutionWhich of the following are quadratic equations? x−3x=x2 (ii) 2x2−√3x+9=0 (iii) x2−2x−√x−5=0
View SolutionWhich of the following are quadratic equations? x2+2√x−3=0 (ii) 3x2−4x+2=2x2−2x+4
View SolutionWhich of the following are quadratic equations? 3x2−5x+9=x2−7x+3 (ii) x+1x=1 (iii) x2−3x=0
View SolutionWhich of the following are quadratic equations? x2+6x−4=0 (ii) √3x2−2x+12=0 (iii) x2+1x2=5
View SolutionWhich of the following is not a quadratic equation ?
View SolutionWhich of the following is not a quadratic equation?
View SolutionWhich of the following is not a quadratic equation?
View Solution