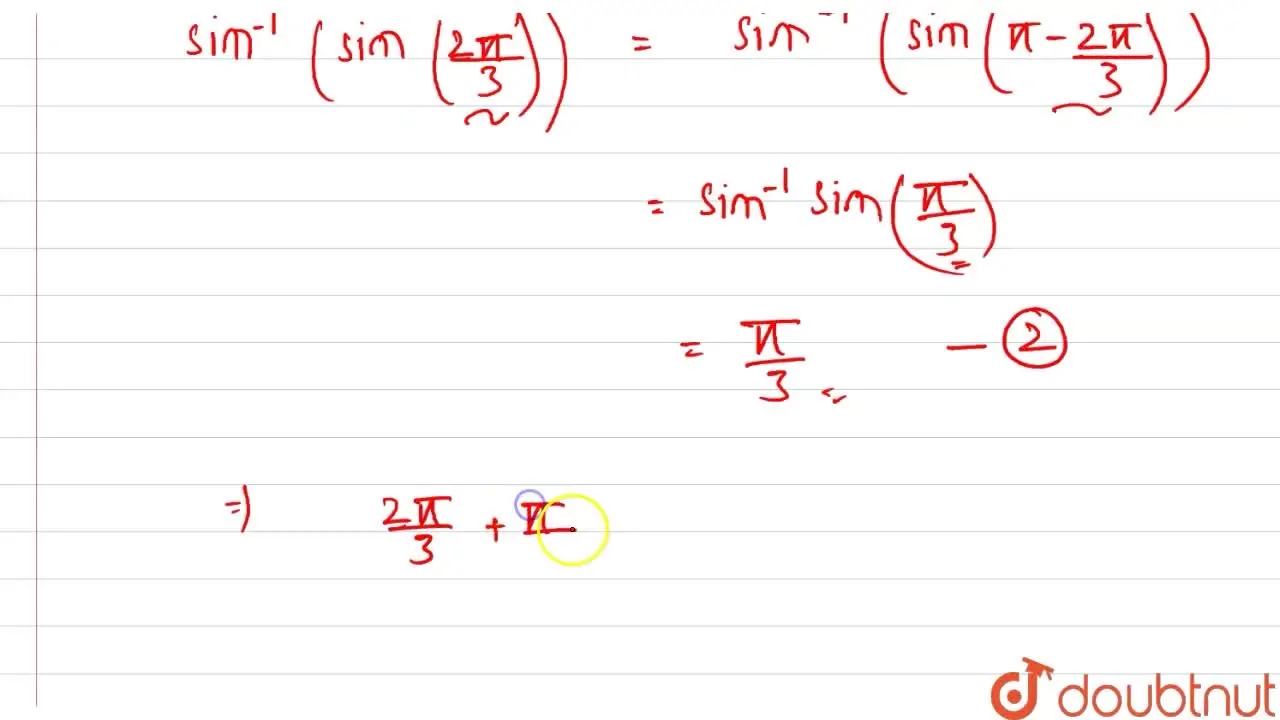What is the principal value of cos−1cos(2π3)+sin−1sin(2π3)?
Video Solution
Text Solution
cos−1cos(2π3)+sin−1sin(2π3)
We know, principal value of cos−1 is between 0 to 2π and for sin−1 is −π2 to π2.
∴ Principal value of cos−1cos(2π3)=2π3
sin−1sin(2π3)=sin−1sin(π−2π3)=sin−1sin(π3)=π3
∴ Principal value of sin−1sin(2π3)=π3
∴ Principal value of given expression =2π3+π3=π
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Write the principal value of cos−1(cos(2π)3)+sin−1(sin(2π)3)
View SolutionWrite the principal value of cos−1(cos(2π3))+sin−1(sin(2π3))
View SolutionWhat is the value of cos−1(cos(2π)3)+sin−1(sin(2π)3) ?
View SolutionThe principal values of cos−1(−sin(7π6)) is
View SolutionThe principal values of cos−1(−sin(7π)6) is
View SolutionFind the principal value of tan−1{cos(3π2)}
View SolutionThe value of cos−1(cos'3π2) is
View SolutionThe principal value of sin−1[cos(sin−1'12)] is
View SolutionThe principal value of sin−1[cos(sin−1'12)] is π3.
View SolutionFind the principal value of cos−1{sin[cos−1(12)]}
View Solution