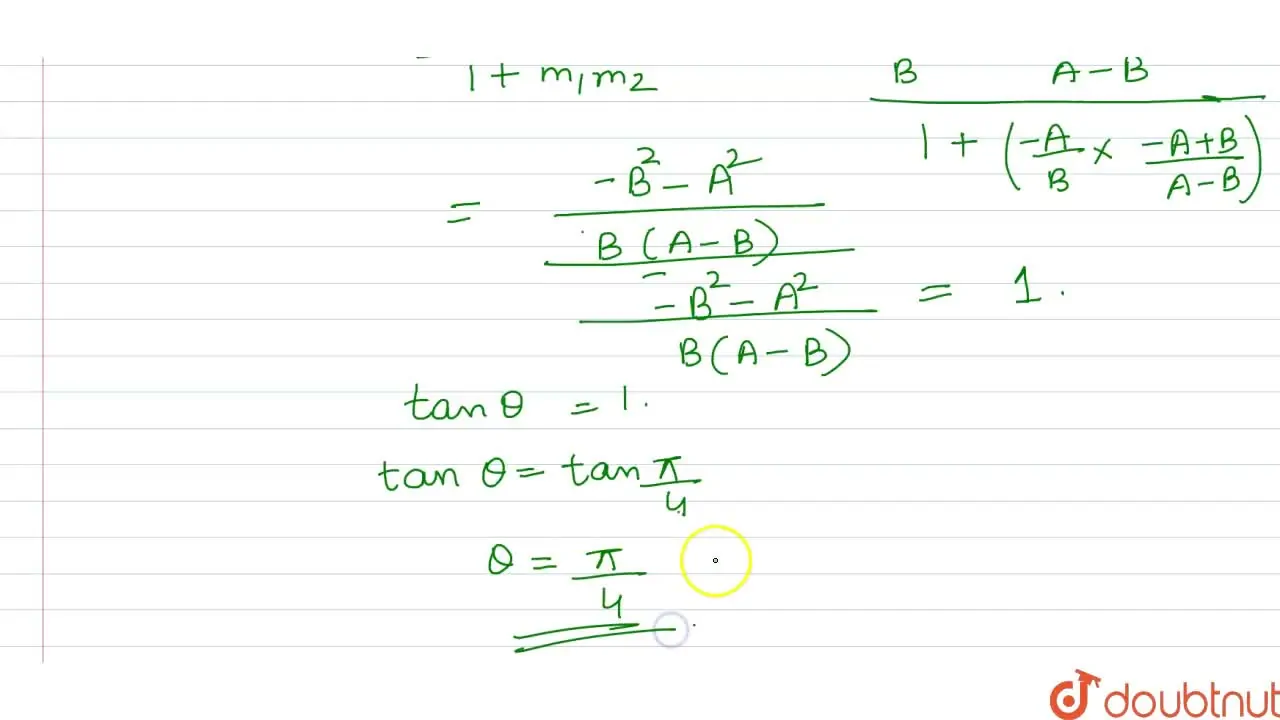What is the acute angle between the lines Ax+By=A+B and A(x−y)+B(x+y)=2B ?
Video Solution
Text Solution
The correct Answer is:A
Lines are L1≡Ax+By=A+B and
L2≡A(x−y)+B(x+y)=2B
Slope of L1 is −AB
m1=−AB [m1 is the side of line L1]
For line L2 :
Ax−Ay+Bx+By=2B
(A+B)x−(A−B)y=2B.
Slope of line L2 in (A+B)A−B
m2=(A+B)(A−B) [m2 is the slope of line L2]
If angle between line L1 and L2 is θ then
tanθ=m1−m21+m1m2
=−AB−A+BA−B1+(−AB)×(A+BA−B)=−A(A−B)−B(A+B)B(A−B)B(A−B)−A(A+B)B(A−B)
=−A2+AB−AB−B2AB−B2−A2−AB=−B2−A2−B2−A2=1
so, θ=π4
|
Updated on:21/07/2023
Related Playlists
Similar Questions
What is the acute angle between the lines Ax + By = A + B and A(x-y) + B(x+y) = 2 B ?
View SolutionWhat is the acute angle between the lines x−2=0 and √3x−y−2=0?
View SolutionWhat is the angle between the lines x+y=1 and x−y=1 ?
View SolutionFind the acute angle between lines x+y=0 and y=0
View SolutionWhat is the acute angle between the planes x+y+2z=3and−2x+y−z=11?
View SolutionWhat is the angle between the line x + y = 1 and x - y = 1 ?
View SolutionFind the acute angle between the lines 2x−y+3=0 and x+y+2=0.
View SolutionThe acute angle between the lines ax+by+c=0 and (a+b)x=(a−b)y,a≠b is
View SolutionIf θ is the acute angle between the lines given by ax2+2hxy+by2=0 then prove that tanθ=∣∣∣2√h2−aba+b∣∣∣. Hence find acute angle between the lines 2x2+7xy+3y2=0
View SolutionFind the acute angles between the st. Lines :
2x−y+3=0 and x+y−2=0View Solution