What is number system?
What is Number System?
In this chapter, we will study the number system. We will also look at the types of number system where you can also look forward to working on some number system questions.
What is the Number System?
The number system is used to state how many objects are there in a given set. The Roman numeral ‘I’ denotes the idea of ‘oneness’. The same thing is denoted by the Greek letter alpha ‘a’. It should be noted that alpha was the first letter which was used as a numeral. So, it is nothing but a Hindu-Arabic in origin. Let us study these in details.
In ancient Mesopotamia, the beginning system of the inscribed symbol was a system of symbols for numbers. You need to understand that the current number systems happen to be place-value systems. The place or position of the numbers determines the value of numbers in the representation. For example, the 4 in 40 and 400, which represents 4 ten’s and 4 hundred respectively. There was no positional characteristic in the ancient systems such as the Hebrew, Roman, Egyptian civilization and Greek number systems. So, it proved to be very complicated arithmetical calculations. But it can be mentioned that the principle of place value was used like the Mayan system.
The decimal positional number is the most commonly used number system. The decimal refers to the use of 10 numbers to construct all the required numbers like 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. The Indians discovered this where there are also two other common number systems. These are used in computing science and computers, which are the binary system that are denoted by ‘0’ and ‘1’. There are also hexadecimal system that has got 16 symbols which are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Types of Number System
We will now concentrate on the different types of number systems. Let us study in details:
Unary Numeral System
Unary Numeral System is the simplest number system of the numerals, where an equivalent number of symbols represents each and every natural number. Unary Numeral System is represented by /. Suppose, if we need to write 8, then it would be represented by //////// where we need to write eight /. Still in use in such system is the tally marks. However, it needs to be mentioned that when it comes to Unary Numeral System, it can only be used for numbers and that too of a smaller size as well. Still, it plays a vital role in the field of theoretical computer science
Binary Numeral System
When it comes to the Binary Numeral System, it is used in the world of science and in the system of mathematics. Here the expression of numbers is in the form of a base-2 system or binary numerical system. Here, only two numbers are used, which are 0’s (zeros) and 1’s (ones). It is based on the positional system in base 2 when it comes to the main system of number in computers. So, this is a binary numeral system that contains two digits of binary 0’s and 1’s. For example, in case of large numbers, bases 278 or 289 can be grouped in the binary digits by 78 or 89 as the portion of the machine world.
The Natural Numbers
The counting numbers from 1, 2, 3, 4, 5, 6, 7, 8, 9, etc. are the natural numbers. They are found to be infinite numbers where the set of the natural numbers is denoted by N in short. If there is an addition of any 2 natural numbers, it is also a natural number. For example, ( 6 + 3000) = 3006. Further, the outcome of the product of any two natural numbers is also a natural number. For example, (6 x 2500) = 15000. But if any two or more natural numbers are subtracted or divided, then they are not equal to natural numbers.
The Integers
The integers are the natural numbers that consist of the set of real numbers along with their additive inverses and zero.
{ …, -9, -8, -7, -6, -5 ,-4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6,7, 8, 9,…} The short form J or Z denotes the set of integers. It can also be represented on the number line. It is important to know that it can be decimal numbers or whole numbers. When any two integers are added or subtracted, the result value is also an integer, but this does not prove to be true for the division.
The Rational Numbers
Figures that can be formulated as a ratio between two integers are called the rational numbers. Any integer that can be written in the form of p/q is a rational number, where q is not equal to zero. All decimals which terminate are known as rational numbers. For example, 9.27 can be written as 927/100.
The Irrational Numbers
The numbers that cannot be written as a proportion or fraction are irrational numbers. In a decimal form, it does not end or neither repeats. It was discovered by the ancient Greek mathematician that not all integers are the rational number. Interestingly with the use of integers, some equations cannot be solved. For example, it is not possible to get the exact number by squaring the fraction or by terminating decimal numbers.
Identities for irrational numbers
Suppose a and b are real numbers then:
- √ab = √a√b
- (a+√b)(a−√b) = a²−b
- √ab = √a√b
- (√a+√b)(√c−√d) = √ac−√ad+√bc−√bd
- (√a+√b)(√c+√d) = √ac+√ad+√bc+√bd
- (√a+√b) (√a-√b) = a – b
- (√a+√b)2 = a+2√(ab)+b
The Real Numbers
The set of numbers that contain all the rational as well as irrational numbers are the real numbers. It consists of all the numbers on the number scale. They are also infinite numbers as well, where it is a bigger infinity. A unique real number is represented in every point on the line.
Expressing Decimals as rational numbers
Case 1 – Terminating Decimals
Example – 0.625
Let x=0.625
If the number of digits after the decimal point is y, then you need to multiply and divide the number by 10y.
Therefore, x = 0.625 × 1000/1000 = 625/1000 Next, you need to reduce the obtained fraction to its simplest form.
So, x = 5/8
Case 2: Recurring Decimals
In case the number is non-terminating and recurring, we will follow the following steps to convert it into a rational number:
__
Example – 1.042
Step1. Let x = 1.042 (1)
Step2. Now, multiply the first equation with 10y, where y is the number of recurring digits.
__
Therefore, 100x = 104.242
Steps 3. Now, you need to subtract equation 1 from equation 2.
So, we get99x = 103.2x=103.2/99 = 1032/990 , which is the required rational number.
Now, you need to reduce the obtained rational number to its simplest form.
Thus, x=172/165
Laws of Exponents for Real Numbers
Suppose a, b, m and n are real numbers then:
am × an= am+n
(am) n = amn
am/an = am−n
ambm=(ab)m
Here, a and b are the bases, and on the other hand, m and n are exponents.
Exponential representation of irrational numbers
Suppose a > 0 and n is a positive integer, then: n√a=a1n Let a > 0 be a real number and p and q be rational numbers, then:
ap × aq = ap + q
(ap)q = apq
ap/ aq= ap−q
apbp = (ab)p
The Complex Numbers
The set {a + bi } where the real numbers are a and b, the imaginary unit is i. √-1 The set of real numbers are included in the complex numbers where it includes the set of both rational and irrational numbers. In the complex system, the real numbers are denoted in the form of a + 0i = a, where a is a real number. In the short form, the set is always denoted by C.
Related Videos:
- Definition and representation of dfferent type of integers
- Decimal number system
- Rational number as recurring / terminating
- Number line and Its importance
- Representation of various types of no.s on no. line(natural no. integers rational nos)
We will work out on some problems to make it clearer to you.
Questions: Simplify the following:
(a) (8 + √5) (8 − √5)
(b) (10 + √3) ( 6 + √2)
(c) (√3 + √11)2 + (√3 - √11)2
Solutions:
(a) (8 + √5) (8 − √5)
The expression is of the form (x + y) (x – y) = x2 – y2
So, (8+√5) (8−√5) = (82−√52)
= 64 – 5 = 59
(b) (10 + √3) (6 + √2)
We need to expand the terms of the expression
= (10 × 6) + 10 × √2 + √3 ×6 + √2 ×√3
= 60 + √102 + √63 +√6
(c) (√3 + √11)2 + (√3 - √11)2
(√3 + √11)2 = (√3)2 + (√11)2 + 2 × √3 × √11
=3 + 11 + 2√33 = 14 + 2√33
(√3 - √11)2 = (√3)2 + (√11)2 - 2 × √3 × √11
=3 + 11 - 2√33 = 14 - 2√33
Therefore, (√3 + √11)2 + (√3 - √11)2 = 14 + 2√33 + 14 - 2√33
= 28.
Question: Rationalize the denominator
- 2 / √3−1
- 7 / √12−√5
- 1 / 8 + 3√5
Solutions:
- 2 / √3−1
The conjugate of (√3 – 1) is (√3 + 1)
2 / √3−1 x √3 + 1 / √3 + 1
= 2√3 + 1 / √32 - 12
= 2√3 + 1 / 3 - 1
= 2√3 + 1 / 2 = √3 + 1
(b) 7 / √12−√5
The conjugate of (√12 – 5) is (√12 + 5)
7 / √12−5 x √12 + √5 / √12 +√5
= 7√12 + √5 - √52 / √122
= 7√12 + √5 / 12- 5
= 7√12 + √5 / 12- 5 = √12 + √5
(c) 1 / 8 + 3√5
The conjugate of (8 + 3√5) is (8 + 3√5)
1 / 8 + 3√5 x 8-3 √5 / 8-3√5
= 8-3 √5 / 82 – (3√5)2
= 8-3 √5 / 64– 45
= 8-3 √5 / 19
Important Chapters:
(b) (10 + √3) ( 6 + √2)
(c) (√3 + √11)2 + (√3 - √11)2
Knowledge Check
- Question 1 - Select One
The binary system is a number system to the base
AA)2B2)4Cc)8DD)10 - Question 1 - Select One
In the Binary number system the number 100 represents :
AoneBthreeCfourDhundred - Question 1 - Select One
In the Binary number system 1+1=
A2B1C10D100
Similar Questions
Number Systems
View SolutionThe basic addition facts in the tens number system are given below :
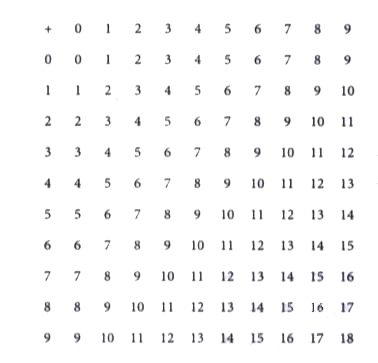
What is the order of the matrix by addition results ?View SolutionWhat is a river system?
View SolutionWhat do you understand by decimal number system and binary number system. Discuss conversion of decimal number system into binary number system with illustrations.
View SolutionThe base of the decimal number system is..........and the base of binary number system is.............
View SolutionThe number of digits in the Hindu-Arabic number system is____.
View SolutionWhat is 'Unitary system'?
View Solution

