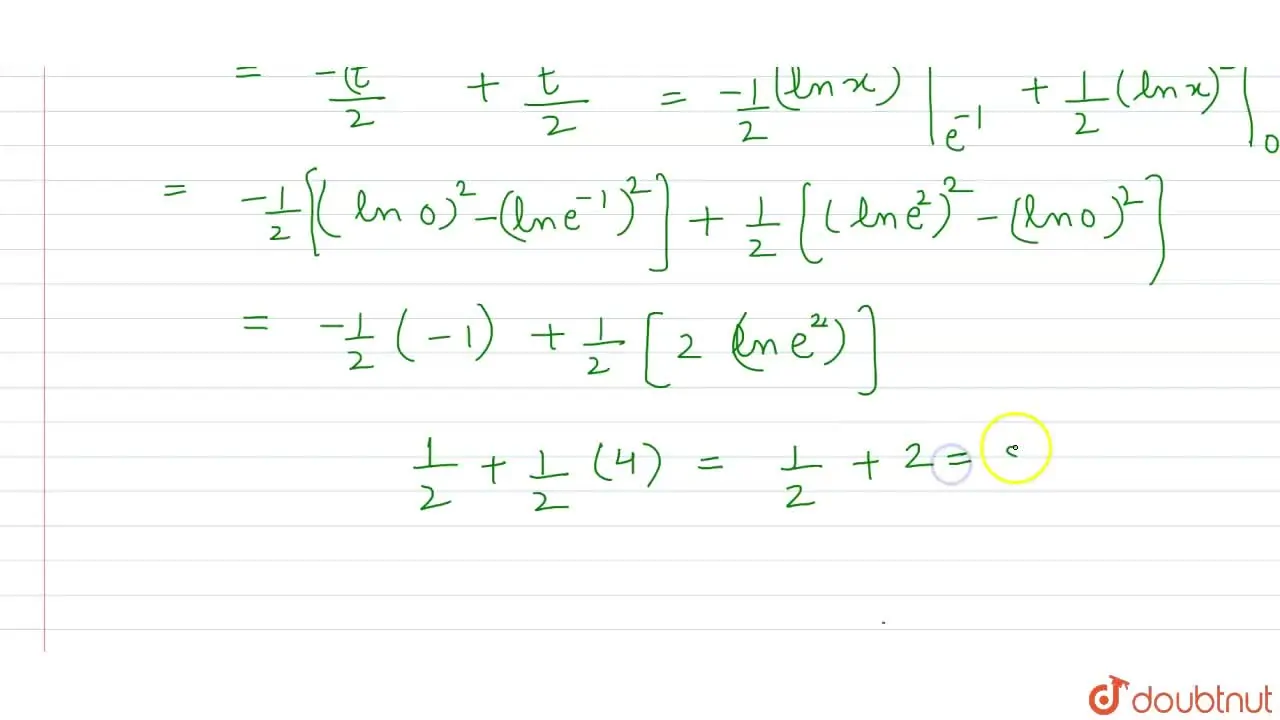What is |(ln x)/(x)|dx equal to ?
A
B
C
D
Video Solution
Text Solution
The correct Answer is:B
|
Updated on:21/07/2023
Related Playlists
- BOOK - NDA PREVIOUS YEARSCHAPTER - DEFINITE INTEGRATION & ITS APPLICATIONEXERCISE - DIRECTIONS60videos
DEFINITE INTEGRATION & ITS APPLICATION
- BOOK - NDA PREVIOUS YEARSCHAPTER - CONICS - PARABOLA, ELLIPSE & HYPERBOLAEXERCISE - MATH62videos
CONICS - PARABOLA, ELLIPSE & HYPERBOLA
- BOOK - NDA PREVIOUS YEARSCHAPTER - DERIVATIVESEXERCISE - MCQs94videos
DERIVATIVES
Similar Questions
∫e21lnx√xdx=
View Solution∫11e∣∣∣lnxx∣∣∣dx=
View Solution∫10dxex+e−xdx is equal to
View Solution∫e1ex(xlogex+1)xdx is equal to
View Solution∫ex(xlogx+1)xdx is equal to
View Solution∫e11+logxxdx=
View Solution∫e2elogxdx=
View Solution∫ln(ex+1)exdx
View Solution∫21logexx2dx
View Solution∫e11+logxxdx=
View Solution