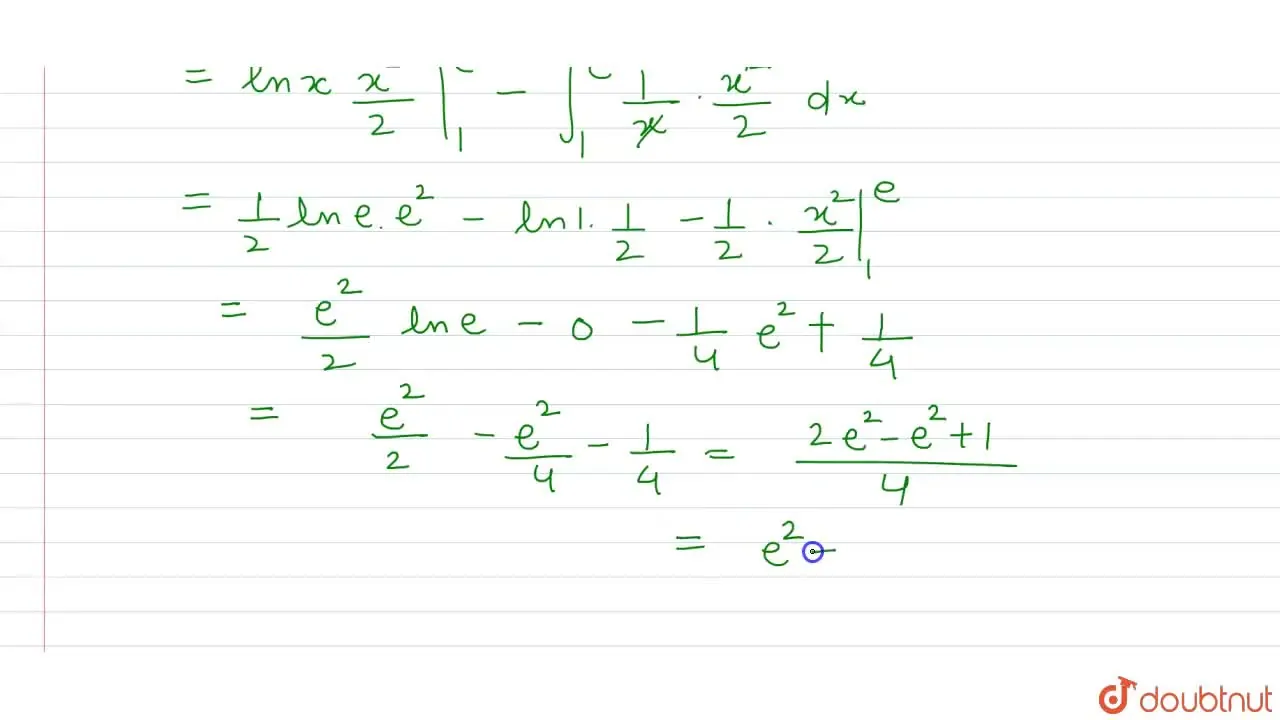What is equal to ?
A
B
C
D
Video Solution
Text Solution
The correct Answer is:B
|
Updated on:21/07/2023
Related Playlists
- BOOK - NDA PREVIOUS YEARSCHAPTER - DEFINITE INTEGRATION & ITS APPLICATIONEXERCISE - DIRECTIONS60videos
DEFINITE INTEGRATION & ITS APPLICATION
- BOOK - NDA PREVIOUS YEARSCHAPTER - CONICS - PARABOLA, ELLIPSE & HYPERBOLAEXERCISE - MATH62videos
CONICS - PARABOLA, ELLIPSE & HYPERBOLA
- BOOK - NDA PREVIOUS YEARSCHAPTER - DERIVATIVESEXERCISE - MCQs94videos
DERIVATIVES
Similar Questions
What is ∫e1xlnxdx equal to ?
View SolutionWhat is ∫20elnxdx equal to ?
View SolutionWhat is ∫1−1x|x|dxequal to ?
View Solution∫e11xdx is equal to
View SolutionWhat is ∫π0exsinxdx equal to ?
View SolutionWhat is ∫31∣∣1−x4∣∣dx equal to ?
View SolutionWhat is ∫10x(1−x)ndx equal to ?
View SolutionWhat is ∫10x(1−x)9dx equal to ?
View SolutionWhat is ∫31∣∣1−x4∣∣dx equal to?
View SolutionWhat is ∫eexexdx equal to ?
View Solution