Question

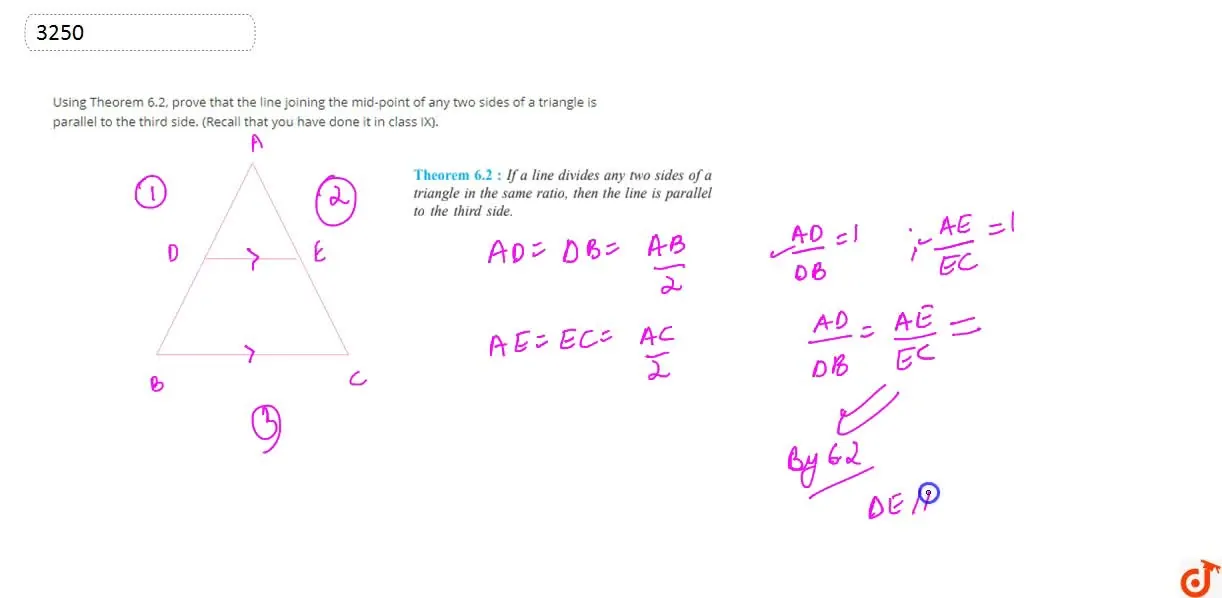
Using Theorem 6.2, prove that the line joining the mid-point of any two sides of a triangle is parallel to the third side. (Recall that you have done it in class IX).

Explanation

To prove that the line joining the midpoints of any two sides of a triangle is parallel to the third side using Theorem 6.2, we can follow these steps:

1. Consider a Triangle: Let triangle ABC be given, where we have points D and E as the midpoints of sides AB and AC, respectively.

2. Identify Midpoints: Since D is the midpoint of AB, we have:
\( AD = DB = \frac{1}{2} AB \)
Similarly, since E is the midpoint of AC, we have:
\( AE = EC = \frac{1}{2} AC \)

3. Set Up Ratios: Now, we can express the ratios of the segments created by the midpoints:
\( \frac{AD}{DB} = \frac{\frac{1}{2} AB}{\frac{1}{2} AB} = 1 \)
and
\( \frac{AE}{EC} = \frac{\frac{1}{2} AC}{\frac{1}{2} AC} = 1 \)

4. Apply Theorem 6.2: According to Theorem 6.2, if a line divides two sides of a triangle in the same ratio, then that line is parallel to the third side. Here, we have:
\( \frac{AD}{DB} = \frac{AE}{EC} = 1 \)
This means that the line segment DE (joining midpoints D and E) divides the sides in the same ratio.

5. Conclude Parallelism: By Theorem 6.2, since DE divides the sides AB and AC in the same ratio, it follows that:
\( DE \parallel BC \)
Thus, we have proved that the line joining the midpoints of any two sides of triangle ABC is parallel to the third side BC.

Final Statement:
Hence, it is proved that the line joining the midpoints of any two sides of a triangle is parallel to the third side.

---