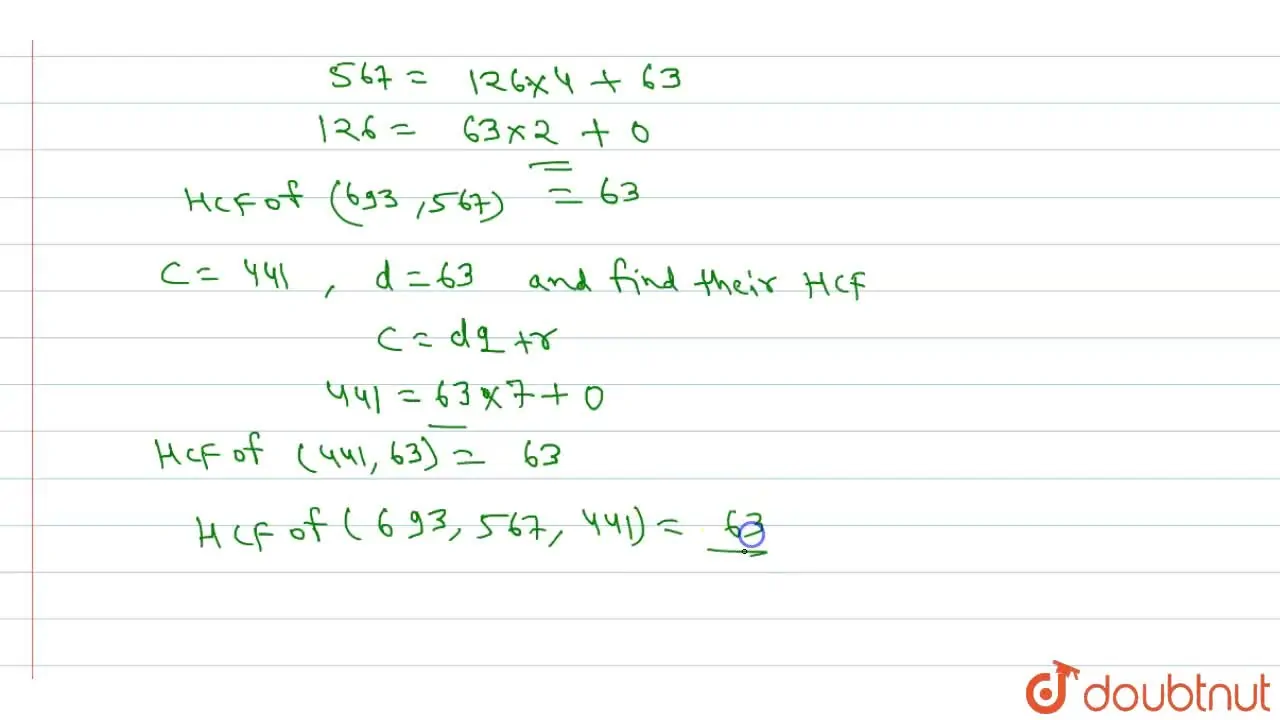Use Euclid division algorithm to find the HCF of 441, 567 and 693.
Video Solution
Text Solution
Let a=693, b=567 and c=441
Euclid's division algorithms, a=bq+r [∴dividend=divisor×quotient+remainder]….(i)
First we take, a=693 and b=567 and their HCF.
693=537×1+126
567=126×4+63
126=63×2+0
HCF (293,567)=63
Now, we take=441 and say d=63 then find their HCF.
Again using Euclid's divison algorithm, c=dq+r
⇒=441=63×7+0
∴HCF(693,567,441)=63
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Use Euclid's division algorithm to find the HCF of 16 and 28.
View SolutionUse Euclid's division algorithm to find the HCF of 455 and 42.
View SolutionUse Euclid's division algorithm to find the HCF of 960 and 432
View SolutionUse Euclid's division algorithm to find the HCF of :
867 and 255View SolutionUse Euclid’s division algorithm to find the HCF of 4052 and 12576.
View SolutionUse Euclid's division algorithm, to find the HCF of 176 and 38220
View SolutionUse Euclid's division algorithm, to find the HCF of 176 and 38220.
View SolutionUse Euclid's division algorithm to find the HCF of :
135 and 225View SolutionUse Euclid’s division algorithm to find the HCF of 210and55.
View SolutionUse Euclid's division algorithm to find the HCFof 210 and 55.
View Solution