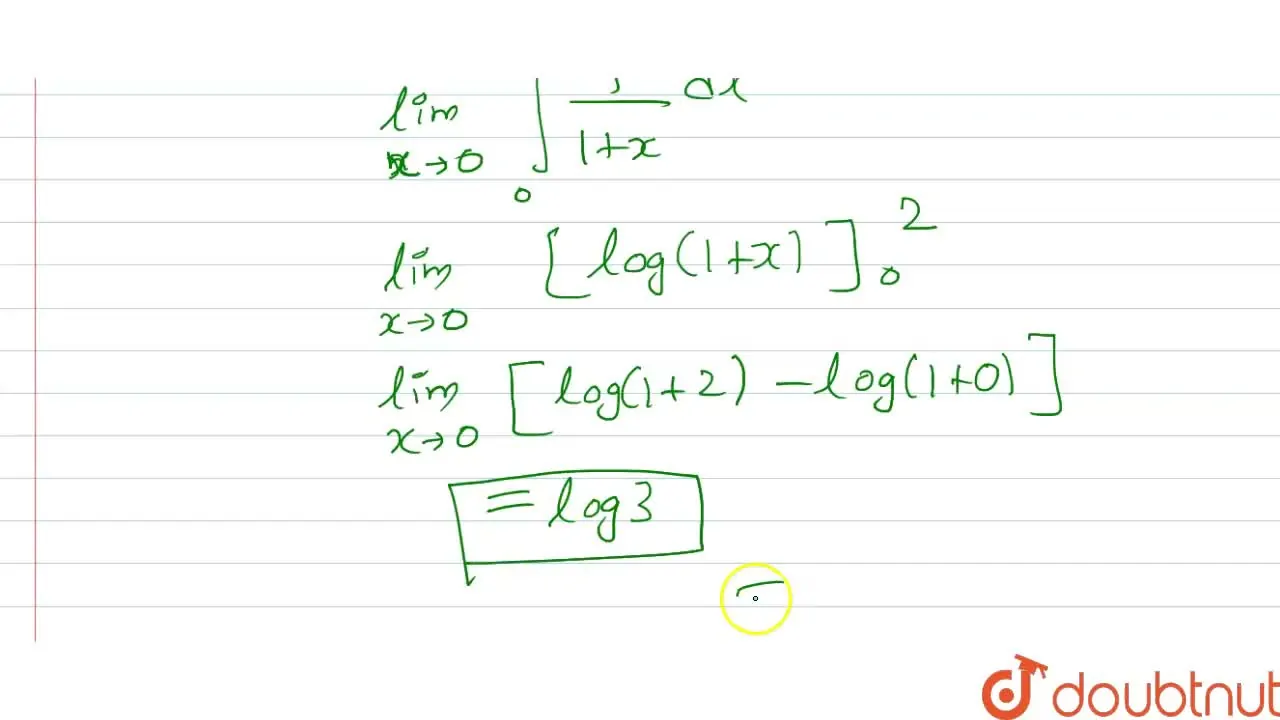limn→∞{1n+1n+1+1n+2+...+13n}=
A
log2
B
log3
C
log5
D
0
Video Solution
Text Solution
The correct Answer is:B
S=limn→∞{1n+1n+1+1n+2+...+13n}
S=limn→∞{1n2n∑r=01n+r}
S=limn→∞{1n2n∑r=0nn+r}=limn→∞{1n2n∑r=011+(r/n)}
Now, Lower limit limn→∞rn
limn→∞rn=0 [∴r=0for the first term]
Upper Limit limn→0rn
limn→∞rn [∴r=2nfor the last term]
∴S=limn→∞{1n2n∑r=011+r(/n)}
⇒S=2∫011+xdx=[log(1+x)]20=log3−log=log3
|
Updated on:21/07/2023
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Section I - Solved Mcqs145videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Section II - Assertion Reason Type12videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise26videos
DERIVATIVE AS A RATE MEASURER
Similar Questions
limn→∞{1n+1+1n+2+1n+3+...+1n+n} is, equal to
View SolutionEvaluate
limn→∞1n[1n+1+2n+2+...+3n4n]View Solutionlimn→∞[1n+1n+1+1n+2+.....+12n]
View Solutionlimn→∞(−1)nnn+1
View Solutionlimn→∞[1n+1+1n+2+…+16n]=
View Solutionlimn→∞(1n+1n+1+...+13n) is equal to
View Solutionlimn→∞[1n+1+1n+2+1n+3+…+12n]=
View Solutionlimn→∞(1n+1+1n+2+1n+3+.........+16n)
View SolutionThe sum S=limn→∞[1n+1+1n+2+1n+3+−−−−−−−−+12n] is equal to ?
View Solutionlimn→∞1n[1n+1+2n+2+....+3n4n]
View Solution